昂尼斯气体绝热过程方程推导及验证＊

杨淑敏 张 伟 麦麦提吐尔逊·努尔麦麦提

（喀什师范学院物理系 新疆 喀什 844000）

目前，在大学物理教材中，大多以范德瓦尔斯气体为例，讨论实际气体的热力学性质.尽管范氏气体方程在一定程度上能够反映气体的实际行为，但是范氏气体方程毕竟也存在对于实际情况的偏离，它也只是从实际气体抽象出来的理想模型.

在描述实际气体时，除范氏气体方程外，还有一些其他形式的非理想气体状态方程，其中最为一般的就是昂尼斯气体方程.描述真实气体状态时，昂尼斯气体方程更为精确，因此研究热力学定律对昂尼斯气体的应用具有一定的意义，国内也有相关文章进行探讨［1～5］.

本文利用热力学第一定律及能态方程推导了昂尼斯气体的绝热过程方程并进行了验证，以使学生加深对实际气体及热力学定律应用的理解.

1 昂尼斯气体绝热过程方程

1.1 昂尼斯气体状态方程

以T，V为独立变量，1mol昂尼斯气体状态方程可表达为

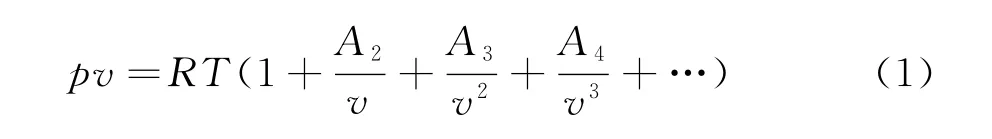
其中v为摩尔体积，A2，A3，A4，… 都是温度的函数，称为第二、三、四 …… 位力系数［6］.

为便于计算，将（1）式改写为

1.2 昂尼斯气体绝热过程方程推导

选取T，V为独立变量，则1mol昂尼斯气体内能可表达为u＝u（T，v），其全微分表达式为

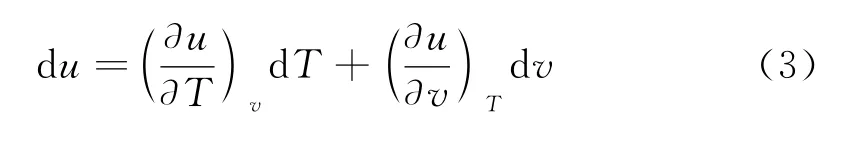
能态方程为

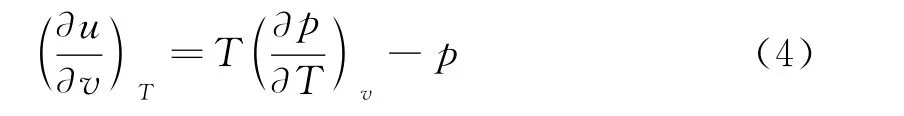
由（2）式可得

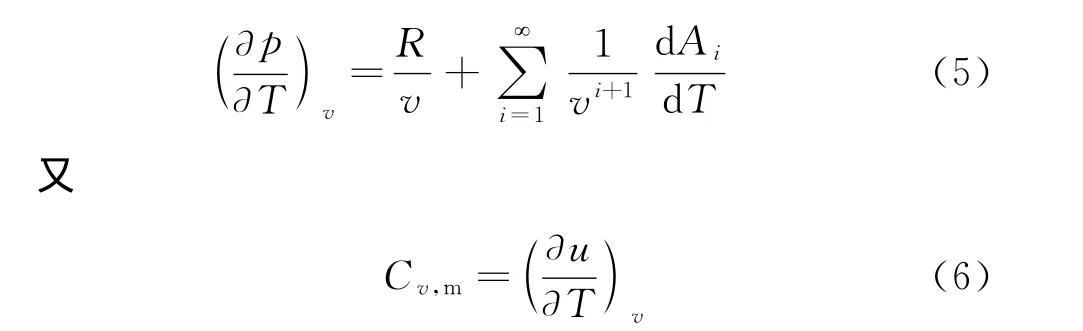
由（3）～ （6）式联立，可得

其中，Cv，m为昂尼斯气体的定体摩尔热容.

根据热力学第一定律du＝dQ＋dW，dW为外界对系统做的功.在绝热过程中dQ＝0，若此时只有体积变化引起的做功，则有

将（2）、（7）式代入（8）式中，可得

化简得

式（9）即为昂尼斯气体绝热过程方程的微分形式.

若在一有限过程中则可利用其积分式

一般来说，Cv，m是温度的函数.但在通常的实际问题中，由于温度变化不大，Cv，m变化很小，因此可视为常量，则（10）式可化为

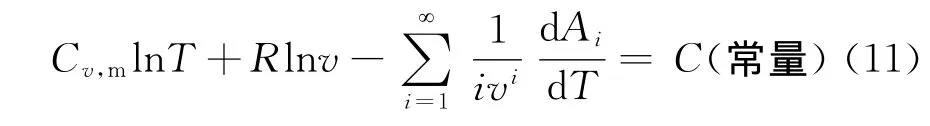
1.3 对理想气体绝热过程的应用

对于理想气体而言，Ai＝0，Cv，m为常量，代入（9）式，得

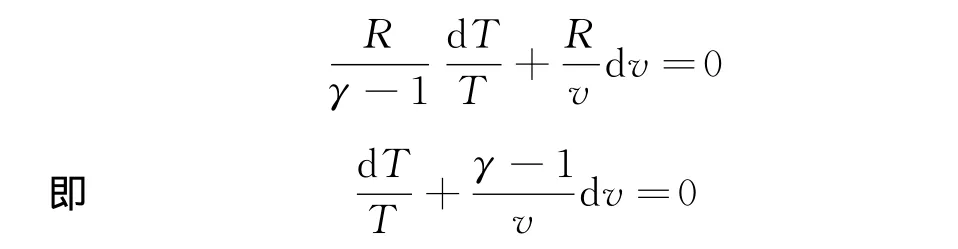
两边积分，得

其中C为积分常量.此即为以温度和体积表达的理想气体绝热过程方程.

1.4 对范氏气体绝热过程方程应用

将（14）式代入（13）式得

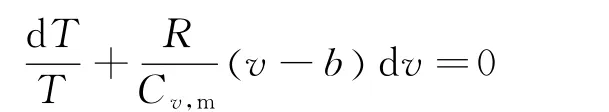
两边积分，得［7］

其中C为积分常量，此即为范氏气体的绝热过程方程.

2 以昂尼斯气体为工质的卡诺循环效率

昂尼斯气体为工质的卡诺循环p-V曲线如图1所示，在整个循环过程中，气体仅在1→2过程中从高温热源T1吸收热量Q1，在3→4过程中向低温热源放出热量Q2，其卡诺循环效率为［4］

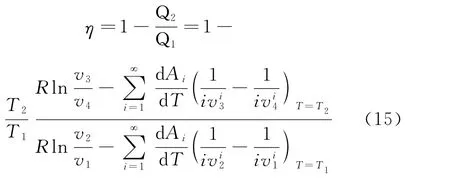
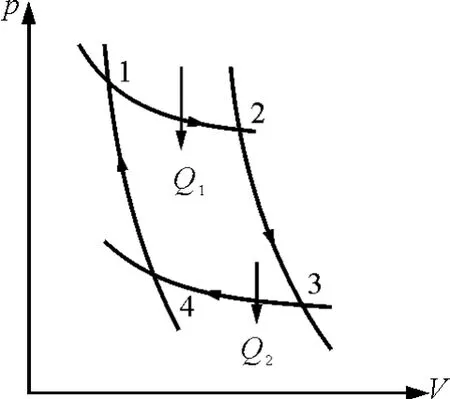
图1 昂尼斯气体卡诺循环p-V图

绝热过程2→3中，由（10）式，得

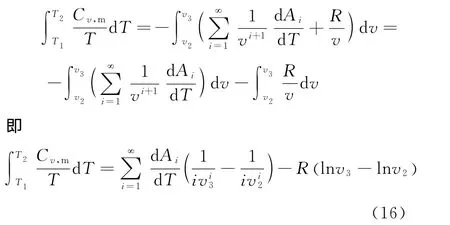
同理，在绝热过程4→1中，有

式（16）、（17）相加，得

将（18）式代入（15）式，可得

即卡诺循环效率.

文献［4］提到，利用可逆循环总熵变为零即可简单求出卡诺循环的效率，上面的运算主要是验证昂尼斯气体绝热方程推导过程的正确性，同时也可作为卡诺定理的一个验证.

3 结论

本文利用热力学第一定律及能态方程进行推导，得到了昂尼斯气体的绝热过程方程较为简洁的形式.在教学过程中，此方程的推导可以使学生加深对实际气体及热力学定律应用的理解.另外，在利用实际气体讨论热机效率时，所涉及的循环过程往往含有绝热过程，因此昂尼斯气体绝热过程方程的推导也具有一定的实际意义.

1 何熙起.昂尼斯气体在任意准静态过程中的摩尔热容.大学物理，2005，24（6）：7～9，19

2 张国文，张拴珠.非理想气体焦耳实验研究.山西师范大学学报（自然科学版），2005，19（2）：40～44

3 王九思.具有长短程相互作用势的一维气体统计力学理论.安徽师范大学学报（自然科学版），1995，18（4）：20～26

4 何熙起.热力学定律对昂尼斯气体的应用.四川师范大学学报（自然科学版），1995，18（1）：49～53

5 符五久.关于昂尼斯方程的讨论.大学物理，1992，11（5）：26，46～47

6 林宗涵.热力学与统计物理学.北京：北京大学出版社，2007.14

7 蓝风华.范德瓦尔斯气体的卡诺循环效率.物理与工程，2011，21（2）：10，26