不愤不启,不悱不发

杨诗鸣

启发性教学原则是最早也是最重要的教学原则. 在我国，最早源于孔子的《论语·述而》：“不愤不启，不悱不发.”它代表着科学、民主的教育思想，使学生更好地掌握知识、发展智力、提高分析和解决问题的能力，同时使学生得到全面发展. 所以，它有着旺盛的生命力，经久弥香.

启发性教学原则如何在课堂上贯穿体现，如何设置数学问题与活动，如何把启发性原则渗透于各种教学手段中，是值得广大教师深入思考的问题，在此笔者结合人教版九年级教材中《圆周角》一课的实际教学案例谈谈体会与经验.

一、引入问题

师：工厂需要生产半圆形零件，利用直角曲尺检验零件的凹面，如何检测可以得到合格的零件？

通过创设情景问题，设置悬念凸现知识落差，激发学生的学习兴趣，从而引入课题.

二、新课讲授

理解圆周角概念：顶点在圆周上，并且两边都和圆相交的角叫做圆周角.

１. 概念的辨析

师：① 你认为概念中有哪些需要注意之处？② 比较圆周角概念与圆心角概念的区别与联系.

生Ａ：顶点位置不同. 生Ｂ：角的大小不同. 生Ｃ：两边都与圆相交. ……

评：师在设疑中应用了以“类比”为目标的启发方法，其特点是学生的认识活动是以确定各种对象或者现象之间在某些特征或关系上的相似为基础的. 与学生已经熟悉的圆心角知识上，通过对与圆心角概念的比较，引导学生寻找类比物的相似属性、现象或性质，训练学生对知识点的迁移与联系的思考. 加深对圆周角两个特征：“顶点在圆上，两边与圆相交”的理解与记忆.

２. 通过实验理解概念

师：让学生自己动手制作圆周角.

生：用图钉把橡皮筋的中间一点固定在圆上一点，再用图钉固定橡皮筋的两边在圆上两点.

师：让学生利用自己制作的圆周角模具讨论回答以下设问：

① 同一条弧所对的圆心角有多少个，圆周角又有多少个？

② 圆心与圆周角有几种不同的位置关系？

③ 若圆心角与圆周角都对着同一条弧，彼此之间是否存在着一定的关系？

生：在圆形纸板上用图钉固定圆上两点，拉动橡皮筋改变顶点位置，分别置于圆心与圆上，观察圆心角与圆周角，研究发现只要与圆的交点不变，圆周角的顶点改变位置就可以出现无数个. 还有学生兴奋地说到：有无数个并且都是相等的. 很快，顺着老师的问题，学生继而发现了，有时圆心在角的内部，有时在角的外部，还会出现在角的边上.

评：此过程应用“操作实验”活动来体现启发性原则，学生通过对相对抽象的数学概念的具体表现形式的操作与观察，实现数学的发现. 同时，学生发现圆心与圆周角的三种位置关系，为后面定理的证明理下非常重要的伏笔.

三、证明定理

１. 创设特殊情景问题

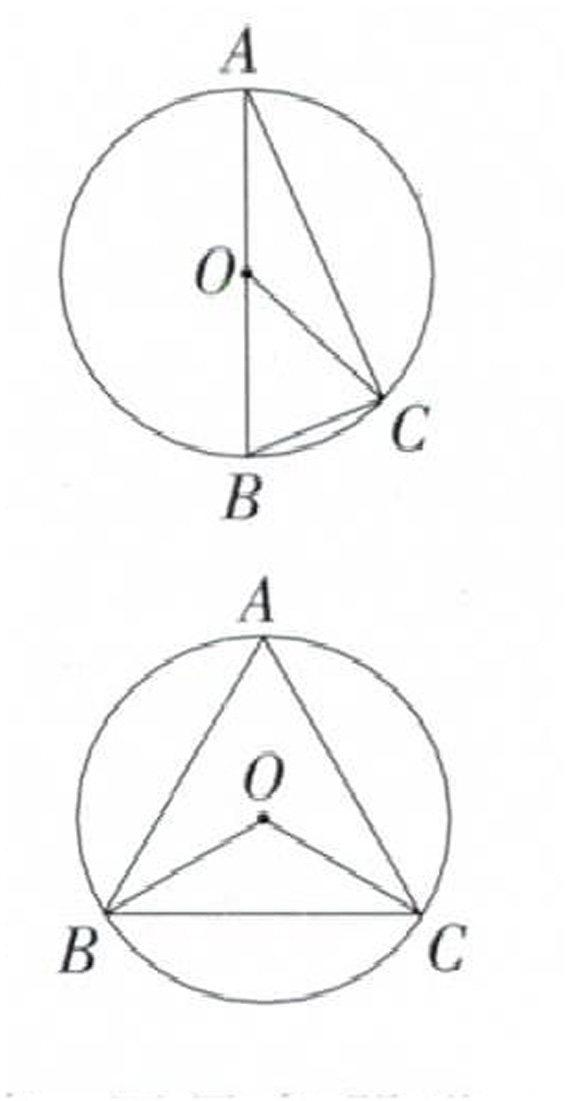
师：① 在⊙Ｏ中，∠A = 30°，∠ACB = 90°，∠BOC = （６０°）。

问：此图中弧ＢＣ所对的圆心角与圆周角有何关系？

② 在⊙Ｏ中，有内接正三角形△ABC，∠BOC =（１２０°）.

问：此图中弧ＢＣ所对的圆心角与圆周角有何关系？

生：通过计算得到答案后，发现圆心角是圆周角的两倍.

２. 归纳结果，提出猜想

师：① 从特殊图形中发现的对着同一弧的圆周角与圆心角的关系是否也存在于一般的图形中？

生：应用自己的模具，找到圆周角与圆心角，用量角器进行大小角度的测量，接着变动顶点与交点的位置，再进行测量. 于是就有学生一边点头，一边低声讨论出自己的猜想.

师：② 教师使用几何画板，拉动顶点位置，让学生观察圆周角与圆心角的大小关系，验证猜想.

评：此过程教师采用引导学生“归纳”的方法体现启发思想，是以归纳过程为支配地位的一种启发方法. 立足学生的认知规律，心理特征与思维方式，采用观察探究的教学法，渗透从特殊到一般的思想方法. 创设特殊的情景问题，作为教学的出发点，从特殊的图形中帮助学生找准知识的连接点，启发学生的思考方向. 同时，此过程也在引导学生进行实验操作过程中实现启发，让学生发挥主观能动性，大胆猜想.

３. 定理的证明

师：① 引导学生根据命题画图，写出已知求证，再由学习小组自行讨论证明.

生：由于有前面探究的基础，学生画图的时候就会出现比较开阔的思路，三种情况都有同学画出，并低声讨论到：应该要分情况讨论才可以.

师：② 对三种情况的证明教师各收集一份展示给同学看，并分别由这三名同学进行讲解. 然后提出：思考：“产生不同证明过程的原因是什么？”从而让学生明白，圆周角与圆心不同的位置关系需要分情况证明.

③ 教师明确指出分情况讨论的必要性与全面性.

评：此过程教师是在“演绎”定理的证明过程中体现启发性原则的，它是以演绎过程为支配地位的一种启发方式. 先指明学生欲要解决的问题，产生自己的问题空间，然后运用数学逻辑和抽象概括进行演绎. 指在渗透完全归纳法和分类思想，让学生充分体会分类讨论的必要性与全面性，才能真正理解此方法，突破此难点.

三、总结

此课例中，教师重组了教材的内容，为实现突破定理证明这个难点，主要在类比、实验、归纳、演绎四种教学活动过程中，体现启发性教学原则的应用，实现对学生学习过程的启发、体现以学生为主体的学习思想；教师不直接地把现成的知识传授给学生，而是引导学生自己独立地发现相应的结果；课堂教学不是教师教学生学，而是通过教师启发、诱导，主要依靠学习者自身的活动来实现教学目标，师生共同活动、民主相处，教学相长；学生不是消极地接受知识，而要靠自己动手、动口、动脑来获得知识；激发学生对知识本身的兴趣，并进一步培养学生对真知的探索和追求；学生在学习的过程中，感受自己的重要性，收获成功的喜悦感.