超精密研抛机床设计

李迎春， 林洁琼， 王 磊， 刘建华

（长春工业大学机电工程学院，吉林长春 130012）

0 引 言

复杂光学曲面涉及非球面和自由曲面等光学曲面，具有十分突出的优越性，不仅在航天航空和国防等领域中有着重要的应用，而且在其它面向消费者的工业领域也将日益受到关注，它既可用于成像光学，也可用于非成像光学［1－3］。在先进光学系统中能否成功地利用非球面及自由曲面光学零件，其关键还在于能否实现非球面及自由曲面零件的高效、高精密、低成本的加工创成。

利用研抛工具的亚口径机械式研抛是目前加工创成复杂光学曲面主要方法，但无论是在创成原理还是在加工装置上，都存在着难以逾越的固有缺陷。目前，许多研究主要是针对回转对称非球面光学零件的加工技术及装备［4－5］。对于有复杂几何特征的光学曲面，研抛去除量总是非均匀变化的，这使得研抛工具与被加工工件之间的变形不一致，难以获得均匀一致的面形精度；研抛工具去除工件材料所形成的加工表面残高也总是非均匀变化的，因而难以获得均匀一致的加工表面质量。为了使所获得加工表面质量和面形精度满足加工要求，同时，机构的设计简单、实用、性能可靠，势必将增加研抛加工时间，降低研抛加工效率［6－8］。

为了克服这些固有缺陷，针对复杂光学曲面的创成，提出一种研抛加工方法以及实现该加工方法的装置。这种复杂光学曲面研抛加工方法，其特征主要在于研抛工具绕z轴作高速回转，可沿x轴和z轴移动；工件沿y轴移动，绕z轴转动，绕y轴摆动；研抛工具相对于工件沿预先获得的非线性螺旋路径运动，并主动调整研抛工具与工件之间的相对姿态，以获得均匀的面形精度和加工表面质量。

1 机床的结构设计

1.1 气浮转台的设计

气浮转台主要包括直流力矩电机、气浮轴承以及轴承所需要的供气系统等组成。气浮转台的各部件在设计时考虑了结构对称性原则，以提高转台轴系回转时的平稳性。转台轴系选用气浮轴承支承，轴系上同轴安装进口无刷直流力矩电机作为直接驱动元件。转台部件在设计制造时力求在形状、尺寸和质量分布上对各自的正交坐标平面对称；并且要求在满足结构件强度和刚度的前提下，同时力求内环轴系质量最小，尽量减小轴系转动惯量。气浮转台利用多孔喷射气浮垫产生静压，支撑待研抛工件。由于采用多孔喷射技术，平台表面压力分布均匀，具有承载能力强、刚度好、抗气振等优点，主要应用于精密测量和超精加工等。精密气浮转台如图1所示。

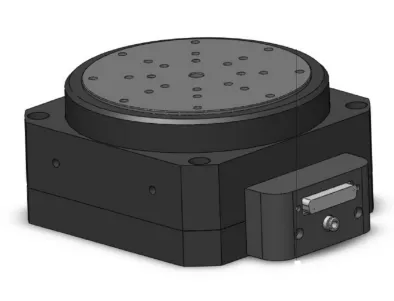
图1 精密气浮转台

气浮转台中的核心部件就是气浮轴承。气浮轴承（又称为空气轴承）指的是用气体（通常是空气，但也有可能是其它气体）作为润滑剂的滑动轴承。空气轴承消除了由摩擦力引起的阻力、磨损，提供了极高的径向和轴向旋转精度。由于旋转的转子和静态支撑部分之间没有机械接触，磨损程度降到了最低，从而确保精度始终保持稳定。空气轴承内部的低剪切力能够在提供极高转速的同时，将动力损失降到最低，使产生的热量非常小，并能同时保持较低的振动水平，在高精度（如μm、亚μm级）、高速领域（如50 000r／min以上）优势十分明显。

1.2 精密摆台设计

精密摆台由直流无刷直驱电机和蜗轮蜗杆构成，在摆动台滑道内的滑块上加工与蜗杆啮合的轮齿，摆台下端的直流无刷电机带动蜗杆的转动，从而控制滑块的滑动。该方案使整体工作方便、可靠；轴系承载能力大，连接刚度高，可达到高的回转精度。由于采用了独特的设计和组合方式，使得转动单元具有高精度、高速度等特点。摆台的摆角范围±20°。精密摆台安装底座上，通过蜗轮蜗杆机构实现微摆动，为此设计制造时要保证底座有足够高的刚度、强度以保证转台各项精度，降低联动造成的交叉耦合力矩等。所设计的精密摆台结构如图2所示。

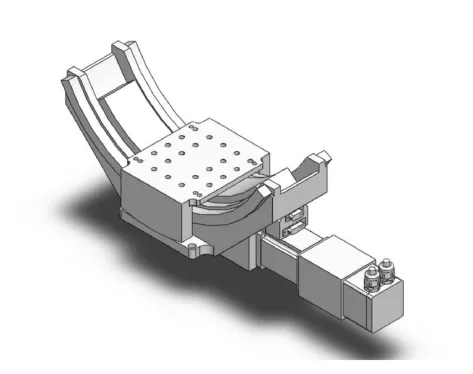
图2 精密摆台

当伺服电机通电后，通过联轴器将扭矩传递给蜗杆。蜗杆固定方式为F-S型，蜗杆固定端由深沟球轴承做径向支撑，由双向推力球轴承锁紧固定端，实现轴向止推。蜗杆自由端由深沟球轴承做径向支撑，并与手动调整旋钮通过键连接。该精密摆台有电动／手动两种驱动方式，通过蜗杆与涡轮齿啮合，实现摆台摆动。

1.3 装配设计

气浮转台和摆台的整体台体结构采用上下式结构，即摆台安装在底座上，摆动角度为±20°；气浮转台通过连接板安装在摆台上，光学元件安装在气浮转台上面，可在摆台处于某位置时绕转台连续旋转360°，具体装配图如图3所示。

图3 气浮转台和摆台的整体装配图

将气浮转台和摆台再装配到机床本体上，得到所设计的超精密研抛机床整体装配如图4所示。

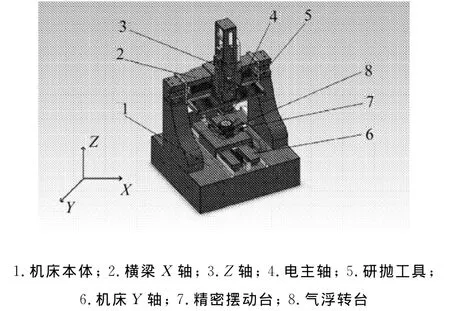
图4 超精密研抛机床总体装配

2 机床关键部件及床身的有限元分析

2.1 精密气浮转台的结构静力分析

将气浮转台三维图形导入ANSYS中，网格单元类型选择Tet 10node 92。气浮转台的网格划分如图5所示。

图5 气浮转台网格划分

设定气浮平台内部最大压强为380 985Pa，则气浮面的极限支撑力为10 572.38N。边界条件设为限制底面的3个自由度，并对顶面施加方向竖直向下的极限均布载荷10 572.38N。最后算出的结构变形图如图6所示。

图6 气浮转台结构变形图

由图6可知，气浮转台的最大变形量为4.18 ×10－5mm，远小于超精密机床的技术指标要求。所设计的气浮转台刚度完全可以保证精密加工时的精度要求。

2.2 精密气浮摆台的结构静力分析

2.2.1 有限元模型的建立

在CATIA中建立几何模型，然后导入ANSYS，单元类型选择SOLID186，材料模型定义参数：EX为7.0E10，PREX为0.3，DENS为2.85E3，对模型划分网格。划分网格后的模型如图7所示。

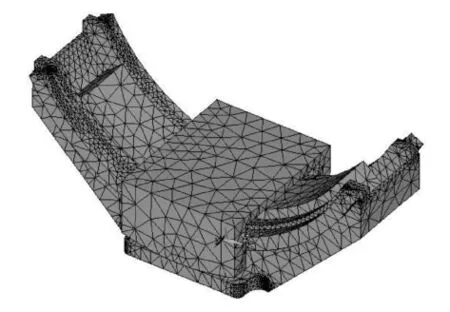
图7 精密摆台网格图

2.2.2 加载及求解

边界条件设为限制底面位移的3个自由度，并对顶面施加方向竖直向下的极限均布载荷，运行Solution中的Solve命令进行求解。

2.2.3 结果分析

变形量为3.47×10－8mm，该变形量完全可以保证精密加工时的精度要求，因此精密摆台的设计满足要求。精密摆台的变形情况如图8所示。

图8 精密摆台变形图

2.3 研抛机床床身的有限元分析

建立机床床身的几何模型，选择单元类型为SOLID92，材料模型参数定义为：弹性模量EX为1.0E11，泊松比PREX为0.3，密度DENS为7.3E3，整个研抛机床床身的近似模型和有限元网格模型如图9和图10所示。

图9 研抛机床床身模型

图10 研抛机床床身有限元网格模型

2.3.1 横梁的静力分析

首先对横梁在加载集中载荷和加载分布载荷两种情况下进行静力分析，求出最大变形量，并分析其对加工精度的影响。

2.3.1.1 加载及求解

由于研抛机床横梁两端固定在立柱上，所以，两端与立柱接触部分的节点全部自由度均受约束。横梁除了受自重载荷，还受到研抛工具和Z轴部件重力负载。由于只研究梁的最大变形量，故将集中载荷或均布载荷加载在横梁上，运行Solution中的Solve命令进行求解。

2.3.1.2 结果分析

两种不同载荷情况下研抛机床横梁的变形如图11所示。

图11 横梁的变形图

由图11可知，研抛机床横梁在集中载荷和均布载荷的最大变形分别为5.13×10－7mm和6.68×10－8mm，对研抛机床精度影响都不大。

2.3.2 床身模态分析

模态是机械结构的固有振动特性，每一个模态具有特定的固有频率、阻尼比和模态振型。文中对设计的研抛机床的床身进行模态分析，研究研抛机床的固有频率和振型。

2.3.2.1 加载及求解

在加载之前首先应声明结构分析类型，此处定为模态分析（Modal）。文中选择BlockLanczos法进行模态分析，模态分析阶数为6阶。直接在底板面加全约束，限制所有的自由度，与机床的实际约束相符合。运行Solve进行求解，得到机床的前6阶固有频率以及振型图。

2.3.2.2 结果分析

经过有限元分析得到的研抛机床前6阶模态如图12所示。

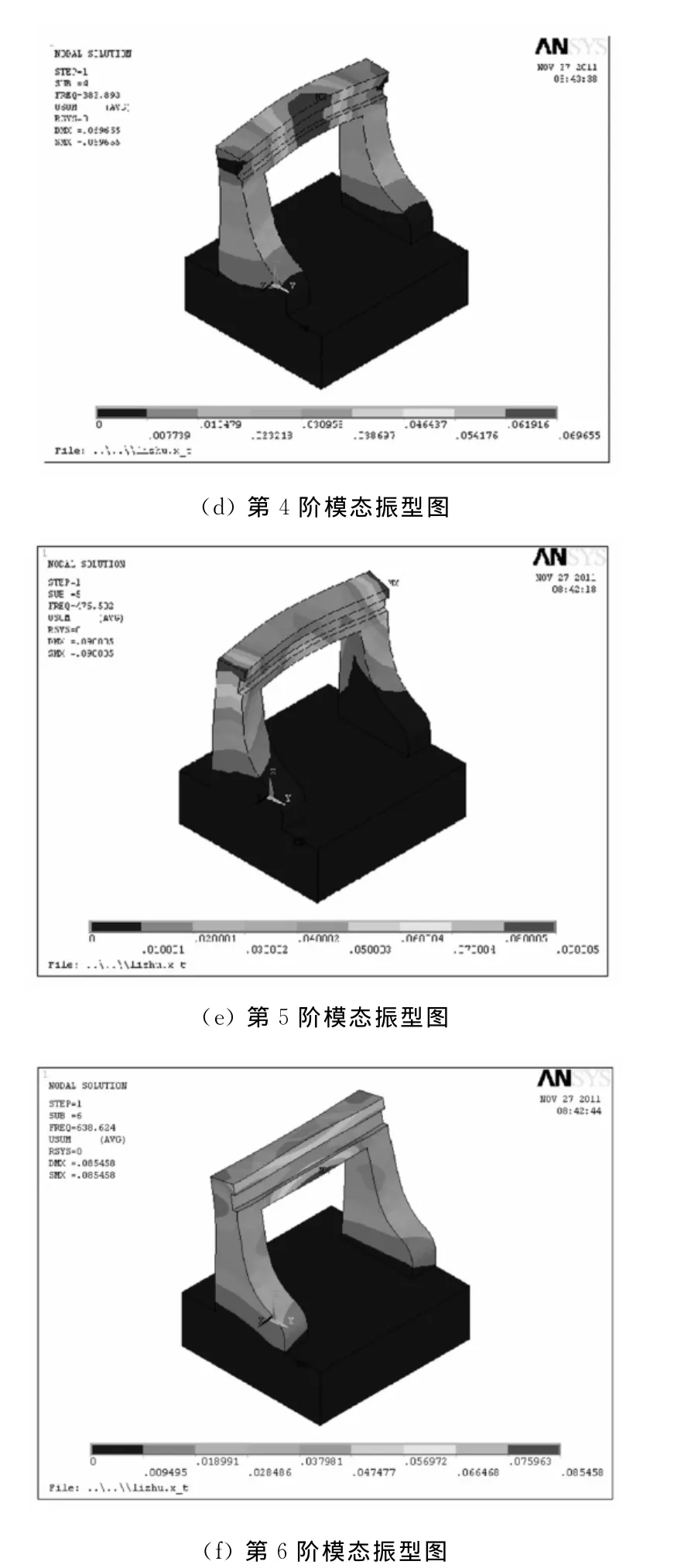
图12 研抛机床前6阶模态

所得到的固有频率结果如图13所示。

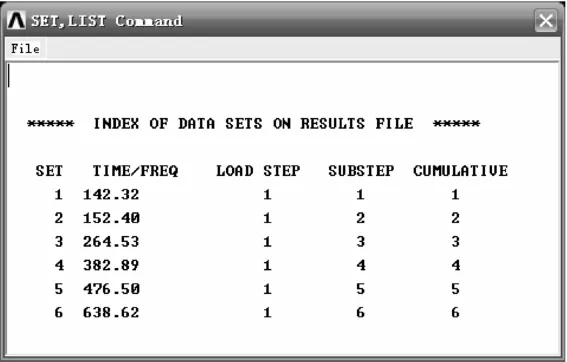
图13 研抛机床前6阶模态固有频率结果

研抛机床的固有频率和床身的固有频率基本相近，故可认为研抛机床的固有频率近似等于床身的固有频率。受到振动影响主要是研抛工具工作时的振动引起的，设计的研抛工具的最大转速为3 000r／min。根据如下公式计算研抛机床的工作频率：

式中：f——研抛机床的工作频率；

n——研抛工具的主轴转速。

当研抛机床工作时，频率为50Hz，与研抛机床的固有频率相差较大，故不会引起共振，即设计的研抛机床合理。

3 结 语

通过有限元分析软件ANSYS对研抛机床关键部件进行静力分析和模态分析可知，文中设计的超精密研抛机床整体结构符合要求。同时，机床也能够达到高效、高精密、低成本加工创成非球面及自由曲面零件的要求，具有十分广泛的应用前景。

［1］ Cvetkovic A，Dross O，Chaves J，et al.Etenduepreserving mixing and projection optics for high-lu-minance LEDs applied to automotive headlamps［J］.Optics Express，2006，14（26）：13014-13020.

［2］ Plummer W T.Free-form optical components in some early commercial products［C］／／Proceedings of the ASPE Winter Tropical Meeting on Freeform Optics.Chapel Hill：［s.n.］，2004：68-71.

［3］ Ott P，Pogany P.Optical design of head-up displays using CAD-compatible freeform surfaces［J］. Photonik International，2009（1）：42-45.

［4］ Bingham R G，Walker D D.A novel automated process for aspheric surfaces［J］.Proceedings of the SPIE，2000，4093：445-450.

［5］ Ruckman J，Fess E，Van Gee D.Recent advances in aspheric and conformal grinding at the center for optics manufacturing［J］.Proceedings of the SPIE，1999，3782：2-10.

［6］ 刘春阳，勾志践.六方体机械万向调节机构的设计与应用［J］.长春工业大学学报：自然科学版，2007，28（1）：118-120.

［7］ Ludwick S J.A rotary fast tool servo for diamond turning of asymmetric optics［D］：［PhD thesis］. Adviser：Trumper，Massachusetts Institute of Technology，1999.

［8］ Tomhe Y，Lowe J A.Machining of freeform optical surfaces by slow slide servo method［C］／／Proceedings of the 18th ASPE Annual Meeting.2003.