捕食模型反应扩散方程组的有限差分法

周 丽

（安徽农业大学理学院，安徽合肥 230031）

0 引 言

在文献［1］中，作者讨论了捕食模型的反应扩散方程组：的解的动力学性质。

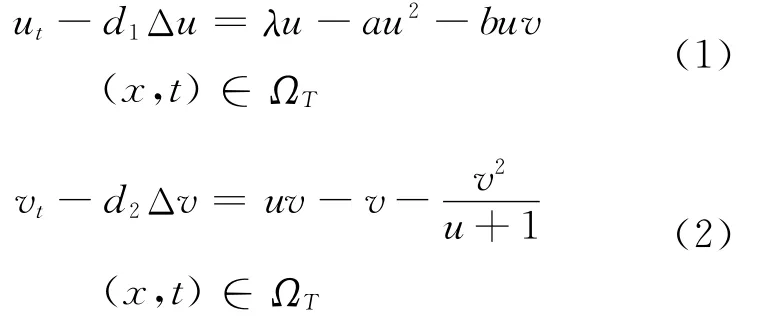
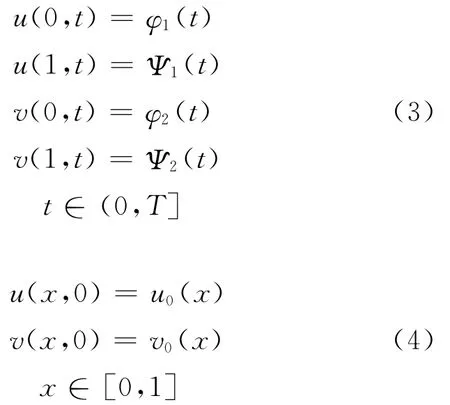
文献［2-3］分别对三级食物链反应扩散模型和具有有限时滞的种群扩散方程进行了定性分析，由于生物学中大多数现实模型都是非线性而无法求解析解的，因此，数值求解对研究解的性态就显得尤为重要。有限差分法和有限元法被广泛用于求这类问题的数值解，文献［4］对反应扩散方程构造了交替差分格式，并证明了格式的无条件稳定性，文献［5］对非线性反应扩散方程组建立了二阶收敛的三层线性化差分格式，文献［6］对反应扩散方程组的Stefan问题建立了二阶收敛的两层线差分格式，文献［7］对λ－ω型的反应扩散方程组利用有限元法求得了近似解。文中给出方程组（1）～方程组（4）的一个二层线性化差分格式，并给出解的存在唯一性、收敛性和无条件稳定性的证明。

文中假设：方程组（1）～方程组（4）存在唯一解（u，v）∈C4，3（ΩT），且存在常数C0＞0，使得u，v及其导数以C0为界。

以下记

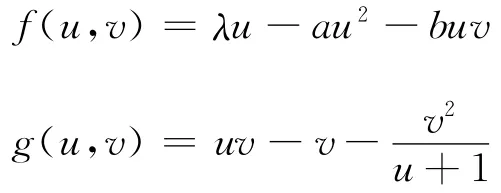
则由上述假设可知存在常数C1，使得当｜u｜，｜v｜≤C0＋1时，f（u，v），g（u，v）及其二阶导数以C1为界。

1 差分格式的建立

取正整数m，n，记

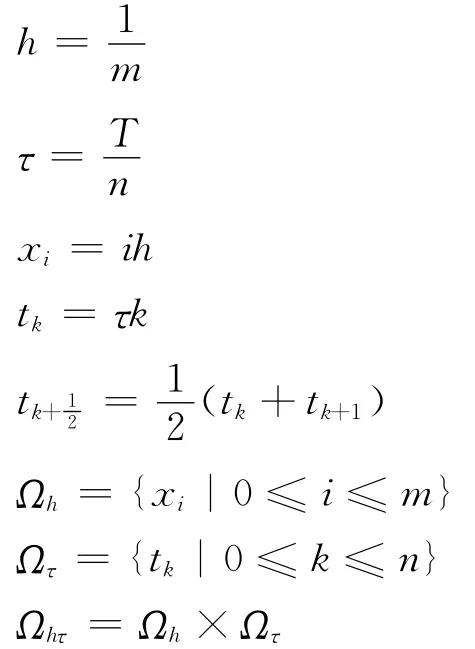
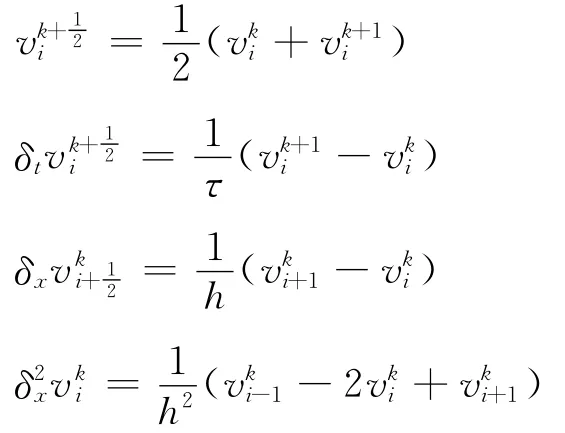
定义Ωhτ上的网格函数

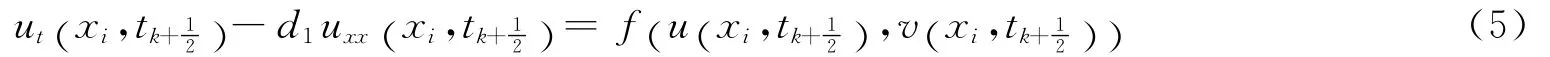
由Taylor展开可得

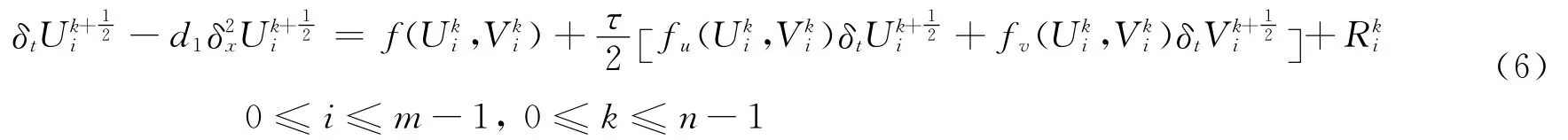
且存在常数CR使得

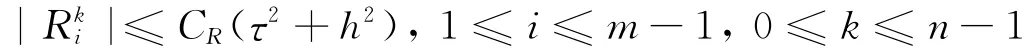
同理，由方程（2）得

且存在常数~CR使得

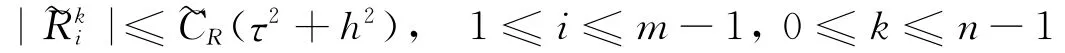
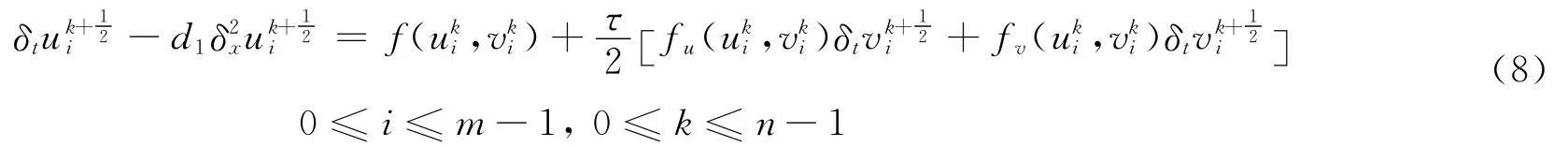
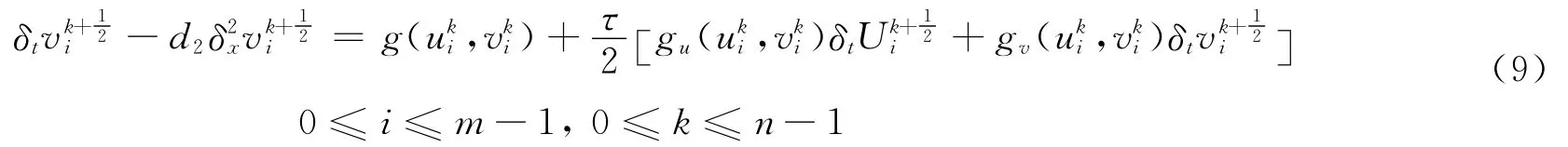
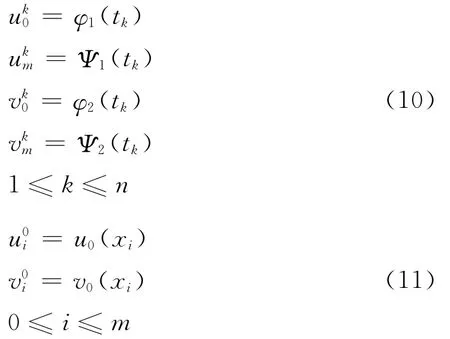
2 差分格式的可解性收敛性和稳定性

记Vh＝｛ω｜ω＝｛ωi，0≤i≤m｝为Ωh上的网格函数，且ω0＝ωn＝0｝。设ω∈Vh，记

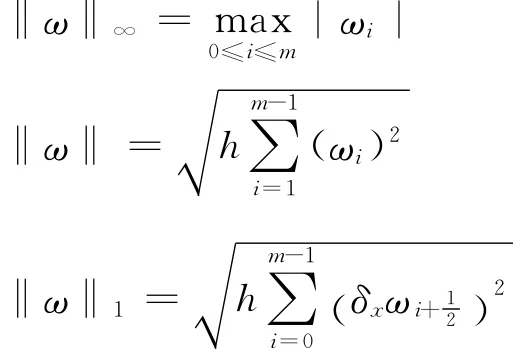
引理1［8］设v，ω∈Vh，则有

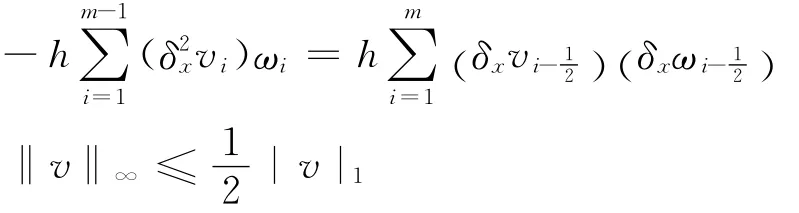
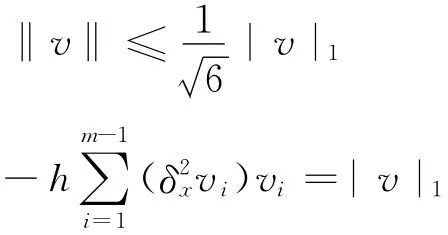
定理1 1）当h，τ适当小时，差分格式（8）～（11）存在唯一解。2）设｛u（xi，tk），v（xi，tk）｜0≤i≤m，0≤k≤n｝是问题（1）～（4）的解，｛（uki，vki）｜0≤i≤m，0≤k≤n｝是差分格式（8）～（11）的解。记

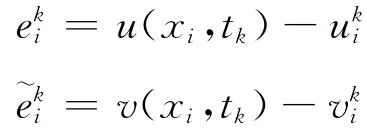
则当h，τ充分小时，有

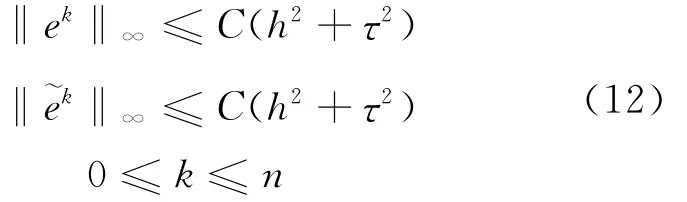
其中

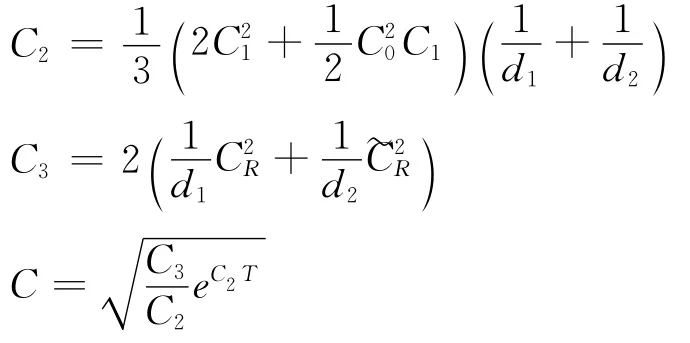
证明 差分格式（8）～（11）的误差方程如下：

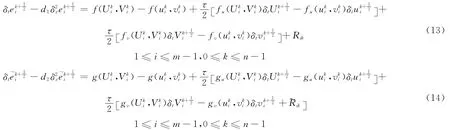
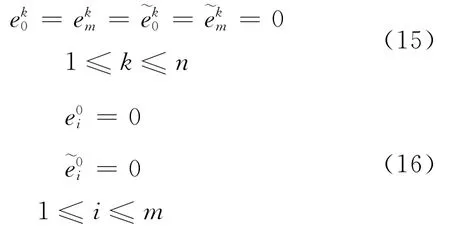
下面用归纳法证明差分格式（8）～（11）是唯一可解的，且式（12）成立。

当k＝0时，由式（11）知

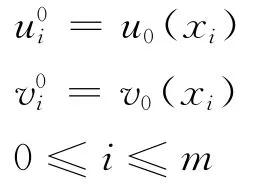
因此，u0，v0唯一确定。

由式（16）知

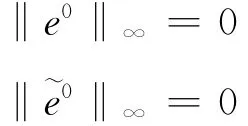
因而结论对k＝0成立。

现假设当0≤k≤l时差分格式（8）～（11）唯一确定出uk，vk，且式（12）对0≤k≤l成立。于是当h，τ适当小时

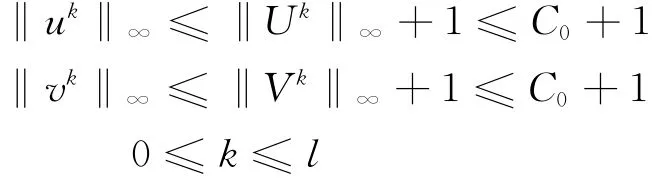
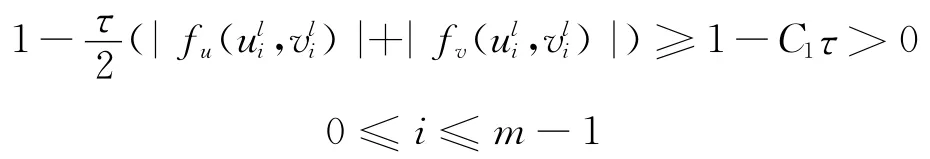
下面证明估计式（12）对k＝l＋1也成立。

由

知

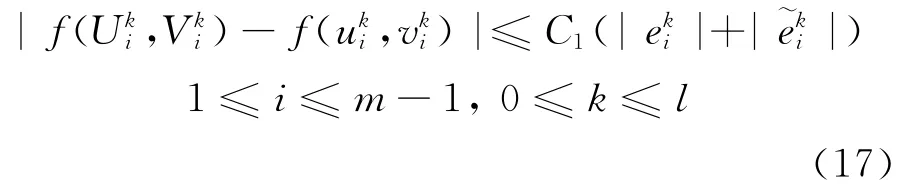
由

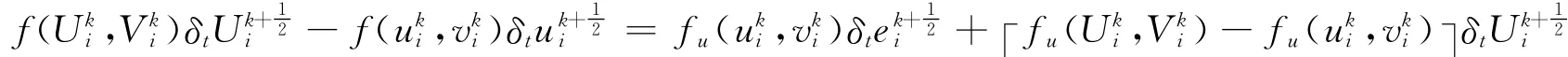
知

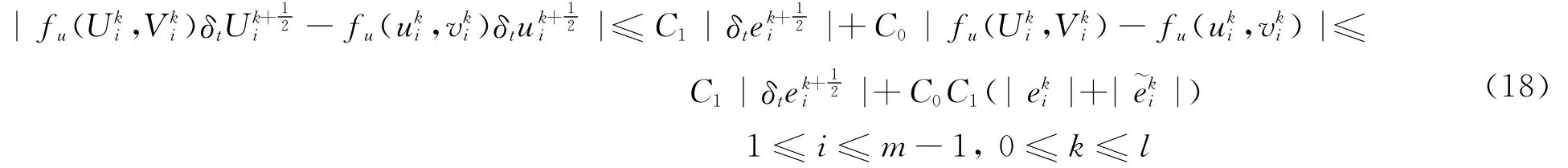
同理

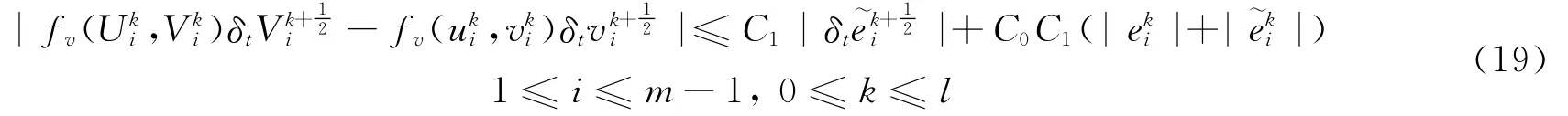
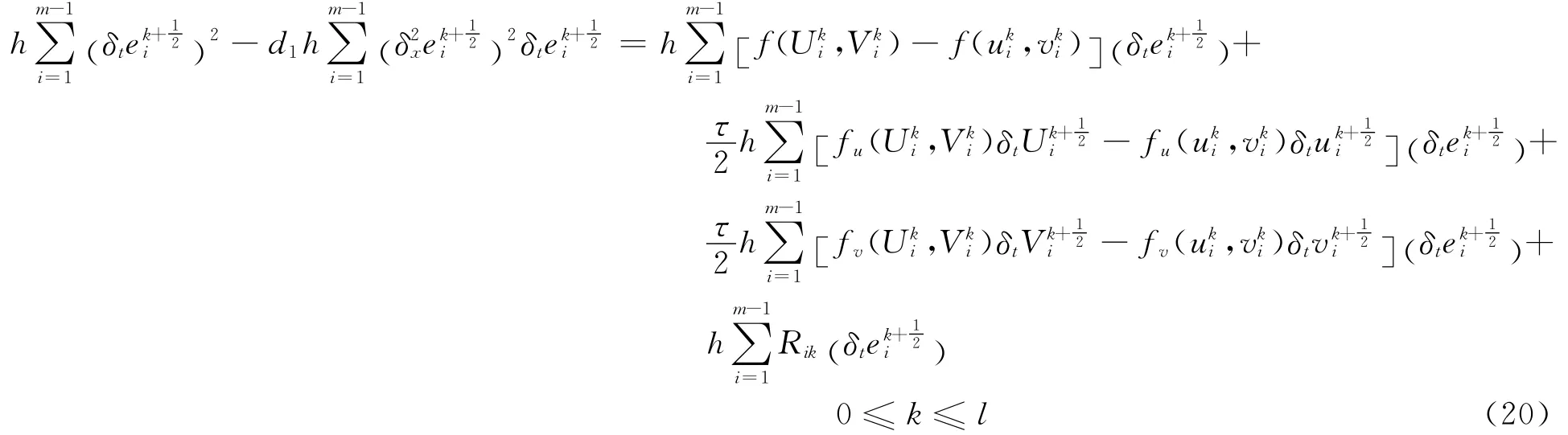
将式（17）～式（19）代入式（20），并应用引理可得

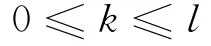
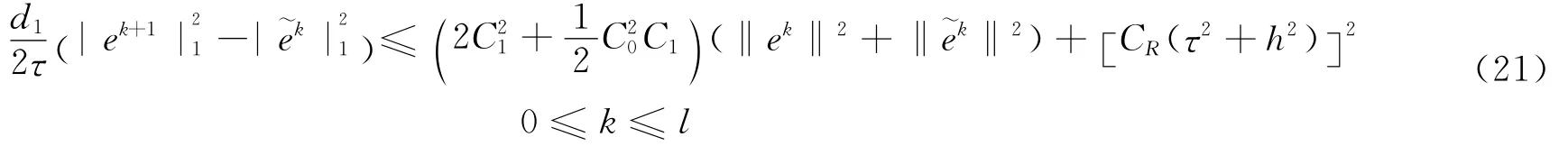
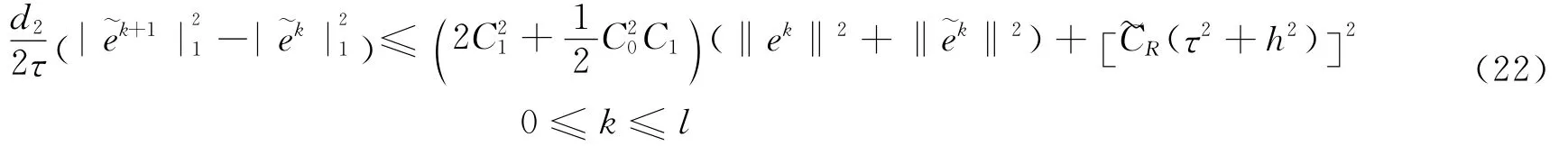
将式（21）除以d1，式（22）除以d2，并将所得结果相加，再应用引理得到

即

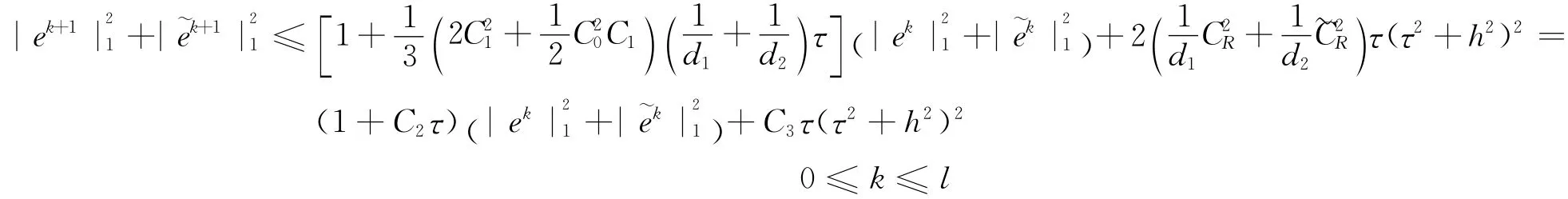
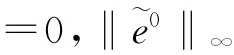
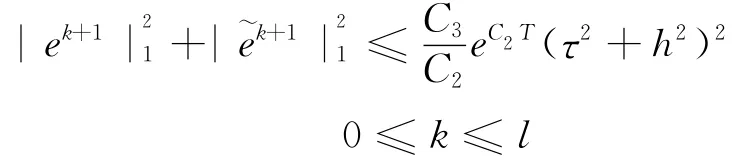
因而

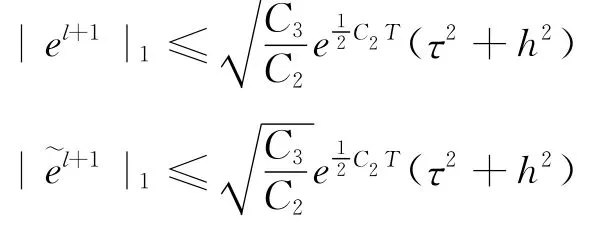
应用引理，易得

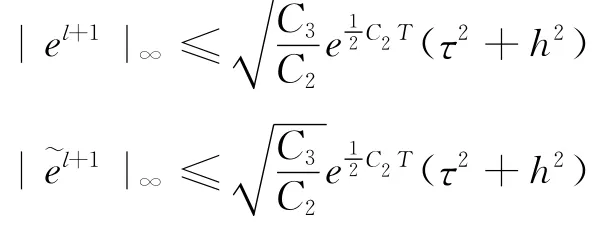
即式（12）对k＝l＋1成立，由归纳假设法，命题得证。

现在讨论差分方程（8）～方程（11）关于初值的稳定性。

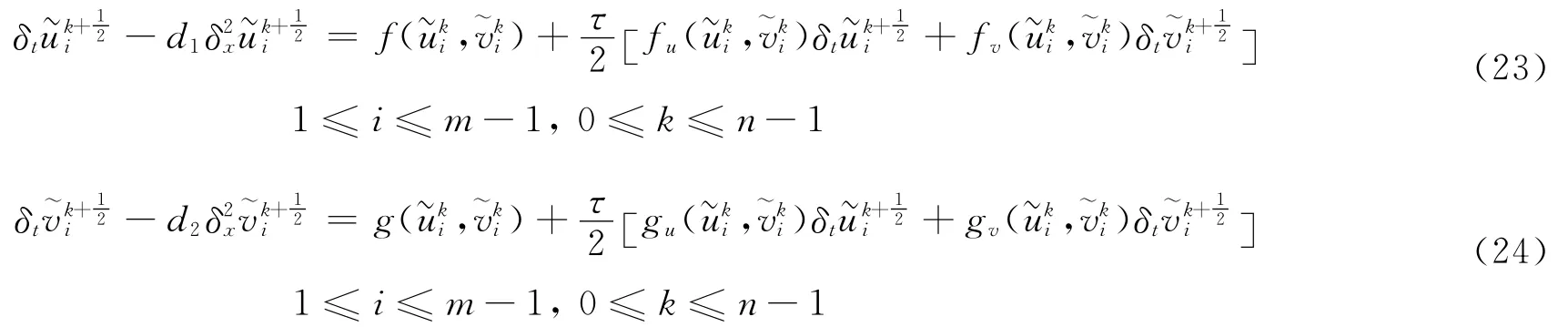
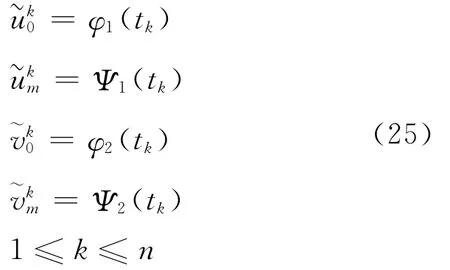
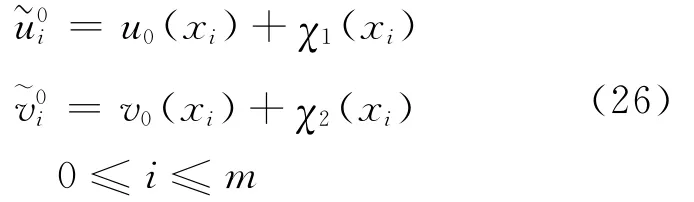
记

将式（23）～式（26）分别和式（8）～式（11）相减得：

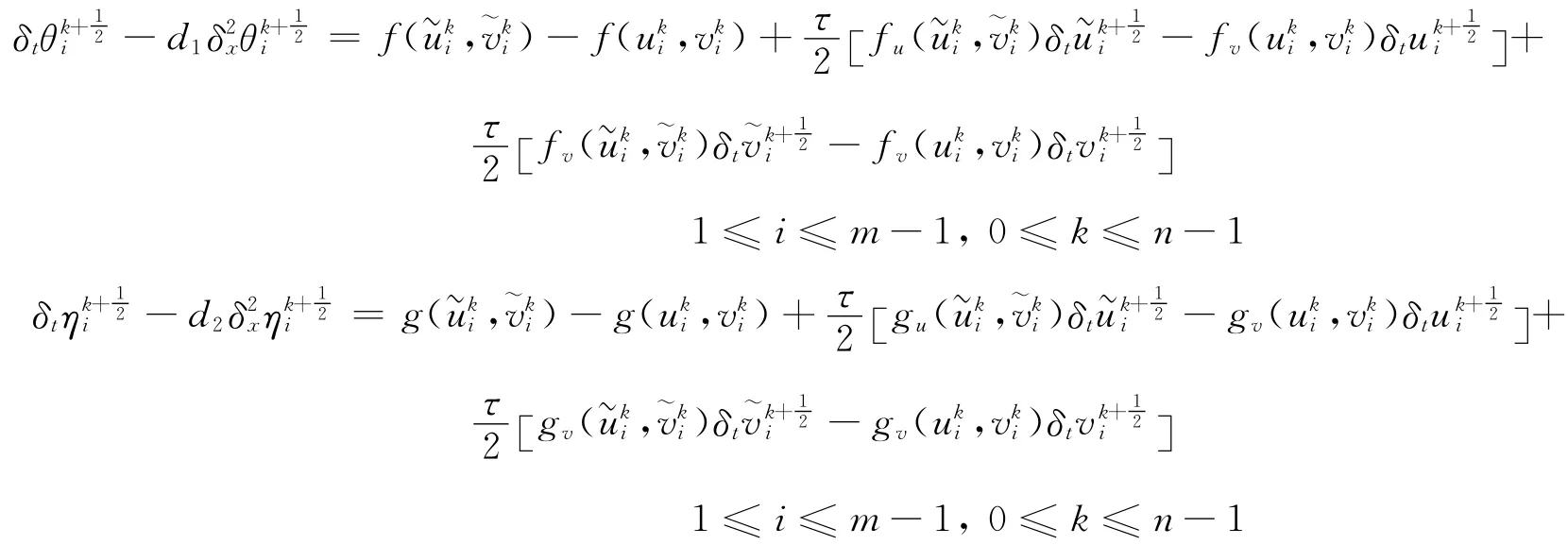
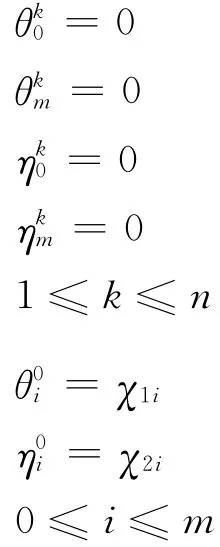
类似于定理1的讨论，可得下面稳定性的结论。

定理2 当h，τ充分小时，存在常数C，有

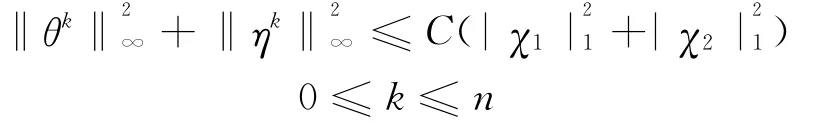
3 结 语

对生物学中提出的一类半线性抛物方程组建立了一个两层线性化差分格式。证明了所构造的差分格式是唯一可解的、收敛的，且是稳定的。

［1］ 郁莉莉.一个捕食模型的的反应扩散方程组解的动力学性质［J］.淮海工学院学报：自然科学版，2010， 19（2）：1-3.

［2］ 陈文彦，王明新.一个与比值有关的三级食物链反应扩散模型的定性分析［J］.江苏大学学报：自然科学版，2004，25（2）：137-140.

［3］ 王健，岳锡亭，王雪.具有时滞种群发展方程的稳定性区域判定［J］.长春工业大学学报：自然科学版，2011，32（5）：489-493.

［4］ Yuan Guang-wei，Shen Long－jun，Zhou Yu-lin. Unconditional stablility of parallel alternating difference schemes for semilinear parabolic systems［J］.Appl.Math.Comput.，2001，117：267-283.

［5］ Zhang Ling-Yun，Sun Zhi-Zhong.A second-order linearized difference scheme on nonuiform meshes for nonlinear parabolic systems with Dirichlet boundary value conditions［J］.Numer Meth.Partial Differential Eqs.，2003，19：638-652.

［6］ Khaled Omrani.On the numerical approach of the enthalpy method for the stefan problem［J］.Numer Methods Partial Differential Eq，2004，20：527-548.

［7］ James F Blowey，Marcus R Garvie.A reaction-diffusion system ofλ－ωtype Part I：Mathematical analysis［J］.Applied Mathematics，2005，15：1-19.

［8］ 孙志忠.偏微分方程数值解［M］.北京：科学出版社，2004：8-9.