基于机器加工时间最短的混合遗传算法

王 威， 徐 兵， 岳晓峰

（长春工业大学机电工程学院，吉林长春 130012）

0 引 言

车间作业调度问题（Job Shop Problem，JSP）是最困难的组合优化问题之一。近年来，基于概率搜索方法的发展为求解车间作业调度问题带来了巨大推动，它已经成为解决该类问题的有效方法之一，如模拟退火（Simulation Anneal，SA）、禁忌搜索（Taboo Search）、遗传算法（Genetic Algorithm，GA）［1］。它们在求解时最大的特点是以概率的方式搜索问题的解空间，并通过目标函数的评价，使搜索过程不断收敛于一个值上。然而，单独使用标准遗传算法解决车间调度问题时，效果往往不理想［2］。这是因为标准遗传算法是一种通用的优化算法，采用它来解决调度方案时，必须与调度本身的一些特点结合，如调度产生时必须满足加工工艺等约束条件，指导迭代的搜索方向，而且企业的调度问题比较复杂，在实际的调度问题中，往往是零件与可加工机器之间存在一对多的情况，为了确定机器与工件的关系，文中提出了一种混合式遗传算法，它在遗传算法中嵌入了基于机器加工时间最短为策略的启发式方法，从局部和全局引导遗传算法的搜索方向，提高了算法的效率，并且实例考证了HGA算法在解决某军工企业生产调度问题时的有效性［3－4］。

1 GA模块

1.1 编码

文中采用了基于工件的编码方式。编码问题是设计遗传算法的首要和关键问题。遗传算法必须要考虑“染色体”的合法性、可行性、有效性以及对问题解空间表征的完全性，求解JSP同样如此。鉴于JSP的组合特性以及工艺约束性，染色体的Lamarkian特性、解码的复杂性、编码空间特性和存储量的需求是设计遗传算法编码时需要考虑的问题。由于二进制编码方式存在着不能直接反应所求问题的结构特征，不便于开发针对问题的专门知识的遗传算子，同时也很难满足积木块儿编码原则等的诸多缺点［5］。采用简单的二进制串编码方式已不能有效地解决JSP问题。文中根据问题特点采用基于工件的编码方式。这样编码的好处是染色体Lamarkian性，并且通过简单的映射关系就能实现解码的相应编码，任意工件的置换排列均能表示可行调度，编码长度也远小于二进制的编码方式。

1.2 遗传算子

1.2.1 选择算子

采用赌轮法进行选择。由于赌轮选择的非负性要求，以及为了提高个体之间的差异性，文中采用了sigma truncation的缩放方法来确定个体的适应值，其公式为［6］：

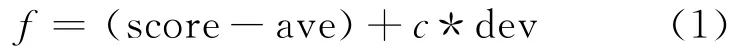
式中：score——个体的原目标函数值；

ave——种群的均值；

dev——种群的方差。

1.2.2 交叉算子

文中交叉策略采用部分匹配法，该方法是不直接进行两个父代之间的交叉，而是两子代分别依据各自的父代，通过交换自己相应位置的基因而实现相对意义上的交叉，这种方式的好处在于不会产生非法解，从而免去非法解的过程，提高了程序的运行效率［7］。

1.2.3 变异算子

为保证种群的多样性以及使算法能在更广阔的可行解空间中搜索最优解，同时为了防止程序陷入局部最优解的瓶颈，文中采用了如下方法：随机得出两个点后，将两点之间的基因按概率进行互换，这样既保证了个体的多样性，同时又保留了部分基因，使得程序免于因变异随机性太大而影响程序的收敛［8］。

1.3 混合遗传算法的过程描述

步骤1：生成初始种群。采用基于工件的编码方式进行编码。

步骤2：计算适应值。采用sigma truncation的缩放方法来确定个体的适应值。

步骤3：判断是否达到迭代次数或者遗传是否趋于稳定。如果达到，则输出最优调度解，并退出；否则进行步骤4。

步骤4：遗传操作。

1）依据前述的选择策略选择出要交叉的父代个体。

2）依据交叉概率来确定两个父代是否需要交叉，若需要则采用部分匹配法进行交叉，否则直接将两父代复制给下一代。

3）变异操作。

4）转步骤3，看是否满足终止条件，满足则终止；否者返回步骤2。

2 基于混合遗传算法求某军工企业柔性制造车间一期工程的生产调度

文中以某军工企业柔性制造车间一期工程的生产任务为例，在Visual C＋＋6.0上实现的混合遗传算法，以验证其有效性，并与用标准遗传算法产生的结果进行比较［9］。

2.1 实例

种群规模为40，交叉概率为0.9，变异概率为0.01。

在算法设计上，将该军工企业一期工程所有要加工的13种工件按照顺序依次确定1～13，给出的11台机器也是按其标号来确定的，见表1。

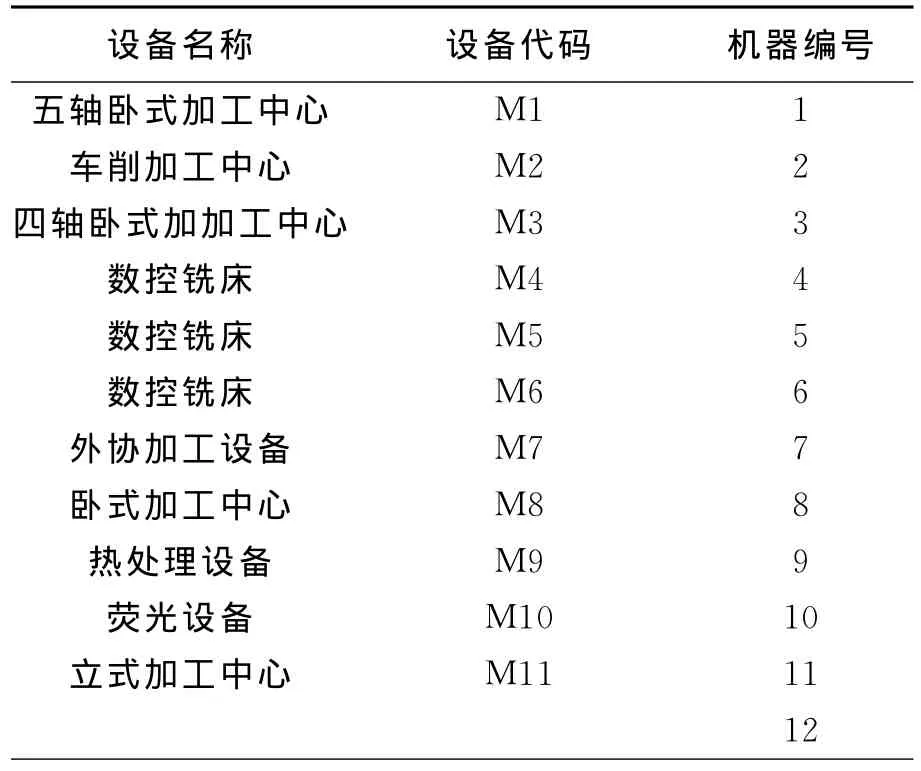
表1 加工机器及编号详细表

续表1

其中，机器编号12表示工件可能的加工机床“M1，M2，M3，M4，M5，M6，M8，M10”，13表示工件可能的加工机床“M1，M3，M8”，14表示工件可能的加工机床“M2，M3”，15表示工件可能的加工机床“M1，M3”，16表示工件可能的加工机床“M2，M3，M11”，17表示工件可能的加工机床“M3，M8”。

工件的机器顺序矩阵见表2。

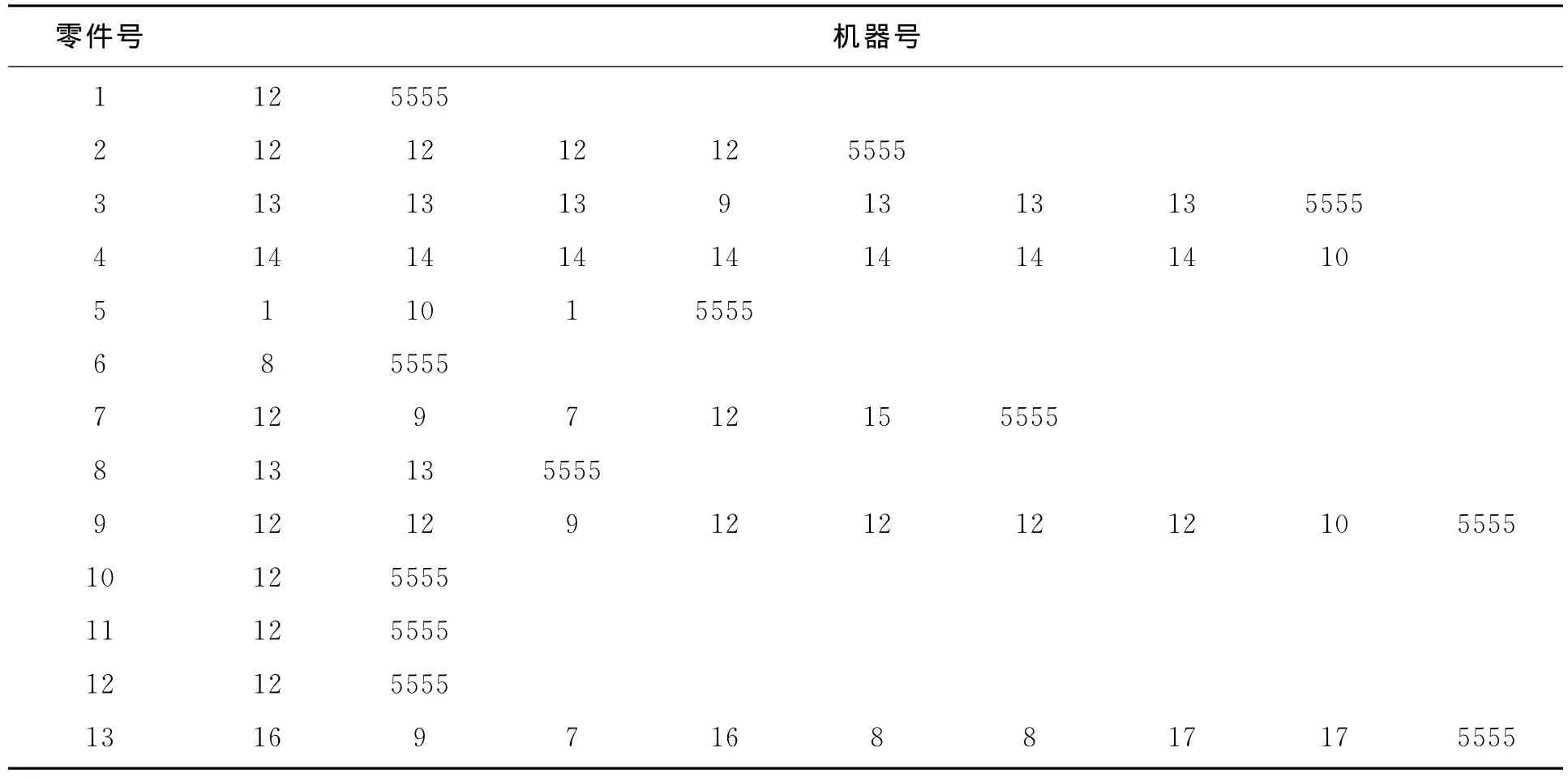
表2 工件的机器顺序矩阵

表2是工件的机器顺序矩阵，其存储在txt格式的文件中，这样的好处是在机器或者零件发生变动时便于改动数据。一旦程序运行，就会从文件中读取数据，并存储在相应的机器矩阵中。“5555”是换行标志。

工件的加工时间矩阵见表3。

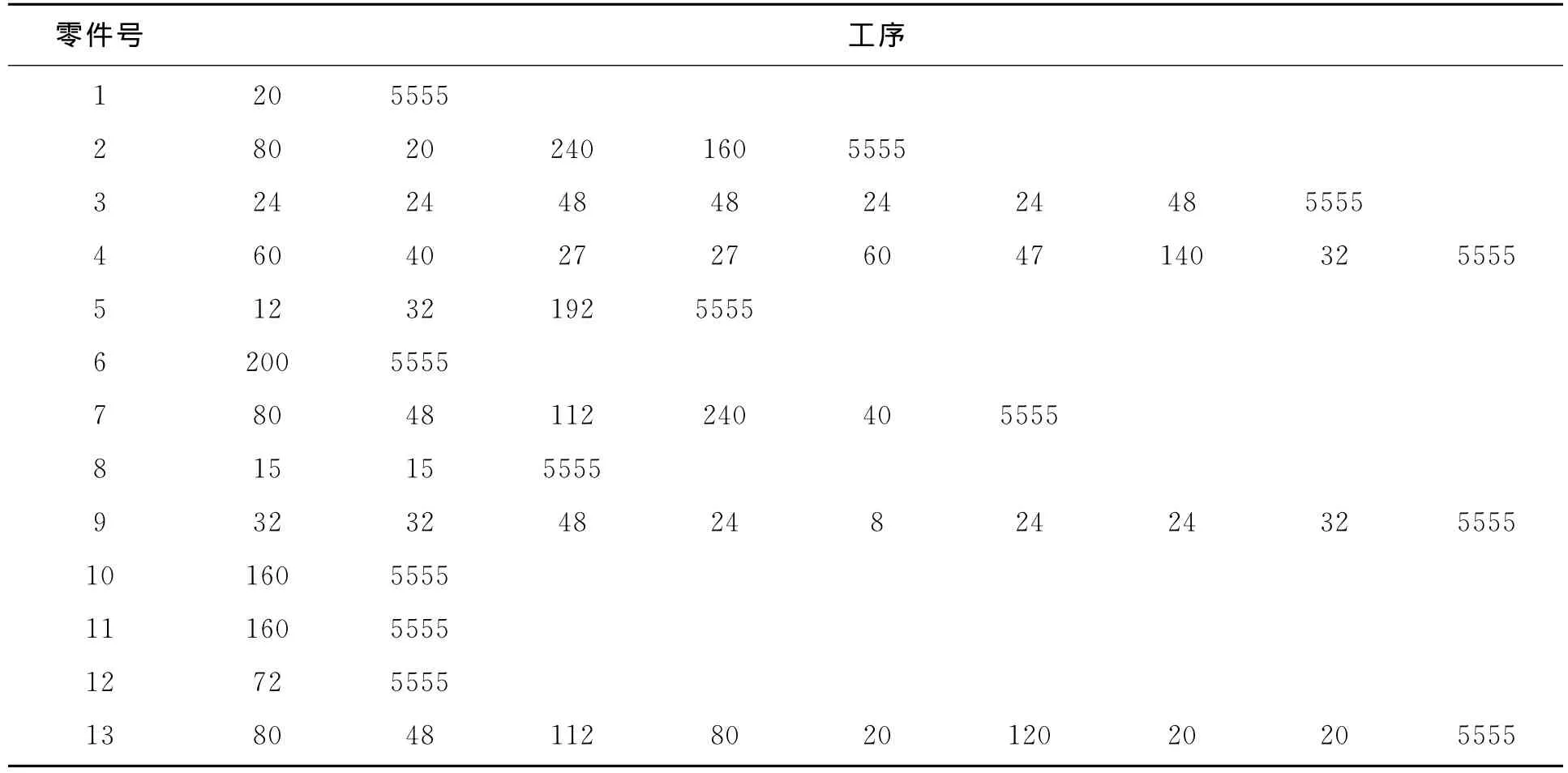
表3 工件的加工时间矩阵

表3表示工件的加工时间矩阵，其初始数据也是存储在txt的文件当中，其中“5555”也是换行标志。

2.2 实验结果

针对问题本身进行了如下处理，对于机器M7，M9，M10，由于均不在本车间加工，且它们都是进行热处理之类的工序，故假设其加工能力很强，对于同时进入外车间的工件可以同时进行加工，且能够保证按时完工。对于工件能在多台机器上加工的情况，根据其可用于加工的机器，从总体上将其化为一个整体中，然后根据全部划分，对这些机器整体进行编号。

2.2.1 标准遗传算法

标准遗传算法是从一组调度解出发，利用各种遗传操作实施大范围的解空间探寻，通过评价函数对每个解进行评估，保留好的种群，并以此来不断寻找最佳的调度解。该方式具有寻找最优解的能力，但该方式本质上是以随机方式进行的，其寻找过程可能是漫无目的和无价值的运算过程，求解质量无法保证。

标准遗传算法的生产调度Gantt图如图1所示。

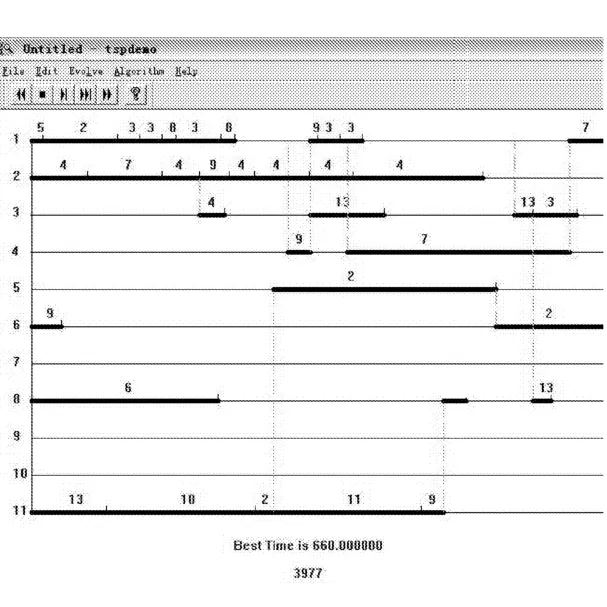
图1 标准遗传算法的生产调度Gantt图

图1是使用标准遗传算法运行3 944代后生成的Gantt图，完成工程的总时间为660h，效果不理想。

2.2.2 混合遗传算法

在解决工件与机器之间一对多的关系上，标准遗传算法是随机确定的，缺乏目的性。文中设计的程序在处理一对多问题上，为每个个体添加了一个机器加工矩阵，所谓机器加工矩阵，是指程序根据个体的工件序列以及机器顺序矩阵和加工时间矩阵来确定工件的各道序的机器加工分配矩阵。针对这一问题，文中巧妙地利用基于机器最短加工时间的方法来生成机器加工矩阵，程序每次访问个体的一个基因（工序），就调用一次排序函数对所有机器按工作时间长短进行升序排列，然后根据工序可调度的机器与排序后的机器进行比较，来确定工件的工序的加工机器，直到完成机器加工矩阵。

混合遗传算法的生产调度Gantt图如图2所示。

图2 混合遗传算法的生产调度Gantt图

图2是文中设计的混合遗传算法在运行60代之后生成的Gantt图结果，完成整个工程的时间为520h，比对图1标准遗传算法660h的结果，混合遗传算法的效果明显优于标准遗传算法，并在取得较好结果的同时其运行代数也明显少于标准遗传算法。

3 结 语

将机器最短加工时间的概念融入算法中的混合遗传算法，全面引导遗传算法的搜索过程，从而避免了单一使用启发式规则给遗传算法带来的早熟现象。当某一工序出现可选择多台机床时，使用机器最短加工时间的启发式方法来选定机床，可实施解的局部优化，大大减少了遗传算法的搜索空间，并以此提高算法的效率与染色体的质量。由此可见，混合遗传算法充分体现了其探索解空间的能力，由此也证明了混合遗传算法充分结合启发式方法与遗传算法的优势，实例考证也说明了混合遗传算法的有效性。

［1］ 王凌.车间调度及其遗传算法［M］.北京：清华大学出版社，2003.

［2］ 张长水，沈刚，阎平凡.解Job-shop调度问题的遗传算法［J］.电子学报，1995（1）：346-348.

［3］ 金芬，孙春华，钟鸣.遗传算法中适应度函数的改进［J］.机械设计与制造，2010（3）：217-219.

［4］ De Jong K A.Genetic algorithm：a 25year perspective，computational intelligence imitating Life［C］／／The Institute of Electrical and Electronics Engineers，Inc.1994.

［5］ Srinivas M，Patnaik K M.Adaptive probabilities of crossover and mutation in genetic algorithms［C］／／IEEE Transactions on Systems，Man and Cybernetics.1994.

［6］ 曾益.一种基于改进遗传算法的车间调度问题研究［J］.机械设计与制造，2011（7）：180-182.

［7］ 王凌.基于遗传算法的Jobshop调度研究进展［J］.控制与决策，2001，16（1）：641-646.

［8］ 沈斌，周莹君，王家海.基于自适应遗传算法的Jobshop调度［J］.计算机应用，2009，29：161-164.

［9］ 孟祥萍，张红，王晖.基于混合遗传算法的泵站优化运行［J］.电气应用，2008，29（1）：30-33.