人工蜂群算法在OFDM系统中的应用

陈 亮

（泰山职业技术学院信息工程系，山东泰安 271000）

0 引 言

正交频分复用技术OFDM在无线通信中应用广泛。OFDM系统的主要缺点是当信号的峰值平均功率比PAPR过高时，可能导致误码率升高［1］。为解决该问题，研究出了大量的能够降低PAPR的算法，如SLM，TR，ACE，PTS等，TR，ACE虽然不会引起信号失真，但是信号传递过程中能量消耗偏大，SLM既不导致信号失真，也不消耗较大的能量，但是应用过程比较复杂［2］。PTS是一个无信号失真、有效降低PAPR的算法，是目前应用最广的降低PAPR的算法［3］。文中提出了一个基于人工蜂群算法的的PTS算法，其搜索量较低，有效地降低了PAPR，克服了传统PTS算法的缺点。

1 系统模型

系统的模拟图如图1所示。

图1 系统模拟图

首先，对用户的输入数据位流进行正交变换，除去信号传递过程中产生的突发差错，正交信号通过数字调制器进行映射后，用PTS算法处理以降低PAPR。为能在系统的接收端取得OFDM的原始信号，需要在PTS阶段向后传递部分边信息。在信号中插入循环前缀的作用是通过高功率放大器放大信号，以除去码间干扰。然后从信道中将信息分离出来，并在信号接收器中除去循环前缀。使用FFT（快速傅里叶变换）和相位旋转，有利于从边信息中取得OFDM的原始信号。再使用数字调制器进行解调信号。最后进行逆正交变换，输出信号。

1.1 OFDM系统的PAPR

定义1 在OFDM系统中，时间上连续的复合信号包定义为：

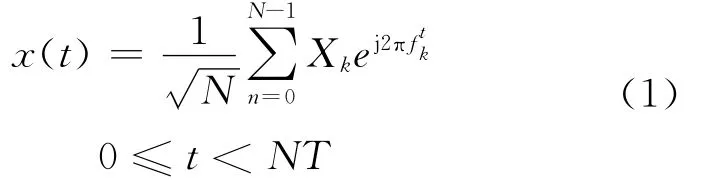
其中，输入数据为X＝［X0，X1，…，XN－1］，N为载波频率。X中的每个通过正交调幅进行映射，并且分配到一个频段fk＝kΔf，0≤k≤N－1，其中，Δf＝1／NT，T是OFDM信号的生存周期。然而，PTSD需要的是时间上离散的信号，因为OFDM信号的一个假设：

其中，L为取样因子，当L＝4时，取OFDM的信号样本，这时，基于时间离散的PAPR与基于时间连续的PAPR几乎相同。采样的OFDM信号为x＝［x0，x1，…，xN－1］，时间上离散的PAPR表示为：

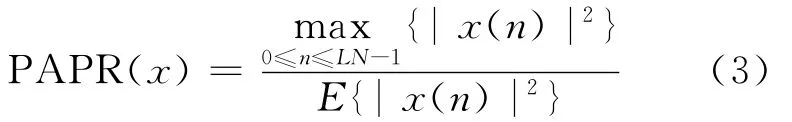
式中：E｛·｝——OFDM信号的期望值。

通常用互补累积密度函数作为PAPR降低的评价标准［4］，一般表示为：

式中：PAPR0——PAPR某个值。

1.2 降低PAPR的PTS算法

PTS的模块图如图2所示。

图2 PTS模块图

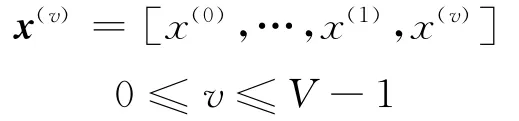
每个子向量按相位因子bv＝ejφ，φ∈［0，2π］变换，最后得到的子向量重新装配，经过PTS处理后的OFDM信号为：

PTS算法的目的是找到优化的相位因子。在优化过程中，第一个子向量的相位因子取值为asb0＝1，若b＝［b1，b2，…，bV－1］，W是相位因子，则用WV－1修正b，得：

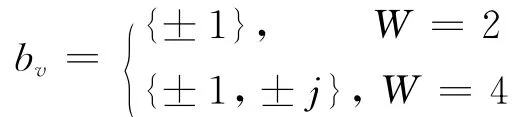
1.3 SSPA和TWTA模型

SSPA和TWTA是非线性振幅调节器，用于OFDM信号的振幅调节［5］。若信号出现变形，采用SSPA和TWTA模型的OFDM系统的误码率有所降低［9］。SSPA的AM／AM和AM／PM的特征值为：

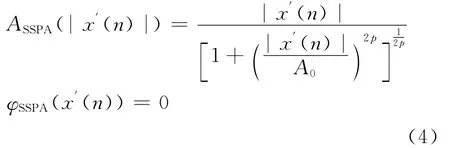
式中：｜x′（n）｜——输入信号的振幅；

A0——输出饱和振幅；

p——平滑控制系数；

ASSPA——输出信号的振幅；

φSSPA——输出相位响应最小值。

由上面定义SSPA的输出信号为：

式中：θ（x′（n））——x′（n）相位。

则TWTA的AM／AM和AM／PM的特征值为：

式中：Ain——输入饱和电压；

ATWTA——输出信号振幅；

φTWTA——最小相应值。

由此定义TWTA的输出信号为：

SSPA和TWTA的工作点由参数IBO决定。

式中：pave，in——信号x′（n）平均功率；

pmax——SSPA和TWTA的峰值功率。

2 基于人工蜂群算法的PTS算法

人工蜂群算法是模拟蜜蜂的觅食行为。在人工蜂群算法中，蜜蜂分为雇用蜂、跟随蜂和侦察蜂，它们的任务是发现最优的食物源，第一个食物源的位置是随机给定的［6］。在降低PAPR的问题中，食物源的位置等同于相位向量bi＝［bi1，bi2，…，bi（V－1）］，i＝1，2，…，SN，其中，SN表示蜜蜂的数量（包含雇用蜂和跟随蜂），雇用蜂在前一个食物源的邻域内查找一个新的食物源。如果新的食物源的花蜜量比前一个大，新的食物源被记为一个可能的最优解。文中定义相位向量（即新的食物源）为：

式中：bk——bi邻域内的一个解；

φi——一个随机数，φi∈［－1，1］。

食物源的食物数量决定解的适应度。解的适应度表示为：

式中：f（bi）——信号的PAPR的值，希望其值最小。

雇用蜂与同一蜂巢中的跟随蜂共享食物源的适应度，跟随蜂能否找到食物源，依赖于这个适应度的值。跟随蜂找到食物源的概率为：

跟随蜂到达一个食物源后，在食物源的邻域内查找一个新的食物源，根据适应度大小决定是否记下这个新的食物源［7］。雇用蜂和跟随蜂完成查找后，食物源的适应度达不到最低要求，则令雇用蜂变为侦察蜂。侦察蜂随机查找新的食物源：

式中：min（bi）——相位向量的下界；

max（bi）——相位向量的上界。

在一个循环中重复执行以上步骤，最多执行MCN次，在一个循环中可能产生SN个解。因此，文中算法中最多产生MCN＊SN个解［8］。

人工蜂群算法的步骤如下：

1）初始化相位向量bi；

2）使用式（9）估算每个向量的适应度；

3）在雇用蜂的位置使用式（8）计算bi邻域内的新的相位向量，并用式（9）计算的适应度；

4）跟随蜂使用式（10）选择食物源；

5）跟随蜂使用式（8）查找新的相位向量，并用式（9）估算每个适应度；

6）如果没有达到最小值的要求，则转4），否则继续；

7）发出一只侦察蜂，用式（11）随机查找一个新的相位向量；

8）记下最好相位向量的解；

9）重复执行5）～8），直到循环次数达到MCN。

3 实 验

设定OFDM系统的载波频率N＝256，采用基于格雷码的正交振幅调制解调器。在SSPA模块中，IBO＝0，3，6dB，p＝0.5，在TWTA中，IBO＝0，3，6，9dB。传输信号的采样因子L＝4。信道采用高斯和瑞利平坦衰落模型。在PTS中，OFDM的信号随机划分到V＝16个子块，当相位因子数W＝2时，相位因子bv∈±1。按搜索条件的数量评价人工蜂群算法的PTS和RS-PTS，每次都重新创建序列b＝［b1，b2，…，b（V－1）］。在RS-PTS中，b的元素随机选定。

3种算法的PAPR性能比较如图3所示。

图3 3种算法的PAPR性能比较

图3显示基于OFDM原始信号的人工蜂群算法PTS和最优PTS的降低PAPR的性能。当I＝MCN×SN时，人工蜂群算法PTS的查找次数接近I＝［64，256，1 024］。MCN×SN的值选定为16×4，64×4，256×4，最小值选定为10。当Pr｛PAPR（x）＞PAPR0｝＝10－3时，OFDM信号的PAPR为11.22dB。人工蜂群算法PTS的PAPR是7.50dB，最优化PTS的PAPR是6.64dB。

文中算法取不同参数时BER如图4所示。

图4 文中算法取不同参数时BER

图4显示使用瑞利平坦衰落信道的人工蜂群算法PTS的误码率的性能。当误码率BER＝10－5时，线性放大器的误码率性能值SNR＝12dB，这个值比参数IBO＝6dB，p＝2的SSPA低0.9dB。当p＝2时，SNR的值分别为16.3dB，14.2dB，12.9dB，此时的IBO为0，3，6dB。当参数IBO＝3dB，p＝0.5和IBO＝3dB，p＝2时，SNR分别为16dB和12dB，BER＝10－4。

4 结 语

提出了一个新的基于人工蜂群算法的PTS算法，有效降低了OFDM系统的PTS算法的计算复杂度。实验结果表明，人工蜂群的PTS与RS-PTS在降低PAPR的性能上几乎是相同的，但是在相同条件下，人工蜂群PTS的计算次数少了4次。

［1］ 蓝良生.基于正交频分复用技术的低压电力线载波宽带通信的研究与实现［J］.科技信息，2012（8）：136-137.

［2］ Yue J，Li Z，Liu L，et al.Content-based image retrieval using color and texture used features［J］. Mathematical and Computer Modelling，2011，54（3／4）：1121-1127.

［3］ 赵黎，柯熙政，孙林丽.降低FSO-OFDM系统峰值平均功率比研究［J］.红外与激光工程，2011（9）：1749-1753.

［4］ 胡滢，杨桂芹.降低OFDM系统中PAPR的技术分析［J］.信息通信，2012（1）：73-74.

［5］ Karaboga D，Akay B.A comparative study of artificial bee colony algorithm［J］.Applied Mathematics and Computation，2009，214：108-132.

［6］ 梁聪.一种带功率检测和自适应偏置的CDMA功率放大器［J］.固体电子学研究与进展，2011（1）：81-84.

［7］ 陈亮.基于混合蛙跳算法的背包问题求解算法［J］.河南城建学院学报，2011，20（3）：41-44.

［8］ Roy G G，Chakraborty P，Das S.New method for modelling and simulation of the dynamic behaviour of the wheel-rail contact［J］.International Journal of Bio-Inspired Computation，2010（2）：303.

［9］ 张海涛，郭大波.多媒体通信技术的现状与待解决问题［J］.长春工业大学学报：自然科学版，2011，32（5）：449-452.