一类双层多目标规划问题的若干等价形式

魏彦吉， 陆 晶， 刘庆怀

（1.长春工业大学基础科学学院，吉林长春 130012；2.吉林农业大学发展学院基础部，吉林长春 130600）

0 引 言

双层规划问题（Bilevel Programming Problem，BLPP）是一类特殊的平衡约束优化问题，在工程学和经济学方面应用广泛，如经济规划、农业信贷分配、网络设计、机器学习、交通运输规划、模式识别等［1－5］。所以，近几年越来越受到人们的重视。许多学者对其进行了深入研究，提出了许多解决双层规划的算法。J F Bard和J T Moore［6］等研究提出了求解该问题的分支定界算法，Aiyoshi和Shimizu［7］等提出了罚函数法解决双层规划问题，但算法收敛速度比较慢，2004年，徐庆［8］等提出用同伦算法来求解双层规划问题，徐俊彦［9］等提出解线性互补问题的组合同伦方法，为双层规划算法的研究注入了新的活力。文中在平凡的条件下，给出了上层是多目标，下层是单目标的双层多目标规划问题（简称BMOP）的若干等价形式。

1 基本概念与记号

考虑BMOP问题：

其中，（x，y）∈Rn＋m，f：Rn＋m→Rp，F：Rn＋m→R分别是上层和下层目标函数，g＝（g1，g2，…，gs）T：Rn→Rs，G＝（G1，G2，…，Gl）T：Rn＋m→Rl分别是上层和下层约束条件。

文中使用记号如下：

S（x）——问题（1）下层的解集。

文中假设如下：

1）存在开集A⊆Rn，对任意x∈A，有D（x）≠φ；

2）存在有界开集Rm⊆B，使得对任意x∈A，有D（x）⊆B；

4）对任意x∈Ωx且y∈S（x），｛▽yGi（x，y），i∈（y）｝是线性独立的；

5）对 任 意 的 （x，y）∈Ω，其 梯 度｛▽gi（x，y），i∈Ig（x，y）｝是线性独立的。

对于BMOP问题（1），设f，F，g，G都是充分光滑的，F，G是凸的。

首先，考虑BMOP问题（1）的下层问题：

如果对于给定的点x∈Rn，则｛y∈Rm：G（x，y）＜0｝是非空的，下层优化问题的KKT系统可写为：

那么问题（1）可等价转化为如下关于变量（x，y，u）的优化问题：

下面将问题（2）等价转换为如下问题：

其中，z∈Rl，它的引入只是为了后面证明的方便，并不是必须的。最小算子min是按z和u的分量取最小，即

若引入函数h0：Rn＋m＋l＋l→Rm＋l＋l如下：

则上面的问题可紧凑地写为：

从而由假设条件易知，问题（4）等价于问题（2），即等价于问题（1），亦即（x＊，y＊）是问题（1）的一个全局（局部）解的充要条件，是存在一个向量（z＊，u＊）使得（x＊，y＊，z＊，u＊）为问题（4）的一个全局（局部）解。

为了处理互补型约束，文中引进由Kanzow和Jiang［1］提出的NCP函数φμ：R2→R：

式中：μ——扰动参数，μ＞0。

其中

那么，当μ≠0时，可定义最优化问题：

问题（6）是问题（4）关于参数μ的一个光滑扰动问题，尽管问题（4）一般情形下非光滑，但当μ≠0时，问题（6）则是一个光滑最优化问题，且当μ＝0时，问题（6）与问题（4）等价。

记

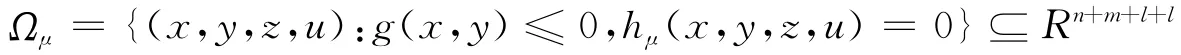
表示问题（6）的可行集，记

表示问题（6）的严格可行集，从而Ωμ的边界可表示为：

将μ看做独立变量，函数hμ则依赖于5个变量（x，y，z，u，μ），从而得到如下定理。

定理1 对任意的μ和问题（6）的可行点（x，y，z，u）∈Ωμ，关于变量（y，z，u）的所有hμ的广义Jacobian矩阵是非奇异的。

证明：我们引进的函数φμ（z，u）恰好与文献［1］中使用的函数互为相反，从而很容易证明这种改变从根本上并不影响在文献中关于函数φμ（z，u）非奇异性质的证明。因此，当μ≠0时，本定理的结果是文献［10］中定理3.5的一个直接推论；而当μ＝0时，本定理的结果是文献［1］中引理2的一个直接推论。

由文献［1］可类似证明hμ有如下性质：

引理1 任意的μ，函数hμ（x，y，z，u）是局部Lipschitz连续和正则的。

引理2 设（μ＊，x＊，y＊，z＊，u＊）是hμ（x，y，z，u）＝0的一个解，则存在（μ＊，x＊）的一个邻域Ωμ，x和一个连续函数（y，z，u）：Ωμ，x→Rm＋l＋l，使得对任意（μ，x）∈Ωμ，x，有

引理3 给定x＊∈Ωx，则对任意μ，存在唯一点（x＊，yμ（x＊），zμ（x），uμ（x＊））∈Ωμ使得hμ（）＝0，且θ＊μ作为μ的函数是连续的。

由上述引理可得如下定理。

定理2 对任意μ知，Ωμ为非空紧集，扰动问题（6）有Pareto最优解。

由此，求解BMOP问题（1）可转化为解优化问题（6）。

即

2 结 语

通过以上讨论，求解BMOP问题（1）就可通过同伦方法转化为问题（2），再利用最小算子min将问题转化为问题（3），引入函数h0：Rn＋m＋l＋l→Rm＋l＋l将问题转化为（4），最后利用NCP函数转化为解非线性优化问题（6）和问题（7），并证明了解之间的关系。从而发现寻找更好的解决问题（7）的方法尤为关键，接下来将完善问题（7）的求解并给出数值例子。

［1］ 林锉云，董加礼.多目标最优化方法与理论［M］.长春：吉林科技出版社，1992.

［2］ 刘庆怀，林正华.求解多目标规划最小弱有效解的同伦内点方法［J］.应用数学学报，2000（2）：188-195.

［3］ 李佳民，刘庆怀.解一类双层规划问题的组合同伦方法［J］.吉林大学学报：理学版，2007，45（2）：213-215.

［4］ Hobbs B F，Nelson S K.A nonlinear bilevel model for amalysis of electric utility demand-side planning issues［J］.Ann.Oper.Res.，1992，34：255.

［5］ GarciaC B，Zangwill W I.Pathuays to solutions，fixed points and equilibria［M］.Prentice-Hall：New Tersey，1981.

［6］ Bard J F，Moore J T.A branch and bound algo-rithrn for the bilevel programming problem［J］.SIAM Journal on Science and Statistical Computing，1990，11（2）：281-292.

［7］ Aiyoshi E，Shimizn K.A solution method for the static constrained stackelberg problem wia penalty method［J］.IEEE Trans.，Automat，Contr.，1992，34：1111-1114.

［8］ Zhu Daoli，Xu Qing，Lin Zhenghua.A homotopy method for solving bilevel programming problem［J］.Nonlinear Analysis，2004，57：917-928.

［9］ 徐俊彦，苗壮，谭佳伟，等.解线性互补问题的组合同伦方法［J］.长春工业大学学报：自然科学版，2010，31（3）：269-274.

［10］ Kanzow C，Jiang H.A cortinuation method for（strongly）monotone variational inequalities［J］. Math.，Prog.，1998，81：103-125.