GCOA算法

王晓丽++贾东明

摘要： 根据种群中个体的竞争与淘汰机制提出了一种群体竞争优化算法（GCOA）。首先对算法的构造思想进行了详细的描述，然后用本算法求解具有多个极值点函数的最大值，从而分析算法的可行性。最后，使用本算法对物流车辆路径的优化问题进行了仿真研究，得出了算法的先进性。

Abstract： The group competition optimization algorithm is proposed according to the mechanism of competition and elimination of individuals in the population. At first， it describes the construction of the algorithm， solves the maximum value of the function that have multiple extreme points by this algorithm. Then， draw the conclusion that the algorithm is feasible. Finally， the optimization of the logistics vehicle routing problem is simulated by using this algorithm， and the advanced nature of the algorithm is obtained.

关键词： 淘汰机制；协作机制；编码方式；路径优化

Key words： elimination mechanism；cooperation mechanism；coding mode；routing optimization

中图分类号：TP18 文献标识码：A 文章编号：1006-4311（2017）22-0170-02

1 算法的提出

作者通过麦特·里德雷所著的《美德的起源》一书中对群体中个体互助合作从而保证种群顺利传承的一段论证，捕捉到进化的实质，即协作与淘汰，同时根据上述机制构造了一种种群进化算法，而算法的目的是希望种群能够得到优化。编码方式：为了将现实的问题与算法进行匹配或映射，我们需要对求解空间进行编码操作。淘汰机制：在一个种群里随机产生的若干个体，必须要经历淘汰。协作机制：个体经历淘汰之后，种群中个体的数量必然会减少，可以在这个时候引入一些新的个体，以保证种群大小不变。

2 实际问题的解决

该算法依靠群体的进化特性而进行优化，最终可以求取最优解。为了验证算法的可行性，对函数f（x）=x+10sin（5x）+7cos（4x），自变量取值在[0，10]范围内的最大值进行求解。函数在自变量规定的取值范围内，有8个极大值。可以通过这样的函数来分析本算法是否会陷入局部最优。

2.1 编码 用20位的二进制码代表函数的自变量，20位的二进制码转化为十进制码的话，范围在[0，220 -1]。因此需要将本范围的数据与自变量范围[0，10]内的数据对应起来。

2.2 淘汰 将本代中所有的个体求取适应度值，然后依据适应度值的大小将个体进行升序排列，将适应度值最小的N个个体清零。

2.3 协作 随机选取最优个体的10位连续二进制数字转化为新进个体的同一位置，对于每个新个体所得到的位置均不相同。其余未选中的部位随机产生二进制数字。

2.4 返回至第二步进行循环计算，直到规定的代数为止。上述问题求解过程中总共规定了100代。

2.5 分析 在上述的1、2、3步中，第3步是最为重要的。因为新产生的个体继承了最优个体的部分特性，并且随机产生了其余位置的数据。如若继承的部分恰巧是具有优良特性数段的话，那其余部分数据改变相当于在最大值附近寻优，保证了寻优过程的持续进行。如若继承的部分并不是最优的数段，则此个体保证了数据在全局范围内随机找最大值，那么数据陷入极值点被吸附的可能性就大为降低。因此第3步保证了全局最优的寻找以及最优值的精确化。

2.6 问题的解决 文章随机产生一个具有50个个体的群体，每次淘汰30个个体，同时新产生30个个体进行最优化学习。每次学习时都是随机产生一个点位，并将最优个体同一点位之后连续的10位数字学习到自身，然后进行仿真。仿真进行了20次，每次均能找到最优点。程序运行中一次进化稳定所经历代數较少的结果，但并不能保证每次运行都在如此短的代数之内将问题解决。即使如此，所有20次仿真，在100代之内均找到了问题的最优解。因此得出了本算法可用于最优化问题求解的可行性结论。

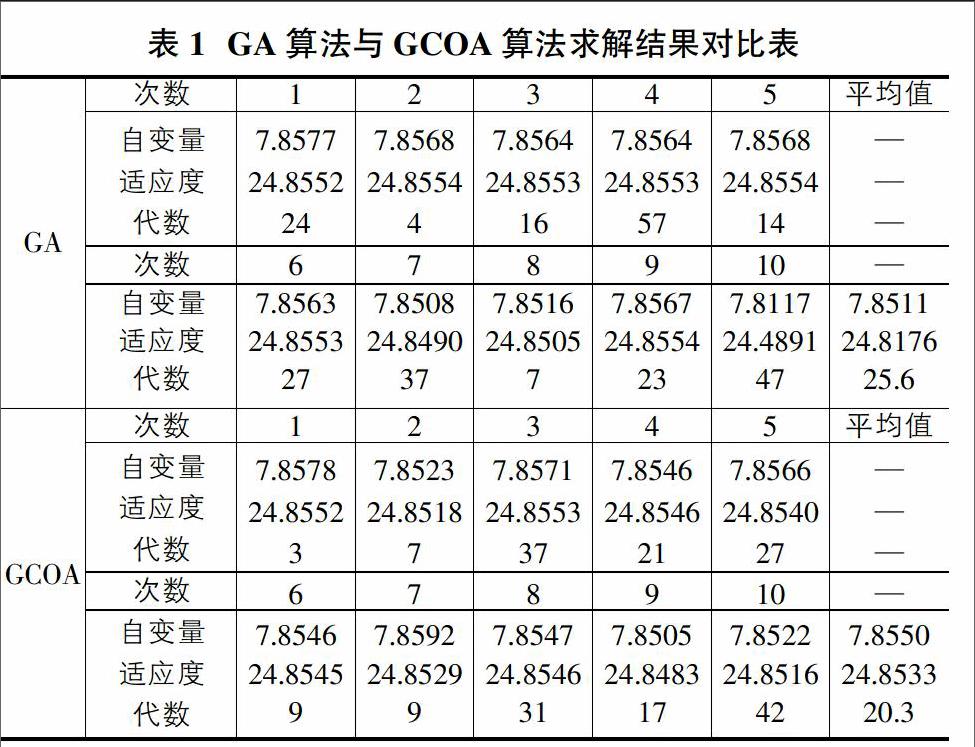
2.7 算法的进一步探讨 作者对本算法与遗传算法分别进行编程，进行本问题的最优解求取，然后将结论进行对比，求解结果对比见表1。

由求解结果对比表可见：使用GA算法求取的最优值是24.8176，使用GCOA算法求取的最优值是24.8533。使用GA算法求取最优值时平均需要经历26代，而GCOA算法需要经历20代。由此可见，对于本例所使用的函数来说，GCOA算法无论从最优值还是从迭代代数来说，都是优于GA算法的，并且值得一提的是，GCOA算法比GA算法的设计思路更为简洁，用MATLAB程序进行实现时，GCOA编制了47行，而GA编制了74行。

3 GCOA算法在物流车辆路径优化中的应用

3.1 VRP问题的数学描述 已知一个配货中心（用0表示）需将货物配送至n（1，2，3…n）个客户点，每个客户点的需求量为qi（i=1，2，3…n），客户点i到j的距离是Cij（i，j=1，2，3…n），每辆车的载货能力均为Q，设T为实际使用到的车辆数，第K辆车经过的客户点总数用nk表示，集合Rk={rki|0？燮i？燮nk}表示第k辆车经过的客户点。

假设从配货中心派出的车辆是统一的，即所有车辆的载货能力是相同的。则问题须同时满足下面列出的所有条件：

①任何一辆车都可从配货中心出发，经过多个客户点而返回配货中心，但所装载的货物不能超出车辆的载货能力；

②每个客户点都只能被一辆车供货；

③所有客户点的需求必须都能够被满足；

④求解所有车辆运送路径的最小值。

3.2 问题的解决

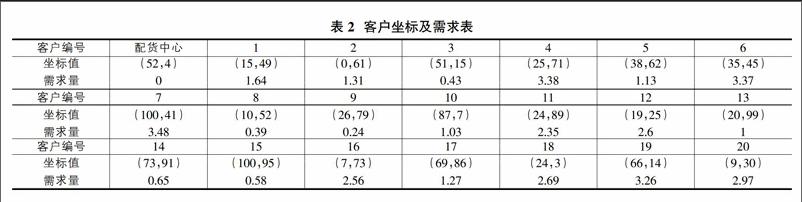
文章主要解决具有1个配货中心，20个客户点的VRP问题。文中采用了被国内多篇文献所引用的数据进行求解，以便于进行结果的对比。各客户点的需求量如表2所示，车辆的容量为8吨。

对于两坐标点之间的距离，使用直线距离来进行计算，并应用GCOA算法来对此实际问题进行求解，解决思路如下：①编码。本问题求解使用实数编码来进行。比如15-14-17-4-5-3-6-18-9-11-13-16-2-8-1-20-12-19-7-10代表了车辆走过的路径，但是此链中不是一辆车可以解决所有的问题，所以我们依次对客户的需求量进行求和，如果某段的和小于8，但再加一个点后和就大于8的话，此段即为一辆车运输。

②淘汰。在第一代时，随机产生了50个个体作为一个种群。每次淘汰其中的30个个体。所使用的目标函数是总路径最短，优化的目的是使目标函数最小。我们可以将目标函数的倒数作为适应度函数，依然以求取适应度值最高为目标。每次淘汰的30个个体都是适应度最低的30个个体。

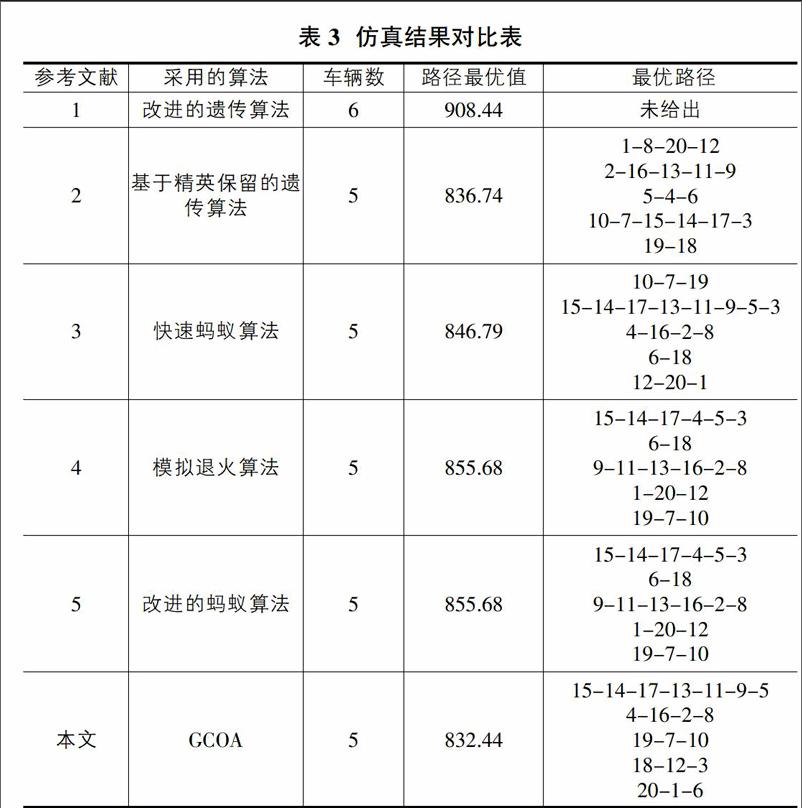
③协作。协作的过程依然是新产生的30个个体向最优个体学习的过程，选择的目标段依然是连续10位数据的组合，并且点位随机产生。

④仿真结果。通过表3的对比结果可以看出，文章所提出的GCOA算法得出的结论是最优的。而且经过多次运行之后，GCOA算法所得出的结果范围大致在850-890之间，具有很好的稳定性。

4 结论

文章提出了GCOA算法并使用Matlab软件对多极值点函数及VRP问题进行了优化求解，最终得出了算法可行性及优越性的结论。此算法刚被提出，并未经过大量的实践验证，也许有些潜在的问题是作者未考虑到的。因此作者下一步的工作目标将是应用此算法求解更多的优化问题，以求发现并改良算法中存在的问题。

参考文献：

[1]程林辉.基于改进的遗传算法的车辆路径问题研究[D].中南民族大学硕士论文，2008：32-33.

[2]安立军.遗传算法在物流配送车辆优化调度中的研究与应用[D].上海海事大学硕士论文，2007：19-33.

[3]辛焦丽，高丽.基于遗传算法的蜂窝网络接入信道动态分配方案的设计[J].现代电子技术，2016，39（15）：5-7.

[4]王凤云，冉文学，张巧霞.蚁群算法在卷烟配送路径优化中的应用研究[J].物流技术，2011（05）：69-72.

[5]鐘惟钰.遗传算法在物流配送运输车辆路径优化中的应用和改进[J].物流技术，2014，33（5）：323-325.