基于ANSYS Workbench的ZC1型蜗杆副瞬态动力学分析*
马玉娟,吉卫喜,宋丽娟,靳小马
(江南大学 机械工程学院,江苏 无锡 214122)
0 引言
ZC1型蜗杆副是一种常被用于自动扶梯上的传动装置,蜗轮蜗杆啮合时的齿面接触线是空间曲线,变化规律较为复杂,沿接触线上各点的曲率半径和蜗轮轮齿形状在齿宽方向上也是不断变化的[1]。对这种新型蜗杆副进行瞬态动力学分析,以此分析蜗杆副啮合过程中动力学特性,为蜗杆副后续的优化设计提供依据。
对于蜗杆副的静力学问题前人做了很多的研究,但是对于蜗杆副的动力学问题研究比较少。Feng等[2]基于柔性多体模型研究了瞬态过程中高功率密度齿轮传动的动态问题,数值和理论结果证实了瞬态对动态力和变形的显著影响。 此外,齿轮传动过渡状态的合理时间可以避免大的冲击力,减少齿轮系统的振动和噪声。李福海等[3]建立了系统的瞬态动力学模型,经过分析获得凸轮机构一个工作循环过程中,凸轮盘等效应力、应变随时间的变化为凸轮机构再设计优化及加工制造提供一种新思路。蒋灿琼等[4]对减速器齿轮系统进行瞬态动力学分析,获取了齿轮系统在不同频率下的振动情况。在此基础上对齿轮进行修形,以达到使齿轮传递更加平稳,减少齿轮噪声,改善NVH性能的目的。项昌乐等[5]提出了一种履带车辆动力系统动力学模型,模型中考虑了齿侧间隙、非线性摩擦因数可用于预测系统的高频动力学行为,以期有助于系统的优化设计。
针对ZC1型蜗杆副。首先,基于空间啮合理论,建立ZC1型蜗杆副啮合方程,借助MATLAB和Soildworks软件接口建立三维实体模型;然后通过有限元软件对其进行瞬态动力学分析;最后对ZC1型蜗杆副与盘形锥面包络圆柱蜗杆副的动力学性能进行对比分析。研究结论为ZC1型蜗杆副后续的优化设计和试验数据校验提供依据。
1 ZC1型蜗杆副的啮合方程
1.1 ZC1型蜗杆副的坐标系设置
建立如图1所示的 ZC1型蜗杆副坐标系,S1(O1,i1,j1,k1),Sσ(Oσ,iσ,jσ,kσ),Sw(Ow,iw,jw,kw),Sp(Op,ip,jp,kp)。其中,坐标系S1(O1,i1,j1,k1)是空间动坐标系,它与蜗杆相固联,k1轴与蜗杆轴线重合;坐标系Sσ(Oσ,iσ,jσ,kσ)也是空间动坐标系,它与圆环面盘形砂轮相联接,且砂轮轴线正好与kσ轴相重合;坐标系Sw(Ow,iw,jw,kw)是空间定坐标系,kw轴与k1轴重合;坐标系Sp(Op,ip,jp,kp)是为了表达蜗杆与蜗轮之间运动关系而建立的空间辅助定坐标系,kp轴与kσ轴相重合,ip轴与iw轴相重合。图中点Q为蜗杆与蜗轮啮合过程中的任意一个接触点。已知ZC1型蜗杆副属于空间交错轴传动,轴交角为90°,故k1轴与kσ轴之间的夹角也为90°。蜗杆、蜗轮的转角分别为φ1,φ2,a为蜗杆副的中心距。
1.2 ZC1型蜗杆副啮合方程
图2所示砂轮的轴截面示意图中,G为砂轮圆弧齿廓上任意一点,其参数为θ;砂轮圆弧齿廓母线m-m的转角参数为β;d为砂轮齿廓圆弧中心Oσ′到砂轮轴线(即kσ轴)的距离;c为圆环面盘形砂轮齿廓圆弧中心Oσ′与iσ轴之间的距离;则砂轮工作表面方程为:
(1)
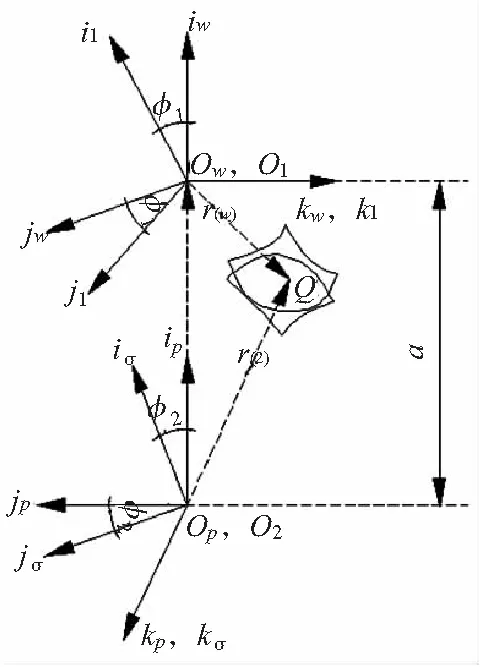
图1 蜗轮与蜗杆啮合的坐标系
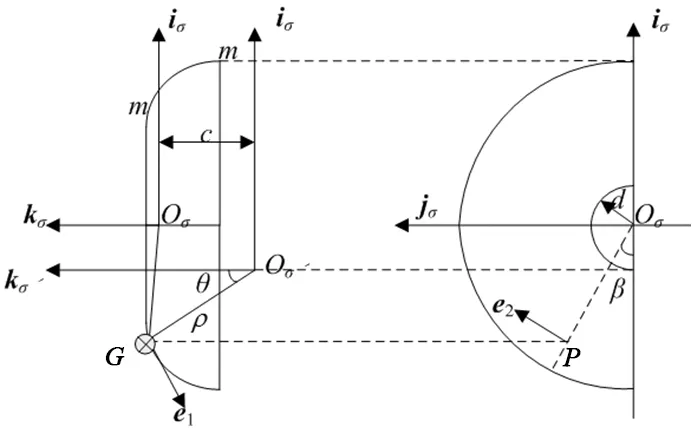
图2 砂轮轴截面
基于ZC1型蜗杆副坐标系的设置情况,根据空间啮合理论[6],推导啮合方程。蜗杆分度圆上的法截面齿形角为α,蜗杆的导程角为γ,蜗杆绕着蜗杆轴线以角速度ω1旋转,转过的角度为δ。蜗杆副的啮合方程为:
(2)
2 ZC1型蜗杆副动力学建模
2.1 三维实体建模
借助MATLAB通过蜗杆啮合方程拟合ZC1型蜗杆螺旋线,借助Soildworks的三维制图功能对ZC1型蜗杆进行三维建模,运用虚拟加工的方法使蜗杆对蜗轮毛坯进行布尔减运算以完成蜗轮的实体建模,最后利用虚拟装配得到蜗杆副实体模型。蜗杆副模型参数如表1所示。

表1 ZC1型蜗杆副主要设计参数
2.2 有限元模型的建立
2.2.1材料属性定义
20CrMnTi是性能良好的渗碳钢,经渗碳淬火后具有硬而耐磨的表面,常用于蜗杆等传动件。蜗轮材料则选择铸造锡青铜CuSn12。故在ANSYS中定义蜗杆副材料属性如表2。
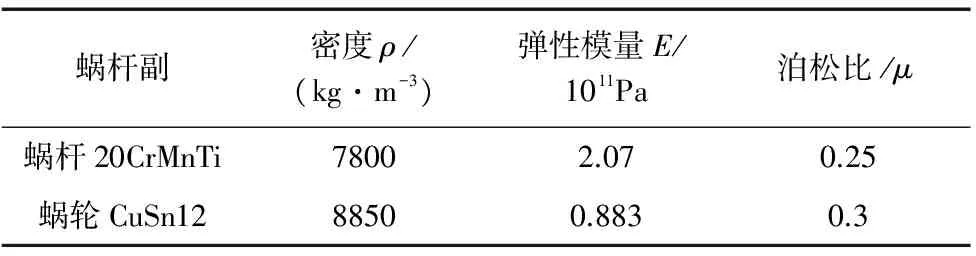
表2 蜗杆副材料
2.2.2网格划分
蜗杆副体单元选用Solid185,每个节点有三个沿着xyz方向平移的自由度,单元支持塑性、超弹性、蠕变、应力钢化、大变形和大应变能力[7]。充分考虑蜗杆副接触面特性,定义接触单元为TARGE170和CONTA174[8]。蜗杆的网格单元尺寸为0.15mm,蜗轮的网格单元尺寸为0.1mm,蜗杆和蜗轮接触区域的5个轮齿的网格单元尺寸为0.05mm。蜗杆副网格划分图如图3所示。

图3 ZC1型蜗杆副有限元模型
3 瞬态动力学分析
借助有限元分析软件ANSYS WORKBENCH 对ZC1型蜗杆副进行瞬态动力学分析。
3.1 瞬态动力学方程
瞬态动力学分析是时域分析,是分析结构在随时间任意变化的载荷作用下,动力响应过程的技术[9]。瞬态动力学的通用方程[10]:

(3)
3.2 ZC1型蜗杆副瞬态分析
3.2.1施加载荷及约束
蜗轮与蜗杆之间的接触类型为frictional,摩擦系数设为0.2;转动副定义为revolute连接。蜗杆为主动件,蜗轮为从动件。已知蜗杆的输入转速为n= 1000r/min,且
RotationalVelocity=2πn/60
(4)
则Rotational Velocity ≈ 105 rad /s。
蜗杆副输出力矩计算公式为:
M/T=i
(5)
式中,M为输出力矩,N·m;T为主动轮输入扭矩,N·m;i为蜗杆副的传动比。
设置蜗杆(主动件)输入扭矩为 268.832 N·m,则M=1774.29 N·m。
3.2.2结果后处理
按照表2和式(4)、式(5)提供的的参数,利用瞬态动力学分析方法,得到ZC1型蜗杆副的等效应力云图、等效应变云图、总变形云图,如图4~图7所示。
图4为蜗杆副整体等效应力图,最大等效应力发生在蜗杆上,其值为814.992 MPa。
图5为蜗杆局部等效应力图,从图上可看到,最大等效应力发生在蜗杆螺旋线靠近中心附近,并且向四周由大到小分布。蜗杆材料为20CrMnTi,屈服极限在 800~835MPa 之间,分析结果验证了实际运行中蜗杆磨损较严重的现象。
图6为蜗轮局部等效应力图,蜗轮的最大等效应力发生在齿顶位置,最大等效应力为134.39MPa,小于材料屈服极限应力170 MPa。

图4 蜗杆副等效应力图 图5 蜗杆局部等效应力图

图6 蜗轮局部等效应力图 图7 蜗杆副总变形量图
图7可知,ZC1型蜗杆副的最大变形量为2.333×10-3m,出现在蜗杆的边缘,且距离蜗杆轴的中心越远变形量越大。所以为了避免因蜗杆的轮齿变形导致蜗杆副过早失效,在设计阶段应合理考虑蜗杆的径向尺寸。
4 两种蜗杆有限元分析结果对比分析
为研究ZC1型蜗杆副的承载能力和变形等方面的动态特性,基于ANSYS瞬态动力学分析方法,对两种有较好发展前途的ZC1型和ZK1型蜗杆副的动力学特性进行对比分析。
4.1 ZC1型蜗杆副与ZK1型蜗杆副分析结果
ZK1型蜗杆副的蜗杆是用盘形锥面砂轮包络而成的圆柱蜗杆,其齿面是圆锥面族的包络面。蜗轮则是以加工得到的蜗杆经过开槽、铲背处理制成蜗
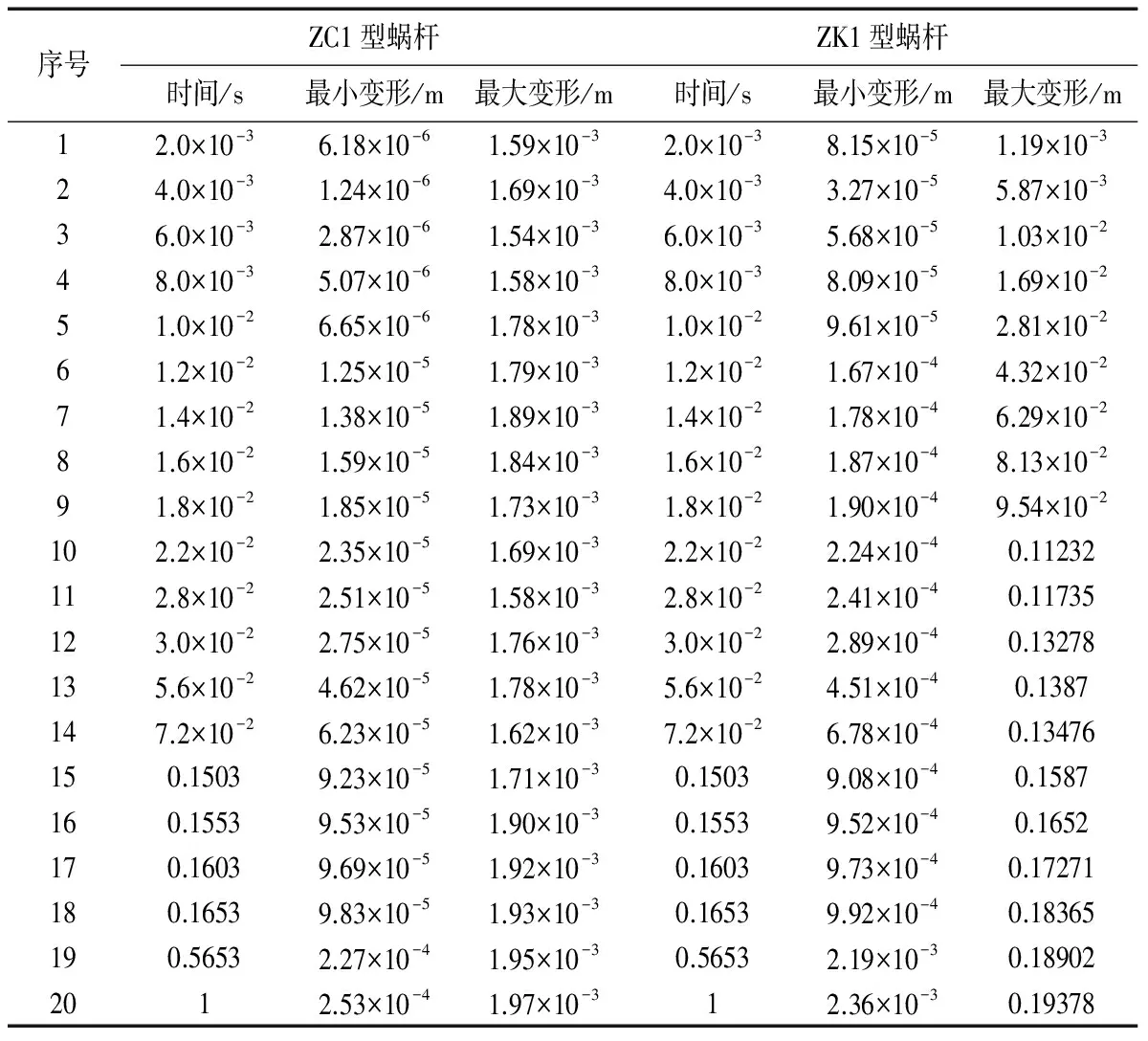
表4 ZC1型和ZK1型蜗杆变形结果对比
轮滚刀后加工而成。ZK1型蜗杆与ZC1型蜗杆传动相似,但ZK1型蜗杆副的共轭齿面是凸凸啮合的,而ZC1型蜗杆副是凹凸齿廓相啮合的,这是两种蜗杆最大的区别。
基于空间啮合理论,建立ZK1型蜗杆副啮合方程,借助MATLAB和Soildworks软件接口建立ZK1型蜗杆副实体模型。建模过程限于篇幅,此处不再详述。图8所示为ZK1型蜗杆的实体剖切模型。
图8 ZK1型蜗杆实体模型
假设输入转矩为268.83N·m,运用ANSYS对蜗杆副进行静力学分析,则可获得相应的等效应力及接触应力。
表3为ZC1型蜗杆副和ZK1型蜗杆副瞬态动力学分析结果之间的对比。
表3可以看出,ZC1型蜗杆副的蜗杆等效应 力 为 ZK1型蜗杆副蜗杆的84.5%,ZC1型蜗杆副的蜗轮等效应力为ZK1型蜗杆副蜗轮等效应力的61.1%,ZC1型蜗杆副的接触应力为ZK1型蜗杆副的76.44% 。对比结果表明,在采用几乎相同的参数、输入扭矩情况下,ZC1型蜗杆副比ZK1型蜗杆副具有较高的承载能力。因此,ZC1型蜗杆副比ZK1型蜗杆副更适合重载的环境。
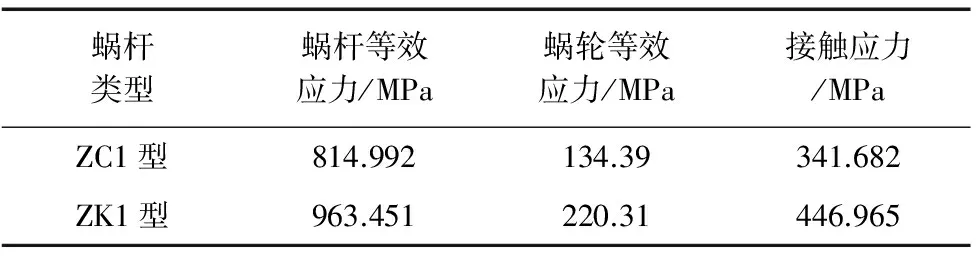
表3 ZC1型蜗杆副与ZK1型蜗杆副分析结果
4.2 ZC1型蜗杆副与ZK1型蜗杆副分析结果比较
假设ZK1型蜗杆副输入额定转矩274.636 N·m,其他参数设置与ZC1型蜗杆副相同,对比结果如表4。ZC1型蜗杆副和ZK1型蜗杆副在瞬态动力学分析中随时间变化的变形量结果如表4、图9、图10。
由表4可知,在ZC1型蜗杆副瞬态分析过程中,当t=0~1s时,蜗杆副的变形量始终≤0.0023m。ZK1型蜗杆副瞬态分析过程中,当t=0.5653s时,最小变形量为0.0019m。
图9为ZC1型蜗杆副瞬态运动过程中总变形的时域曲线。
图10为ZK1型蜗杆副瞬态运动过程中总变形的时域曲线。
由图9、图10可知,同一时间内,设置相同的参数、输入扭矩时,ZK1型蜗杆副比ZC1型蜗杆副随时间变化的变形量变化大。可见,在瞬态分析过程中,ZC1型蜗杆副的抗变形能力较强,故ZC1型蜗杆副更适合重载、复杂的工作环境。
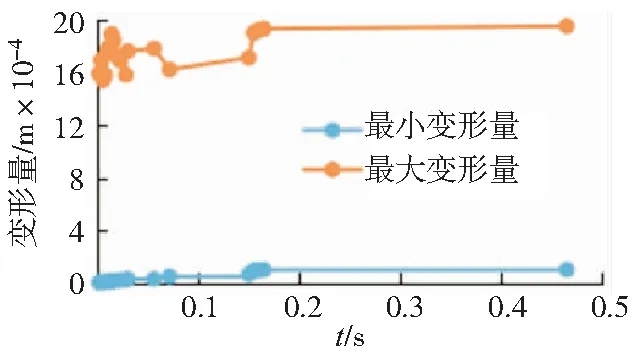
图9 ZC1型蜗杆副变形量-时间曲线图

图10 ZK1型蜗杆副变形量-时间曲线图
5 结论
建立了ZC1型蜗杆副瞬态动力学模型。基于非线性接触有限元法对蜗杆副进行瞬态动力学分析。对ZC1型蜗杆副、ZK1型蜗杆副进行对比分析。
(1)ZC1型蜗杆副瞬态啮合过程中,蜗杆承受的最大等效应力为814.992 MPa,蜗轮承受的最大等效应力为134.39MPa,总体最大变形量为2.3339×10-3m。满足材料屈服极限及强度要求,为蜗杆副后续的优化设计提供依据。
(2)通过对两种有发展前景的蜗杆副瞬态分析实例可知,设置相同的参数、输入扭矩时,ZC1型蜗杆副
比ZK1型蜗杆副的承载能力更大,ZC1型蜗杆副比ZK1型蜗杆副的抗变形能力更强,所以ZC1型蜗杆副更适用于自动扶梯这种重载的工作环境。研究结论为ZC1型蜗杆副后续的优化设计和试验数据校验提供依据。
[参考文献]
[1] 王树人.圆弧圆柱蜗杆传动[M]. 天津:天津大学出版社,1991.
[2] Feng Haisheng,Wang Liqin Zheng, Dezhi Zhao, et al. Transient dynamic analysis of high power density gear transmission[J]. Proceedings of the institution of Mechanical Engineers,2014,228(12):1443-1451.
[3] 李福海,张宏文,李勇,等. 摘锭式采棉机凸轮机构的瞬态动力学分析[J]. 机械设计与制造,2013(4):128-130.
[4] 蒋灿琼. 某减速器NVH性能的分析与优化[D].长沙:湖南大学,2016.
[5] 项昌乐,何韡,刘辉,等. 履带车辆传动系统换挡工况瞬态动力学分析[J]. 农业机械学报,2016,47(4):288-293.
[6] 谭昕.平面二次包络环面蜗杆副数字化造型理论及仿真研究[D].武汉:武汉理工大学,2003.
[7] 杨泽青.基于复杂系统理论的高速数控加工装备动静态特性监控技术研究[D]. 天津:河北工业大学,2010.
[8] 张志民,樊喜刚,周志刚,等. 基于ANSYS的摆线齿锥齿轮有限元模态分析与研究[J]. 新技术新工艺,2015(1):100-102.
[9] 杨福芹,丁中敏,王培超,等. 地震载荷下家用救生舱的瞬态动力学分析[J]. 机电工程,2015,32(3):370-372,383.
[10] 王凯,姚进,邓星桥,等.无侧隙端面啮合蜗杆副瞬态动力学分析[J]. 工程科学与技术,2017(1):86-94.
(编辑李秀敏)

