预紧力对滚柱直线导轨副振动特性的影响研究*
陈 蓉,欧 屹,冯虎田
(南京理工大学 机械工程学院,南京 210094)
0 引言
近年来,滚动直线导轨因其传动效率高、定位精度好等优点被广泛应用于数控机床、半导体制造设备及检验设备的高精度定位、导向系统中。为了防止机械设备破坏,提高加工精度,通常要求设备的工作频率避开各阶固有频率,所以对装备进行动力学分析就显得尤为重要,而对导轨副进行动力学分析的关键在于对其结合面的动态特性研究。目前,对滚动直线导轨的静力学特性研究比较多,而对其动态特性的研究相对较少。在目前的研究中,很多学者选择用弹簧来代替滚动体模拟导轨和滑块的接触[1-2],Hiroyuki Ohta用阻尼弹簧代替滚珠,建立了滚珠直线导轨的动力学模型,利用有限元分析软件建模求解,并通过实验说明了模型的不同模态对系统动力学性能的影响,但是由于所用的弹簧单元数量较多,有限元分析时对计算机的要求较高。毛宽民[3]在系统分析国内外有关滚动直线导轨动力学特性研究成果的基础上,提出了一种直线滚动导轨副结合部动力学模型,并通过实验验证了该模型的合理性。在仿真计算方面,也有多位学者提出了用ADAMS建立滚柱直线导轨副的仿真模型[4-5],并验证了其正确性。
另外,在实际应用中,线性导轨通过增大滚动体的过盈量来增大预紧力,进而增加线性导轨的结构刚度和承载能力。根据已有的研究[6],由于结合面接触刚度的变化,预加载的线性导轨将具有不同的振动特性,这将直接影响线性导轨整体结构的刚度和动态特性。
本文通过ADAMS仿真分析和锤击实验相结合的方法,研究预紧力对滚柱直线导轨副固有频率的影响,这对研究机床振动和振动控制以及准确进行机床动态设计和优化设计具有重大意义[7]。
1 滚柱直线导轨副的振动模型
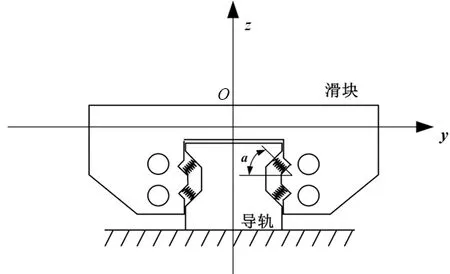
图1 导轨副简化模型
为了缩短软件分析时间,使计算简便,需要将滚柱直线导轨副模型进行简化。基于文献[8-9]的研究,类似的将滚柱直线导轨副简化成如图1所示,因为阻尼在模态计算中对导轨副的固有频率影响很小,所以本文不考虑阻尼的影响,使简化后的模型仅仅包含滑块和导轨两部分,并用弹簧代替滚柱连接滑块和导轨。线性导轨的典型振型有俯仰、侧翻、偏航以及上下运动,如图2所示。参考文献[5],本文使用8个弹簧单元代替滚柱直接连接滑块和导轨,模拟直线导轨结合部,建立了一个多刚体的振动模型。其中弹簧处在四滚道内滑块长度方向1/4和3/4处。
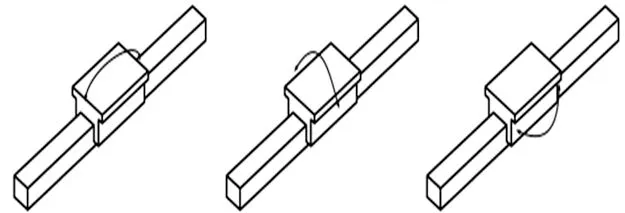
(a)俯仰 (b)侧翻 (c)偏航图2 线性导轨的典型振型图
2 结合面处的接触刚度计算
简化过程是对分析对象进行适当的简化,以便于软件进行分析计算,但是也要确保原始分析对象的主要结构力学性能不发生改变,所以简化模型和原始模型在滚道结合面处的接触刚度应该相同,本文以Palmgren的经验公式为理论依据,计算每个滚柱的接触刚度,从而得到模拟弹簧单元的等效刚度[10-11]。
滚柱直线导轨副可以通过滚柱直径的过盈量(Δ)给予导轨副预紧力来提高刚度,预紧力P与滚柱所受法向力Q之间的关系为:
P=iZQcosα
(1)
其中,i为沟槽数,i=2;Z为单列有效承载滚柱个数;α为接触角。
根据Palmgren的经验公式,滚柱直线导轨副接触部分的弹性变形量为:
(2)
其中,δ为导轨与滚柱的法向弹性趋近量;μ为材料的泊松比;E为材料的弹性模量;l为滚柱的有效长度。
由于滚柱与导轨接触面和滑块接触面的弹性变形量相同,所以滑块和导轨之间的总变形量应为2δ,则有:
(3)
文中采用的研究对象为广东高新凯特精密机械股份有限公司的LGR45型滚柱直线导轨副,该直线导轨的滚柱与导轨、滚柱与滑块为线接触,在导轨副受到高载荷作用时仅仅形成微小的弹性变形,使得导轨副的刚性得到很大的提高。导轨副采用DB45度组合,能承受上下左右四向等载荷。该导轨副的相关参数如表1所示。

表1 LGR45型滚柱直线导轨副的相关参数
考虑到滚柱分别与滑块和导轨有相对趋近量,所以每根模拟弹簧的刚度为:
(4)
其中,k=Q/δ为单个滚柱的接触刚度。
3 ADAMS仿真求解
本文采用了三种不同预紧等级的滚柱直线导轨副,预紧力分别为0.025C、0.05C、0.1C,其中C为滚动直线导轨副额定动载荷;根据表1所示的各项参数,可以计算出对应的模拟弹簧刚度分别为:959N/μm、1016N/μm、1084N/μm。然后将简化的滚柱直线导轨副导入到ADAMS仿真软件进行分析求解,ADAMS动力学仿真模型如图3所示,仿真得到系统的各阶固有频率及振型,结果如表2所示。
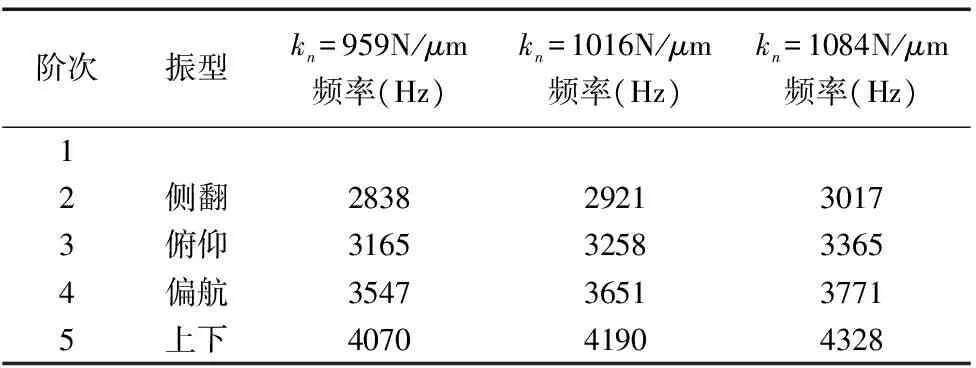
表2 三种不同预紧下的导轨副的固有频率
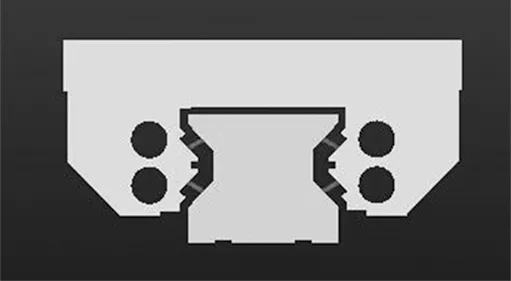
图3 ADAMS动力学仿真模型
从表2中我们可以看出,随着预紧力的增大(即模拟弹簧刚度的增大),各阶固有频率也相应的增大,说明了导轨副的固有频率受预紧力的影响。
4 导轨副模态实验
模态实验主要是为了研究滚动直线导轨的动态特性,测得导轨系统的动态特性参数,主要为导轨的固有频率,以便于考察理论模型和有限元模型的准确性。本次实验釆用锤击法测试导轨的固有频率,实验原理如图4所示,所用的主要仪器设备有击振锤(型号:PCB PIEZOTRONICS 086C03)、振动加速度传感器(型号:PCB PIEZOTRONICS 356A02)、数采系统(型号:PROSIG P8020)。
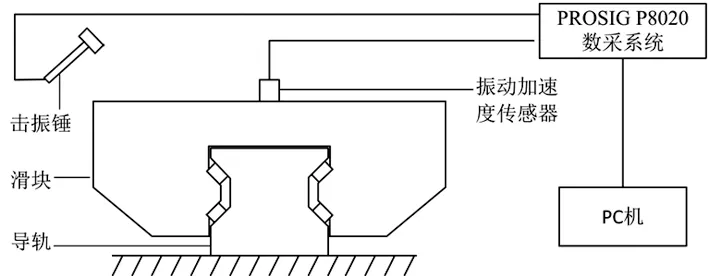
图4 模态试验原理图
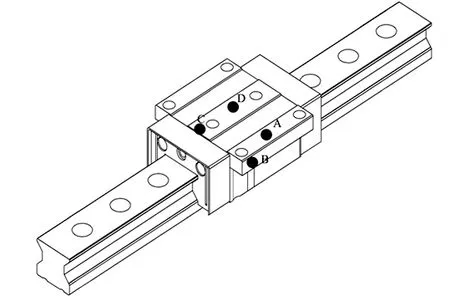
图5 振动加速度传感器布置图
由第一节我们知道,线性导轨的典型振型有俯仰、侧翻、偏航以及上下运动,将振动加速度传感器按图5所示分别布置在滑块的A、B、C、D四点处可以测得导轨系统的侧翻、偏航、俯仰和上下运动的固有频率。实验过程如下:将实验装置设备按图6顺序连接好,传感器釆用胶粘方式固定,用击振锤在测量方向上连续敲击滑块3下,通过滑块上的三轴加速度传感器检测导轨系统的振动信号,并将振动信号通过信号线传输给数采系统,振动信号通过PROSIG P8020数采系统进行滤波和信号放大,最终通过笔记本上DATS Analysis软件采集获得导轨系统的固有频率。

图6 锤击试验装置图
试验得到的不同预紧下滚柱直线导轨副的各阶固有频率结果如图7~图9所示。
从图7~图9中,我们可以看出当预紧力增大时,滚柱直线导轨副的各阶固有频率都有相应的增大,这是因为当滚柱直线导轨副的预紧力增大时,其刚性得到提高,而导轨副的固有频率与刚度呈正相关[12],所以导轨副的固有频率会因为预紧力的增大而增大。为了对比仿真结果与实验结果的误差,绘制表3。从表3中可以看出,在不同预紧下仿真和实验得到的滚柱直线导轨副的各阶固有频率值基本吻合,误差基本都在10%以内,验证了结果的可靠性。为了更清晰地看出预紧力不同对滚柱直线导轨副各阶固有频率的影响,绘制图10。
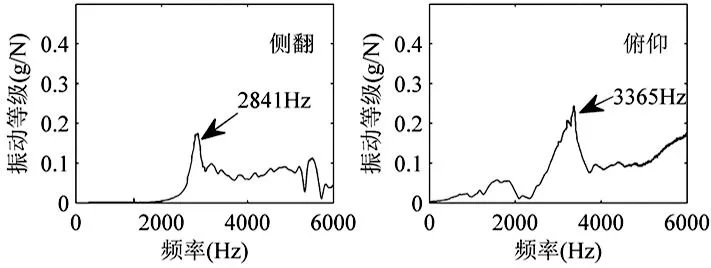
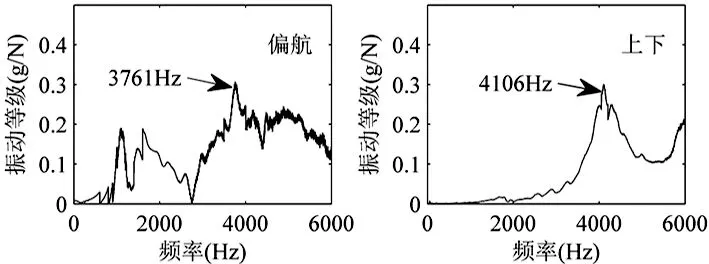
图7 预紧为0.025C时导轨副的各阶固有频率
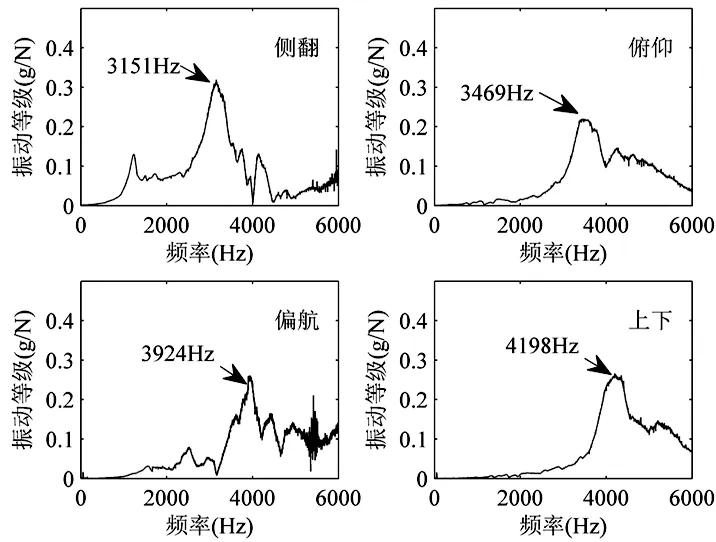
图8 预紧为0.05C时导轨副的各阶固有频率
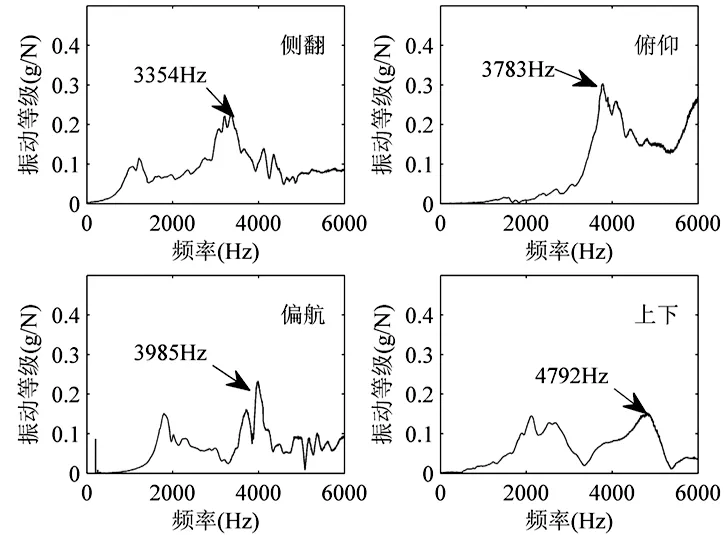
图9 预紧为0.1C时导轨副的各阶固有频率
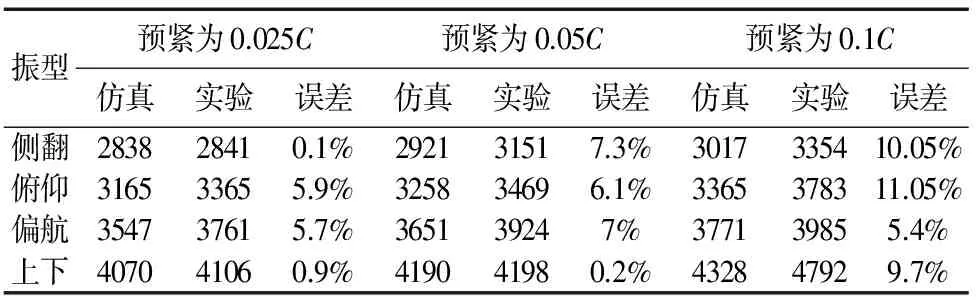
表3 不同预紧下导轨副固有频率的仿真结果与实验结果对比
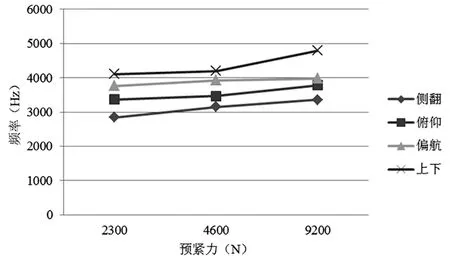
图10 预紧力对各阶固有频率的影响
从图10中我们可以更清晰直观地看出,预紧力对滚柱直线导轨副的各阶固有频率都有影响,且随着预紧力的增大,导轨副的各阶固有频率都表现出非线性的增长趋势,这是因为预紧力通过影响导轨副的接触刚度进而对整个导轨固有频率产生影响。预紧力的增大导致了滚柱直线导轨副结合部刚度的提高,进而使得导轨副固有频率随之出现增长的趋势,这说明滚柱直线导轨副固有频率与预紧力之间也呈正相关。
5 结论
本文基于ADAMS仿真分析和锤击实验相结合的方法,探究得滚柱直线导轨副的各阶固有频率均随预紧力的增加而呈非线性增加,两者之间的关系为正相关。实验结果可以有效的应用于机床的振动研究中,对使用不同预紧导轨的机床有效地避开共振以提高加工质量或防止机床损坏有重要作用。研究结果为用户选取滚柱直线导轨副类型提供了参考。
[参考文献]
[1] Ohta H, Hayashi E. Vibration of linear guideway type recirculating linear ball bearings[J]. Journal of Tribology, 1999, 121(4):847-861.
[2] Wu S S, Chang J C, Hung J P. The effect of contact interface on dynamic characteristics of composite structures[J]. Mathematics & Computers in Simulation, 2007, 74(6):454-467.
[3] 毛宽民,邢满禧,李斌,等. 滚动直线导轨副可动结合部动力学建模[J]. 华中科技大学学报(自然科学版),2016,36(7):85-88.
[4] 荣伯松,宋现春,姜洪奎,等. 基于ADAMS的滚柱直线导轨副的动态仿真[J]. 组合机床与自动化加工技术,2011(10):31-35.
[5] 成建平,杨家军,程远雄,等. 滚柱直线导轨结合面的振动分析[J]. 机电工程,2013,30(3):296-299.
[6] Chang J C, Wu S S J, Hung J P. Characterization of the dynamic behavior of a linear guideway mechanism[J]. Structural Engineering & Mechanics, 2007, 25(1):1-20.
[7] 周传宏,孙健利. 滚动直线导轨副动态特性的试验研究[J]. 机械设计与制造工程,2001,30(2):14-15.
[8] Hung J P. Load effect on the vibration characteristics of a stage with rolling guides[J]. Journal of Mechanical Science and Technology, 2009, 23(1):89-99.
[9] 宁昰超. 滚动直线导轨动态特性研究[D]. 大连:大连理工大学,2016.
[10] 刘曙光,孙健利. 滚柱直线导轨副的力学性能分析[D]. 武汉:华中科技大学,2011.
[11] 李慎奎. 直线滚动导轨结合面动态特性的研究[D]. 沈阳:东北大学,2008.
[12] 马雅丽,宁昰超,钱峰. 滚动直线导轨固有特性分析[J]. 华中科技大学学报(自然科学版),2016,44(9):59-64.
(编辑李秀敏)

