基于响应面模型和集成方法的数控机床整机优化*

张在房，张佳翔

(上海大学 机电工程与自动化学院，上海　200072)

0　引言

机床整机零部件众多、装配关系复杂，对于数控机床这类复杂的整机结构，在优化设计过程中不能建立精确的数学模型，优化方法仍局限于传统的设计方法，其本质是工程师根据设计经验，反复修改结构尺寸，从有限的可行方案组里面选取仿真效果最理想的设计方案。这种设计方法不是建立在数学模型的基础上，难以保证方案的最优性，而且优化效率显然无法满足现代数控机床设计的需要。

近年来，基于响应面模型的研究和优化设计方法的研究已经成为国内外学界重点研究的课题之一。

1　响应面法与集成方法

1.1　哈莫雷斯试验设计方法

哈莫雷斯[7](Hammersley)试验设计方法属于蒙特卡洛法的一种，是在哈莫雷斯点的基础上应用随机采样的方法。该方法是一种随机生成均匀样本的试验设计和抽样方法，也是空间填充试验研究方法，抽取的样本数据点分布比较均匀，可使样本均匀地布满整个设计空间，而且可以保证所有因素在每个水平上能均匀地应用。因此，哈莫雷斯试验方法能够用少量的试验点获取尽可能多的信息，是一种高效、均衡的试验设计方法。

1.2　响应面模型的拟合

响应面法[8](Response surface methodology，RSM)是以数理统计为基础，通过构造一个明确的函数表达式，得到响应函数和约束函数的响应面模型。为了解决机床整机优化问题无法通过解析式准确表达的困难，选取设计变量的二阶多项式构造响应面函数。对于n个设计变量的情况，变量X与响应值Y(X)之间的响应面函数形式为：

式中，X=(x1,x2,…，xn),Xi(i=1,…，n)为设计变量；y为输出变量；αo为常数项，αi为一次项系数，αii为二次项系数，αij为未知数，规定α的个数为(n+1)(n+2)/2，α可通过最小二乘回归法确定。

2　基于多目标粒子群算法和协同优化算法相结合的优化策略

在制定优化策略时，要求具有较强的全局搜索能力和鲁棒性，防止局部收敛，能够收敛到全局最优解集；同时，由于优化模型的复杂性，容易造成计算模式繁杂、学科分析的响应时间过长等问题，此时要求优化策略具有较强的局部搜索性，获取局部最优解。粒子群算法的全局搜索性和鲁棒性较强、搜索效率高，但对于复杂的工程问题往往适应性较差，很难得到满意的优化结果。而协同优化算法对实际工程应用具有较好的适应性，但多维不规则的设计空间容易导致计算量较大，求解时间太长。因此结合这两种优化方法的思想，充分发挥各单一优化算法的优点。利用粒子群的全局搜索优势，先采用粒子群算法对整个设计空间进行全局寻优，多次迭代得到全局近似最优解集后，将包含近似最优解集的设计空间作为二次优化的设计空间，缩小寻优空间范围，利用协同优化算法在新的设计空间进行局部优化，直至收敛于最优解。这种二次优化逐次逼近的思想对于高度复杂的多学科优化问题具有较为突出的表现。具体的优化策略流程图如图1所示。

图1　优化流程

由于多目标粒子群初始优化的目的是进行全局搜索，获取Pareto最优解集，其对初始种群要求比较高，因此采用Hammersley[11]抽样技术来获取粒子群算法的初始种群。Hammersley 抽样技术是一种准随机数抽样技术，它能够为样本点提供最佳位置以便于更好的均匀分布。具体的优化流程如图2所示。

图2　基于多目标粒子群初次优化的流程

在初次优化的基础上，对全局设计空间进行缩小，缩小的空间是包含最优解及其附近的局部空间，接着利用协同优化算法在局部空间内对问题进行二次优化，获取最优设计方案，验证优化结果是否满足约束条件，各项性能是否得到提升。机床整机协同优化与多目标粒子群优化共用近似模型，不同的是设计空间。协同优化的流程如图3所示。

图3　基于协同优化算法二次优化的流程

3　数控机床整机优化

图4为某型号数控机床CAD简化模型，数控机床主要由床身、立柱、主轴箱、滑台和工作台五大核心部件组成。

图4　数控机床整机三维简化模型

3.1　数控机床优化模型的建立

3.1.1数控机床静动态特性

通过有限元分析对数控机床整机进行静动态特性的分析，得到最大形变量和前3阶固有频率。如图5所示。

(a) 静载下变形云图　　(b) 1阶模态振型云图

(c) 2阶模态振型云图　　(d) 3阶模态振型云图图5　仿真结果图

由图可知机床整机的最大变形为71.396μm，主要发生在主轴箱的顶部，因此应对主轴箱的结构进行进一步优化。立柱的前3阶固有频率分别为41.58Hz、54.26Hz、113.42Hz。由于该型号机床的最高设计转速为5000rpm，机床的激振频率一般位于前几阶模态的固有频率中，故选取前3阶固有频率来表示动态性能。

表1为仿真结果与模态试验结果的对比，从结果来看，仿真结果与试验结果的误差在允许的范围内，因此仿真结果可信度高。

表1　有限元分析与模态试验结果对比

3.1.2设计变量的确定

对数控机床整机进行静态分析和动态分析后，发现整机个别部件的局部存在薄弱环节，需要对这些部件进行尺寸调整以优化整机的性能。选取整机的9个主要尺寸作为设计变量，如表2。

表2　设计变量

3.2　响应面模型的建立

本文基于哈莫雷斯试验设计方法抽取60组样本数据，然后利用数值模拟计算出各组样本数据的响应值，如表3所示。

基于设计变量与响应值的结果，图6为以质量、最大形变量、1阶固有频率、2阶固有频率和3阶固有频率为目标函数做的响应面近似模型。

本文采用R2(决定系数)来评价响应面的预测能力，如图7所示，由图中可以看出，5个目标参数质量、最大形变量、1阶模态频率、2阶模态频率和3阶模态频率的决定系数分别为0.99997、0.99643、0.99861、0.98618和0.9494。由标准化图可以看出，预测值和观测值也非常吻合。因此，响应面模型的总体精度符合要求，可以作为后续优化设计的计算模型。

表3　设计变量与响应值

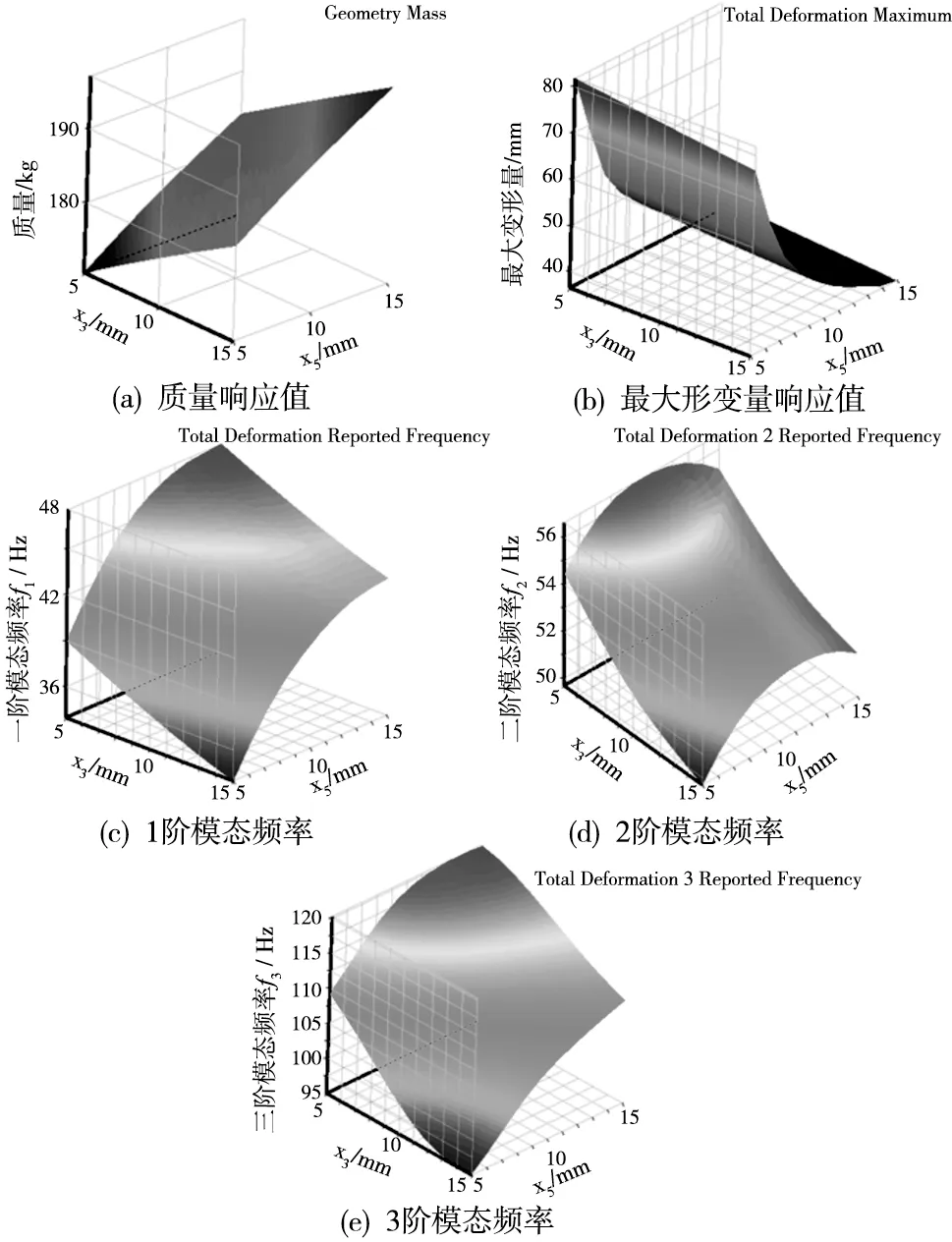
图6　响应面近似模型图

图7　近似模型精度

基于试验设计数据的灵敏度分析方法，根据收集的响应数据，如图8做出了设计变量对质量、最大变形量、前3阶模态频率5个响应的灵敏度图，图中只标注了灵敏度较大的设计变量。由图中可知设计变量对响应值影响比较显著，尤其对最大形变量呈较明显的负影响，说明立柱壁厚对整机的刚度起关键作用，而对质量、1阶固有频率、2阶固有频率和3阶固有频率呈正影响。设计变量主轴箱壁厚主要影响前3阶模态频率。从总体看，设计变量和对整机的性能影响程度比较明显。

图8　变量对响应值灵敏度

3.3　优化模型与求解结果

数控机床整机重量利用数值模拟计算得出，优化的目的是希望机床减重。整机静态性能用刚度来衡量，刚度利用某工况载荷下的最大形变量来表示，最大形变量越小表示整机静态性能越优；根据分析，利用前3阶模态的固有频率来衡量整机的动态性能，一般情况下，希望优化后的前3阶固有频率不低于初始设计方案。本文采用多目标粒子群算法和协同优化算法相结合的优化策略进行整机优化。初次优化将整机优化问题转化为多目标多约束问题进行全局优化，以数控机床重量最小、刚度最优(形变量最小)、1阶固有频率最大为优化目标，2阶固有频率低于初始设计方案，3阶固有频率低于初始设计方案为约束条件，优化的数学模型如下：

minF1(X)=M(X)
F2(X)=c(X)
F3(X)=-f1(X)
s.t.f2(X)≥f20
f3(X)≥f30
X=[x1,x2,…，xh]T

图9　Pareto最优解集

图9为采用多目标粒子群算法进行全局寻优得到的Pareto最优解集，绿色区域为最优解。由图中可以看出，优化过程中呈现集中化的趋势，其趋势表明：一阶固有频率的增加必将导致整机质量的增加和最大形变量的增加，即优化目标之间相互矛盾，因此有必要对最优解的区域再进行局部优化。最优解中的设计变量主要集中在某块局部区域，一般情况，对满足要求的最优解进行设计空间的缩小。

图10为基于协同优化算法的机床整机优化系统框图，优化系统分为系统级优化和4个并行的学科级优化两部分。系统级优化目标为整机重量最优，约束条件为全局变量一致性差异最小。4个相互平行的子学科的优化目标都是局部变量一致性差异最小，子学科1的约束条件为整机最大形变量不大于初始形变量，子学科2的约束条件为1阶固有频率大于等于初始1阶固有频率，子学科3的约束条件为2阶固有频率大于等于初始2阶固有频率，子学科4的约束条件为3阶固有频率大于等于初始3阶固有频率。系统级优化采用修正可行方向算法(MMFD)，4个并行的学科级优化采用非线性二次规划算法(NLPQL)。基于缩小的设计空间进行二次优化迭代。数学模型：

系统级优化数学模型：

子学科1、2、3、4优化数学模型：

表4为优化前后设计变量取值的比较，本文对优化结果进行取整。表5为二次优化后的设计方案对比，从表中可以得出，采用响应面模型和集成方法的优化方法对数控机床整机进行优化后，各项性能都得到了良好的提升，结果理想。

图10　协同优化系统框图

表4　设计变量优化结果

表5　优化结果性能比较

为了验证优化结果的可信度，利用优化前后的有限元模型进行静力仿真，如图11，由图可得优化后的最大形变量为45.405μm，与优化结果非常接近，说明本文提出的方法能够获得正确的优化结果。

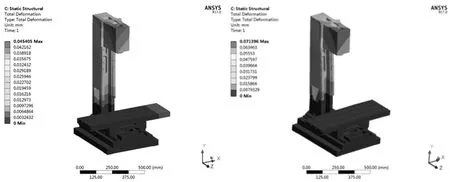
(a)优化前　　　　 (b)优化后图11　整机静态性能优化结果对比

4　结论

本文以某型号数控机床的整机优化为应用对象，综合运用参数化建模、参数化分析、模态试验试验设计、灵敏度分析、响应面近似模型、粒子群算法与协同优化算法相结合的优化策略，提出了一种基于响应面模型的集成优化设计方法。通过整机静动态分析和模态试验，寻找影响机床静动态性能的薄弱零部件。首先建立数控机床整机的参数化模型，针对零部件薄弱环节确定设计变量。然后采用哈莫雷斯试验设计法获取设计空间样本点，利用参数化有限元分析计算求得响应值。基于样本数据建立响应面近似模型。基于近似模型利用粒子群算法进行全局初次优化，在此基础上采用协同优化算法进行二次局部优化，完成优化设计。求解得到的设计方案满足设计要求，有效实现了某型号数控机床的整机优化，具有较高的计算效率和优化结果。本文提出的集成优化设计方法也适用于其他类似复杂结构系统的机床整机的优化问题。

[参考文献]

[1] 吕辉, 于德介, 谢展,等. 基于响应面法的汽车盘式制动器稳定性优化设计[J]. 机械工程学报, 2013, 49(9):55-60.

[2] 姜衡, 管贻生, 邱志成,等. 基于响应面法的立式加工中心动静态多目标优化[J]. 机械工程学报, 2011, 47(11):125-133.

[3] 于海莲, 王永泉, 陈花玲,等. 响应面模型与多目标遗传算法相结合的机床立柱参数优化[J]. 西安交通大学学报, 2012, 46(11):80-85.

[4] Ceruti A, Voloshin V, Marzocca P. Heuristic Algorithms Applied to Multidisciplinary Design Optimization of Unconventional Airship Configuration[J]. Journal of Aircraft, 2014, 51(6):1758-1772.

[5] 苏瑞意, 桂良进, 吴章斌,等. 大客车车身骨架多学科协同优化设计[J]. 机械工程学报, 2010, 46(18):128-133.

[6] 杨丽丽, 陈昌亚, 王德禹. 基于多目标协同优化算法的卫星结构优化设计[J]. 上海交通大学学报, 2014, 48(10):1446-1450.

[7] 史朝军. 基于多学科设计优化的车门结构轻量化研究[D]. 武汉:武汉科技大学, 2014.

[9] Kennedy J, Eberhart R. Particle swarm optimization[C]// IEEE International Conference on Neural Networks, IEEE, 1995:1942-1948.

[10] Kroo I, Manning V. Collaborative optimization - Status and directions[J]. 2006, 26(92):93-103.

[11] 彭艳华. 立式加工中心多目标优化设计[D].广州:华南理工大学, 2011.

(编辑李秀敏)