循环式行星滚柱丝杠副的自由度与运动学分析

侯红玲，李 巧，王艳茹，赵永强,2

（1.陕西理工大学 机械工程学院，汉中 723001；2.陕西省工业自动化重点实验室，汉中 723001）

0 引言

行星滚柱丝杠副作为一种将旋转运动转换为直线运动的新型高精度传动部件，目前运用高速传动、螺距大、高精度等场合，而循环式行星滚柱丝杠副更适用于空间小、螺距小的场合。在行星滚柱丝杠副理论研究方面，Velinsky等建立了SPRS运动学分析模型[1]；岳琳琳等基于有限元仿真研究了行星滚柱丝杠动态特性[5]；靳谦忠等基于行星滚柱丝杠运动简图分析了传动原理及运动关系[6]；祝明路等在建立标准式行星滚柱丝杠空间机构简图的基础上分析了标准式行星滚柱丝杠的自由度[7]；韦振兴等人依据行星齿轮传动原理，对行星滚柱丝杠副的相关设计变量进行参数优化分析[8]；徐强等人建立PWG型丝杠副的传动分析模型计算了差动式丝杠副的导程，试验测量了导程误差，验证了传动模型的正确性[9]；韩敏等建立了丝杠和滚柱之间的相对滑动速度的数学模型，分析研究行星滚柱丝杠副的滑动特性[10]；马尚君等采用显式动力学算法，对行星滚柱丝杠副运转时的动态特性进行分析[11]。

上述文献的研究对象均为标准式和差动式行星滚柱丝杠副，而未曾涉及循环式行星滚柱丝杠副，关于循环式行星滚柱丝杠副设计的相关报道仅限在国外极少数产品样本中。与标准式行星滚柱丝杠副相比，循环式行星滚柱丝杠副采用无螺旋升角的环槽状滚柱，取消了滚柱与螺母之间的齿轮副，增加了实现连续运动的复位凸轮，由此增加了运动的复杂性和容易出现运动不连续的缺陷。

本文以循环式行星滚柱丝杠副为研究对象，基于约束螺旋和机构学理论，建立循环式行星滚柱丝杠副的空间机构运动模型，分析计算循环式行星滚柱丝杠副的机构自由度和运动参数，分析各构件的运动关系，研究相关参数对实际导程的影响，基于ADAMS运动仿真软件，验证循环式行星滚柱丝杠副的工作原理合理性。

1 循环式行星滚柱丝杠副的结构组成和工作原理

循环式行星滚柱丝杠副的结构如图1所示[12]，由丝杠、保持架、复位凸轮、螺母、滚柱等构件组成，与标准式行星滚柱丝杠副相比，保持架替代了内齿圈，滚柱结构形式发展为无螺旋升角的环槽状滚柱，保持架使多个滚柱沿丝杠轴线呈圆周状均匀分布。

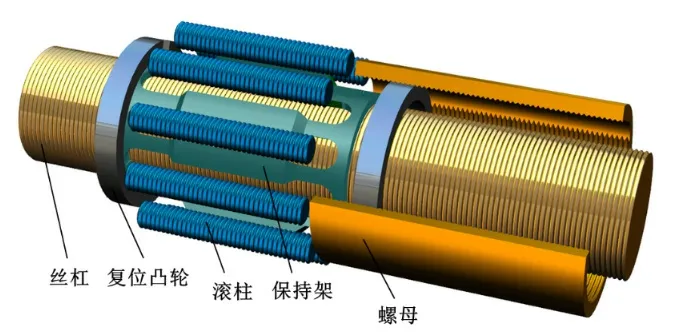
图1 循环式行星滚柱丝杠副结构图

当滚柱完成一个周期的转动后，在保持架内到达极限位置，正好对应螺母内部的让位槽位置处，同时螺母端部固定的复位凸轮使滚柱复位，回到起始的位置，使滚柱实现往复循环运动。在复位过程中，滚柱始终与螺母的让位槽处啮合。标准式行星滚柱丝杠副是将空间运动等效为行星齿轮传动机构运动的平面机构[13]。

循环式行星滚柱丝杠副则是在标准式行星滚柱丝杠副的基础上进行演化，丝杠1视为太阳轮，滚柱2视为行星轮，螺母3视为中心轮，保持架H视为行星架，复位凸轮4与螺母3固定。

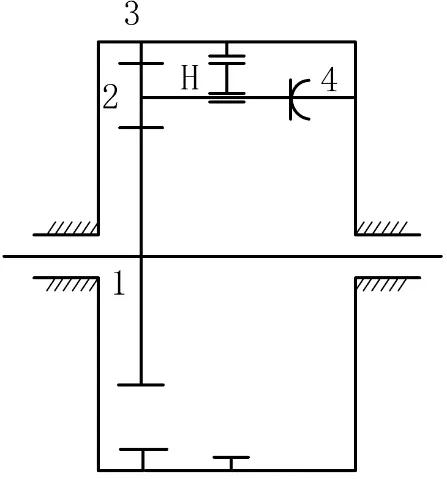
图2 循环式行星滚柱丝杠副平面机构简图

2 循环式行星滚柱丝杠副的自由度计算

为了分析循环式行星滚柱丝杠副的空间运动规律，特进行自由度验算。空间机构的自由度计算一直缺少准确公式，而运用约束螺旋理论[14]定义这些约束能够更加准确的分析自由度，提出了修正的Grübler-Kutzbach 公式。通过修正的 Grübler-Kutzbach 公式计算循环式行星滚柱丝杠副空间自由度，从空间机构学角度验证该机构是否具有确定的相对运动。

2.1 基于约束螺旋理论的自由度计算

2.1.1 修正的G-K公式

通过修正的G-K公式[15]进行计算，确定冗余约束和局部自由度，可以求得循环式行星滚柱丝杠副的自由度。

式中，M为机构的自由度，d为机构的阶数，n为机构中的构件数（包括机架），g为运动副的个数，fi为第i个运动副的自由度，v为冗余约束的个数，ζ为机构中的局部自由度。

2.1.2 空间自由度计算方法

1）建立Plücker坐标；

2）依次将每个运动副具有的自由度表示为对应的运动旋量＄i；

3）将运动旋量＄i整理为运动旋量系A；

4）对运动旋量系A求反螺旋，求解得到约束反螺旋系B，反螺旋系B的秩就是该空间机构的公共约束数；

5）判断该空间机构是否存在冗余约束、局部自由度；

6）代入修正的G-K公式求解。

本文通过建立循环式行星滚柱丝杠副的空间简图，基于约束螺旋理论，通过以上的方法计算和分析循环式行星滚柱丝杠副的自由度。

2.2 循环式行星滚柱丝杠副的空间自由度分析

循环式行星滚柱丝杠副中复位凸轮除了充当挡圈的作用，还有使滚柱回程的作用，复位凸轮固定在螺母内，循环式行星滚柱丝杠副空间机构简图如图3所示。

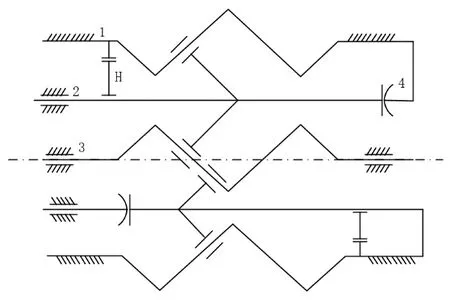
图3 循环式行星滚柱丝杠副空间简图

因为为行星滚柱丝杠对称布置，简化计算机构简图为单滚柱、单复位凸轮的情况，如图4所示，电动机带动丝杠旋转，丝杠轴线方向为plücker坐标轴的z方向。

图4 循环式行星滚柱丝杠副空间部分图

其中各元件对应的运动旋量系A的坐标矢量表示如下：

螺母—保持架 ＄1=（0 0 1;p10 0）

滚柱—保持架 ＄2=（0 0 1;p20 0）

螺母—滚柱 ＄3=（0 0 1;p3q3r3）

滚柱—凸轮 ＄4=（0 0 1;p4q4r4）

丝杠—滚柱 ＄5=（0 0 1;0 0 r5）

丝杠—机架 ＄6=（0 0 1;0 0 r6）

螺母—机架 ＄7=（0 0 1;p70 r7）

其中，pi和ri为不同的实数，这个运动旋量系中的5个旋量坐标线性无关，观察这个机构，求取各个分支的约束螺旋系，约束螺旋系B为：

＄r11=(0 0 0;1 0 0)

＄r12=(0 0 0;0 1 0)

这两个约束力偶有2个公共反螺旋，即机构有2个公共约束，则λ＝2，而d=6-λ=4。该机构不存在冗余约束，ν＝0。该机构也不存在局部自由度，ζ＝0。

将以上数值代入如式(1)所示的修正G-K公式，求得自由度为：

得到循环式滚柱丝杠副的自由度为1。这与实际运动相符，即丝杠的转动带动滚柱做行星运动，滚柱的行星运动最终转换为螺母的直线平动，验证了循环式行星滚柱丝杠副具有确定的相对运动。

3 循环式行星滚柱丝杠副的运动分析及导程计算

在循环式行星滚柱丝杠副运动过程中，丝杠转动，滚柱绕着丝杠公转以及绕着自身轴线自转，滚柱带动螺母沿着轴线方向移动，由于螺母周向固定，螺母只沿轴线方向移动不转动。

首先分析循环式行星滚柱丝杠副各构件的运动关系，丝杠和螺母的旋向均为右旋，如图5所示，点O为滚柱的中心，点Os为丝杠和螺母的中心。rs、rR、rN分别为丝杠、滚柱、螺母的螺纹中径的半径。点B为滚柱和螺母的啮合点，点A为滚柱和丝杠的公共啮合点。丝杠以ws的角速度逆时针公转，丝杠通过摩擦带动滚柱以角速度wr自转，以角速度wR公转。

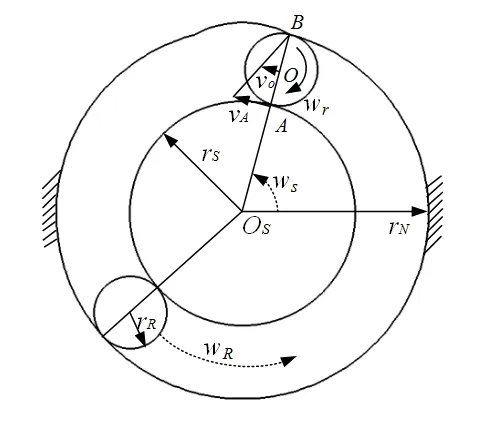
图5 循环式行星滚柱丝杠副的运动简图

忽略滑动的存在，螺母由于周向固定，滚柱和螺母之间的运动为纯滚动，接触点B处是绝对瞬心点。而滚柱和丝杠接触点A处速度相等，接触点A的速度可以表示为：

由图5几何关系可知：

式中：OB=rR，AB=2rR。

结合式(3)、式(4)有：

滚柱中心点的速度vO可以表示为滚柱公转半径与滚柱公转角速度的乘积：

由于接触点B是绝对瞬心点，可表示为滚柱绕瞬心点B旋转，所以vO可以表示为：

则滚柱自转角速度wr为：

结合式(5)和式(6)，滚柱的公转角速度为：

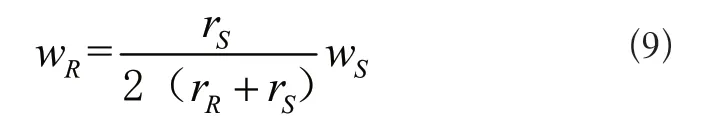
由式(9)可知，滚柱的自转和丝杠的公转方向相反，当右旋丝杠逆时针方向转时，滚柱顺时针方向自转，但由于滚柱为无螺旋升角的环槽状，其自转不会改变自身相对于丝杠螺旋线的位置，不影响丝杠和滚柱的相对位置。同时，滚柱逆时针公转与丝杠的转动方向相同。

则螺母沿轴线的移动速度v为：

式中，PS为丝杠的导程。

循环式行星滚柱丝杠副的实际导程P为：

结合式(9)、式(10)和式(11)有：

由式(12)可得循环式行星滚柱丝杠副的实际导程P小于丝杠的导程PS。在实际工作情况下，由于滚柱无螺旋升角，丝杠与滚柱在接触位置会产生相对滑移，实际导程大小处于P和PS之间。因此，循环式行星滚柱丝杠副在工作时，必须事先施加足够的预紧力，为接触区域提供足够的摩擦力，尽可能的避免明显的滑动现象发生，以提高循环式行星滚柱丝杠副的可靠性。

4 循环式行星滚柱丝杠副的运动学仿真

4.1 循环式行星滚柱丝杠副的三维模型及处理

基于ADAMS软件，将装配好的循环式行星滚柱丝杠副三维模型导入ADAMS软件，循环式行星滚柱丝杠副的结构参数如表1所示，之后修改材料属性，添加运动副，得到的运动副模型如图5所示。在主动件丝杠上添加驱动，确定其运动规律，设置运动时长5s，步数设置为2500步，模拟循环式行星滚柱丝杠副的实际工作情况。

图5 循环式行星滚柱丝杠副的运动学模型

表1 循环式行星滚柱丝杠副的结构参数

4.2 仿真结果与分析

1）取一个滚柱为例说明循环式行星滚柱丝杠副运动学仿真中滚柱的仿真结果，图6分为滚柱在x、y轴上的位移曲线图，由图可知，滚柱在x、y轴方向进行周期性旋转运动，可以从图6中得到曲线的波峰和波谷之间的距离得到滚柱绕丝杠的公转直径为30.5mm，图7为滚柱在和z轴上位移曲线图，滚柱在z轴方向自转一周是1mm，得到滚柱绕丝杠轴线做公转运动的同时绕自身轴线自转，这个结果与理论设计值一致。

图6 滚柱在x、y轴上位移曲线图

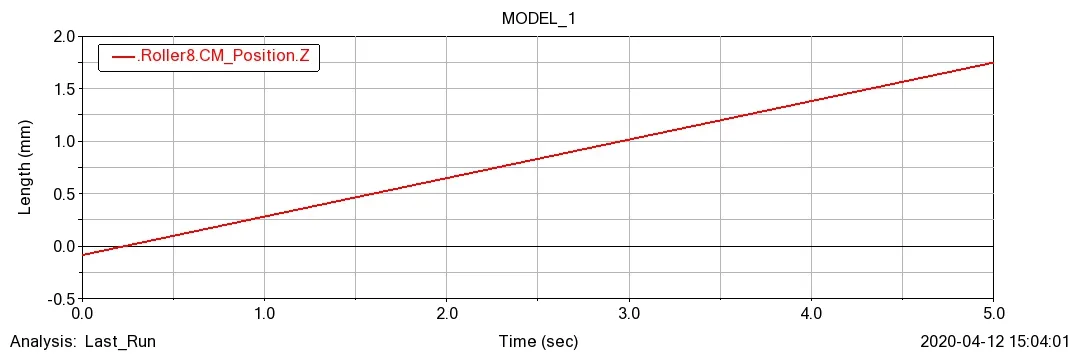
图7 滚柱在z轴上位移曲线图

如图8所示为滚柱在x、y轴方向上的速度曲线图，曲线图表明滚柱在在x、y轴方向速度呈周期性变化，与位移曲线图所得出的滚柱在x、y轴方向做周期性运动结果一致。如图9所示，滚柱在z轴方向上以恒定速度值运动，表明滚柱在z轴方向做匀速直线运动。

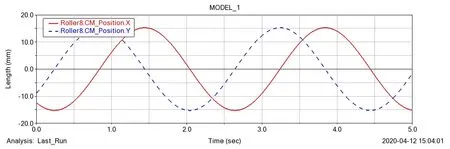
图8 滚柱在x、y轴上速度曲线图

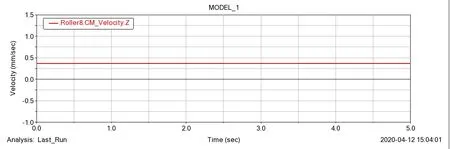
图9 滚柱在z轴上速度曲线图

2）丝杠在x、y轴和z轴上的位移曲线图如图10所示，由图可知，丝杠在x、y轴位移为0，在z轴方向上的位移值为恒定值，所以丝杠在x、y轴和z轴方向上相对位移。

图10 丝杠在x、y轴和z轴上位移曲线图

由图11可知丝杠在x、y轴的速度为周期运动，由图12可知丝杆的角速度值恒定不变，表明丝杠绕自身轴线方向做回转运动。

图11 丝杠在x、y轴和z轴上速度曲线图

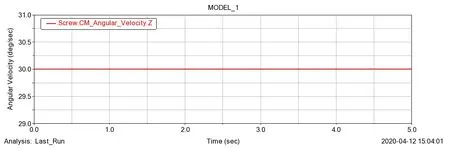
图12 丝杠角速度曲线图

3）螺母在x轴、y轴和z轴上的位移曲线图如图13所示，由图可知，螺母在x、y轴相对位移值恒为0，螺母在z轴方向上的位移曲线与滚柱在z轴方向上的位移曲线平行，说明螺母与滚柱在z轴方向运动状态一致。

图13 螺母在x轴、y轴和z轴上位移曲线图

螺母在x轴、y轴和z轴上的速度曲线图如图14所示，由图可知，螺母在x、y轴方向速度恒为0，螺母在z轴方向的速度为恒定值，表明螺母的运动沿z轴方向的匀速直线运动。

图14 螺母在x轴、y轴和z轴上速度曲线图

综上所述，基于ADAMS软件进行循环式行星滚柱丝杠副的运动学分析，分析了丝杠、滚柱、螺母的位移和速度曲线图，仿真结果与工作原理一致。

5 结语

1）通过建立循环式行星滚柱丝杠副的空间机构简图，基于约束螺旋理论计算，该空间机构的输出为沿轴线方向的自由度为1的移动，验证了该机构具有确定的相对运动。

2）对循环式行星滚柱丝杠副的运动参数与实际导程进行理论分析，根据各构件间的运动关系进行理论推导，对循环式行星滚柱丝杠副的实际导程进行了计算，得出实际工况下，循环式行星滚柱丝杠副的滚柱和丝杠在接触区域会发生滑动，所以要施加有效的预紧力，使丝杠和滚柱接触区域产生摩擦力，减少滑动现象。

3）基于ADAMS软件进行了循环式行星滚柱丝杠副的运动学分析，仿真结果与工作原理和运动学理论分析相符，验证了循环式行星滚柱丝杠副工作原理的合理性。