基于启发式算法的集装箱甩挂运输任务集调度优化

王吉生，罗志勇

（1.南昌交通学院，南昌 330100；2.中国铁路北京局集团有限公司丰台货运中心，北京 102300）

0 引言

甩挂运输是指在牵引车与挂车在自由搭配的环境中，牵引车拖带挂车至目的地将挂车甩下后，拖挂新的挂车或者不挂任何挂车运往另一个目的地的运输组织方式。甩挂运输充分发挥了并行工作的优势，大大缩短了牵引车等待货物装卸及在物流中心排队的时间，从而使得牵引车的作业效率明显提高。

目前，相关学者设计了许多关于甩挂运输方面的研究成果。如王天予[1]等人分析了仿真技术实施甩挂运输优化。谷首更[2]在贪婪算法的基础进行优化改进，针对港口集装箱的运输需求，建立了对应的调度模型。王宝远[3]分析甩箱运输成本组成以及特点，选取甩箱运输成本、时效性2个主要因素为研究对象，确定甩箱运输模式配送成本最低的目标优化模型。

然而，现有文献中的优化算法很少将任务的时间紧迫度考虑在内。为此，本文以苏宁物流中心为例，基于时间紧迫度来优化甩挂运输牵引车调度，利用启发式算法求解在最短的时间内完成已知任务的模型已知任务在最短时间能够完成的目标进行求解。

1 问题描述

设轴辐式物流网络图G=(V,A)，其中，V={0,1,...,n}，点0为物流运输的甩挂中心，1,...,n表示不同任务节点。A表示点1,...,n之间的距离弧集。具体的结构图如图1所示。

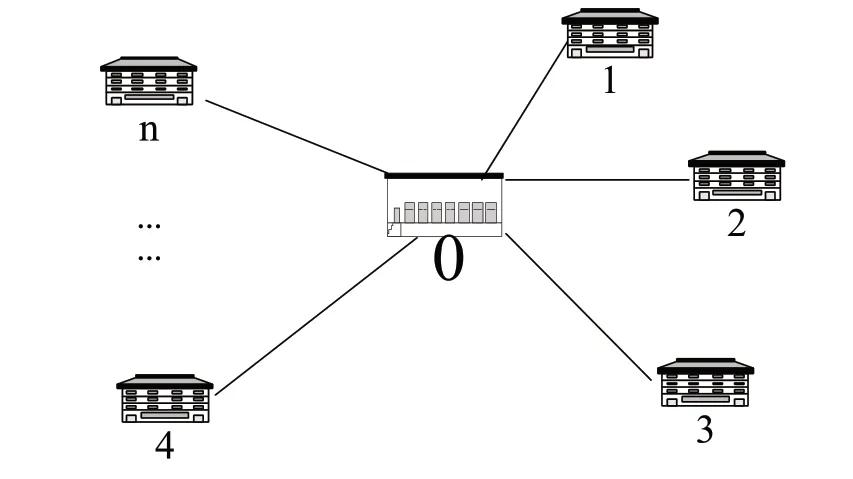
图1 轴辐射子网络图

图1中，0为甩挂中心，1到n为与甩挂中心进行货物运送衔接的点即客户节点。每天牵引车都需从图中的0点即配送中心点出发，去取箱子或者是送箱子，这一任务称为取箱任务或者送箱任务。取箱任务为在1到n点有已经装满好货物的挂车，牵引车立刻过去把挂车挂上，把它运回到0点甩挂中心。送箱任务为在1到n点有货物需要装载，牵引车马上挂上空的挂车即空箱去需要装载货物的客户点，放下空的挂车去下一个任务点完成其他的事情，当这个需要装载货物的客户点把货物装好后，那么这个客户点就变成新的取箱点。

每一次执行任务，牵引车的出发点都是不确定的[4]。若上次的任务是取箱，那么牵引车的出发点就是0点即甩挂中心；若上次的任务是送箱，那么牵引车的出发点就是在上次任务客户点。

根据任务点的需求，在上一个任务和下一个任务的设置中，可以把牵引车的行驶路径分为四类：

1）上一任务是取箱任务，下一任务是取箱任务；

2）上一任务是取箱任务，下一任务是送箱任务；

3）上一任务是送箱任务，下一任务是取箱任务；

4）上一任务是送箱任务，下一任务是送箱任务。

这四类路径类型如图2所示。

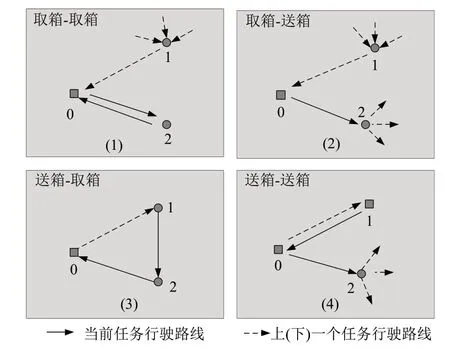
图2 四种车辆路径类型

图2中，0为甩挂中心，1和2均为客户需求点。实线箭头为加入本次路程计算的路线，虚线箭头为上（下）一个任务行驶路线，即不加入本次路程计算的路线。牵引车在途行进的全程路线由该四种类型路线连接而成[5]。

本论文考虑甩挂运输任务量均源于一个物流园区，所有的发货货物均需在甩挂中心集货后再发往下一个途经点，所有收货货物也均需先运到某城市的甩挂运输中心后再分送到各个收货点。假设先规定每个任务完成需要的时间，再开始安排所有的调度工作，现仅考虑用一辆牵引车行驶完成所有任务，求完成总时间最短的方案。

2 集装箱甩挂运输任务集调度优化的混合整数规划模型

2.1 假设条件

根据物流园区实际运转情况，作出以下假设:

1）所有牵引车和挂车都采用统一标准尺寸；

2）一辆牵引车一次只拖挂一辆挂车；

3）牵引车拖挂重箱和拖挂空箱的速度相同；

4）牵引车拖上挂车以及取下挂车的时间不计；

5）牵引车每天从甩挂中心出发，最后返回到甩挂中心。

2.2 符号定义

模型中的符号定义如下：m1表示第一种路径类型的任务数；m2表示第二种路径类型的任务数；m3表示第三种路径类型的任务数；m4表示第四种路径类型的任务数；M表示所有任务集合，且满足M=m1∪m2∪m3∪m4；tij表示i到j的行驶时间与在j地的等待时间之和，则存在：

2.3 模型建立

目标函数表示为：

约束条件表示为：

式中，t1表示完成从甩挂中心出发的取箱任务的所需时间；t2表示完成从甩挂中心出发的送箱任务所需的时间；t3表示完成从任务节点出发的取箱任务所需的时间；t4表示完成从任务节点出发的送箱任务所需的时间；mint表示完成总时间最短的目标函数；式(4)表示每个任务仅且只被完成一次；式(5)表示任务行驶路线决策变量的0～1约束。

3 基于时间紧迫度的启发式算法

本文根据每个任务的时间紧迫度选择下个执行任务，紧迫度Em由公式得出。在每执行完一个任务之后都更新剩余未完成任务的时间紧迫度，在这些剩余未完成的任务中，优先完成紧迫度最高的，图3为算法流程图。

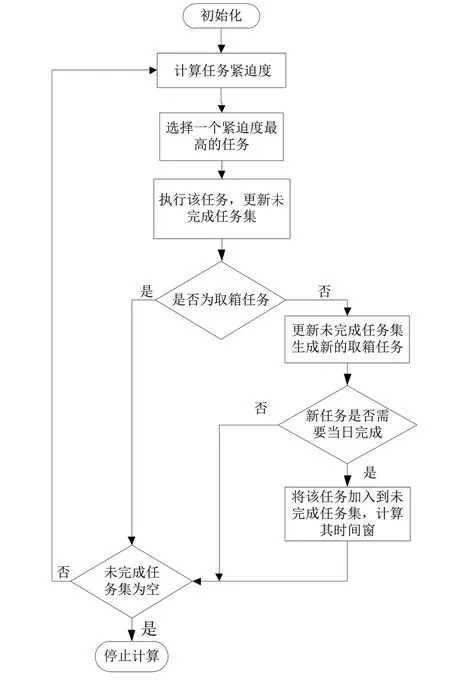
图3 启发式算法流程图

具体实际操作步骤进行如下：

Step1：初始值：完成所有任务的总时间t=0，未完成任务集L=M，根据送箱任务转化而来的取箱任务数i=1，进入step2；

Step2：计算所有未完成任务的时间紧迫度Em=a-(ETm-Tnow)，m∈L,其中a为一常数，在本文中将设a=10，ETm设置为任务m的最早开始时间，Tnow为当前时间，进入Step3；

Step3：选择一个执行任务next_m=max{Em,m∈M}。

Step3.1：如果next_m∈Q，把完成任务next_m所需的时间加入到t中，L=L/next_m，进入Step4；

Step3.2：如果next_m∈S，在t中加入完成任务next_m所需的时间，L=L/next_m，一个新的取箱任务qm+i将产生，然后再判断此次取箱任务是否需要在当日完成，若是，则把qm+i的时间窗计算出来，本文最早开始时间设置为ETqm+i=任务next_m的执行时间+装卸时间，最晚开始时间设置为LTqm+i=ETqm+i+1小时，否则不考虑该新的取箱任务，进入Step4；

Step4:判断确定L集合是否为空，如果为空，停止计算，输出t和行驶路线，如果不为空则转到Step2。

4 数值检验

本文以苏宁南昌物流中心为例，苏宁南昌物流中心为F0，选定其辐射的五个客户点F1、F2、F3、F4、F5提供服务。表1的数据表示客户点与客户点间的距离和牵引车到达各个客户点所花费的时间，具体如表1所示。假设牵引车在行驶的过程中是匀速的，且速度设为每10分钟行驶的距离为5个单位距离。表2的数据表示各个客户点需要牵引车完成的所有任务量，具体如表2所示。每项任务的时间窗口如表3所示。

表1 节点之间距离和车辆所用时间

表2 各节点作业量

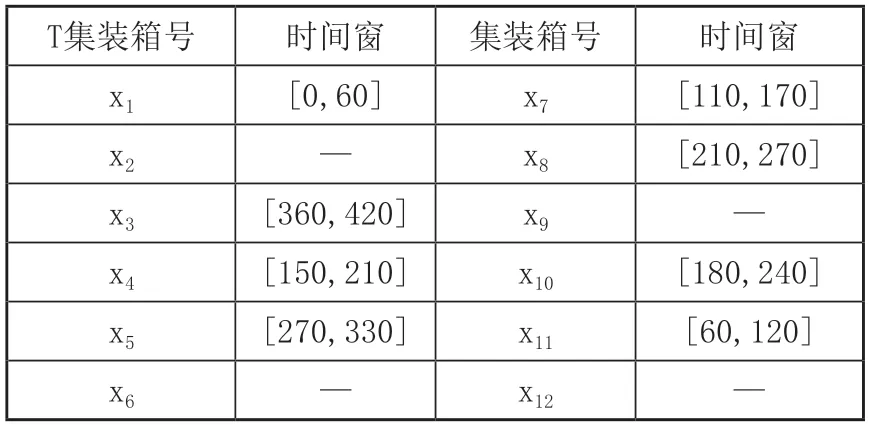
表3 每个任务对应的时间窗

在所有集装箱号的列表里，其中x2、x6、x9、x12是从送箱任务集装箱号x1、x4、x7、x10衍生出来的，所以x2、x6、x9、x12时间窗均是不确定的。为方便计算，假设把在客户点F1、F2、F3、F4、F5的进行装箱作业，8个小时均能完成，如果特殊情况，可延长1个小时；在每天的运输行驶过程中，假设牵引车的运输作业时间是早上6点，排除车辆限行情况。由于客户要求将从集装箱x3和x8派生的取箱任务安排在第二天进行运输，因此，从集装箱 x3和x8派生的取箱任务在本研究中不予考虑。

牵引车途径各点的时间统计结果如表4所示。

表4 牵引车途径各点的时间

表5为每个任务的最优形式路线、所属类型及其被完成的顺序。表6为牵引车开展送箱任务时派生出的取箱任务及其派生任务时间窗。表7为完成各项任务之后重新计算出来的所有任务的时间紧迫度，然后选取其中时间紧迫度最高的一项作为下一个马上要执行的任务。

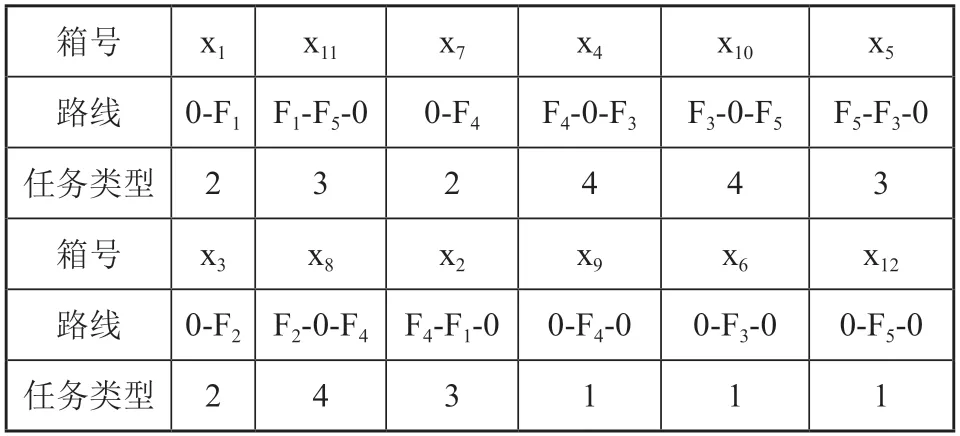
表5 每个任务的所属类型及其被完成顺序

表6 派生任务及其时间窗

表7 每步的所有任务紧迫度

由此可得，若在甩挂运输的基础上结合合理的运输调度方式，从早上6点到晚上6点30分即可完成所有任务；反之用传统方式，且同样牵引车每天从早上6点开始发车，每个集装箱的货物装载作业时间为7小时，那么每天最多能够完成的运输任务仅仅只有两个。即本文的四个任务（两个送箱任务和两个取箱任务），而采用根据时间紧迫度的需求进行的甩挂运输调度能够使得十二个任务点得以完成。因此，合理的甩挂运输作业调度比传统的运输效率提高近3倍。

5 结语

本文以苏宁物流中心为例，运用轴辐式网络集装箱甩挂运输结合每个任务的时间紧迫度性的要求，以完成所有任务的总时间最短为目标建立了优化模型，设计了基于时间紧迫度的启发式算法求解，对多个任务进行调度优化，合理安排完成任务调度的先后顺序，通过数值检验的方式，得出通过甩挂运输调度的方式，苏宁物流中心的甩挂运输作业对任务集进行调度优化比原有的运输效率提高近3倍，减少了牵引车在各个客户点完成装卸的等待时间，同时也减缓了空车行驶的概率，为苏宁物流公司的货物运输提供一些更加科学合理的优化调度方法，实现提高物流中心作业效率，降低成本的效果。