基于类间距的径向基函数－ 支持向量机核参数评价方法分析

宋小杉，蒋晓瑜，罗建华，姚军

(1.装甲兵工程学院 控制工程系，北京100072;2.装甲兵工程学院 科研部，北京100072)

0 引言

支持向量机(SVM)由Vapnik 于1995年提出［1］，是一种智能学习机器，相对于人工神经网络，具有3 个优点:1)SVM 以统计学习理论为基础，从结构风险最小理论和VC 维理论发展而来，具有完善的理论基础;2)SVM 同时考虑了经验风险最小和学习机器的复杂度，并进行了恰当的折中，使其具有了很好的泛化能力;3)SVM 算法是一个凸二次规划问题，因此具有全局最优解。正是由于这些优点，十几年来，人们对SVM 的研究一直非常活跃，从理论到应用被人们不断完善和扩展。

导致SVM 得到广泛应用的另一个原因是核函数的引进。核函数的引进有2 个好处:1)将样本空间中线性不可分的样本映射到更高维的特征空间中，使其线性可分;2)通过核函数用原空间中的运算实现更高维的特征空间中的运算，避免了“维数灾难”问题。

常用的核函数有以下几种

1)高斯径向基函数(RBF):K (x，x')=exp(－γ‖x－x'‖2);

2)q 阶多项式函数:K(x，x')=［γ(xT，x')+b］q;

3)感知器核函数:K(x，x')=tanh［γ(xT，x')+b］;

4)B 样条函数:K(x，x')=B2n+1(x－x');

其中RBF 核具有较少的参数和广泛的普适性，在SVM 的应用中是首要选择［2］。本文只针对RBFSVM 进行了研究。核函数选定后的首要工作是参数选择，参数选择的优劣直接影响SVM 判别模型的泛化能力，是研究SVM 的重要内容，也是SVM 的研究热点［1－10］。SVM 参数选择最基本的方法是网格搜索法［1－2］，下文将详细介绍。张学工等人最早将SVM 引进国内，2002年提出了基于变异函数的RBF参数估计方法［3］;2005年，Ayat［4］提出了一种基于SVM 分类错误概率估计的SVM 性能评价准则，并与GACV 和VC 维准则进行了比较，显示了该方法选择参数的有效性，但该方法实现较为复杂;近几年，人们将遗传算法和粒子群算法应用到SVM 参数选择中［5－8］，文献［9］将参数选择看作非线性动态系统，利用扩展卡尔曼滤波算法进行选择，这些算法均得到了较好的结果，但它们并没有从参数本身的性质以及参数在SVM 中的本质作用入手来研究，所以都存在一定的局限;文献［10］通过比较特征空间中5 种不同的距离定义式，指出了类中心之间的2范数距离最能有效估计SVM 判别函数的泛化性，并基于类中心距选择核函数，但该文对类中心距的应用缺乏理论推导和深入分析。本文分析了RBF 核参数γ 对空间映射结果的影响，从分析结论中得到了基于ICMD 的核参数γ 评价方法，并从理论和实验两方面对该方法进行了深入分析，证明了该方法是1 种既有效、又省时的参数选择方法。

1 SVM 原理

给定训练样本集:{(xi，yi)，i =1，2，…，l}，其中xi∈Rn，yi∈{1，－1}代表类别，l 为样本集中样本总数，则SVM 的原始优化问题为

式中:w 是SVM 决策函数的法向量，ξi称为松弛变量，是SVM 分类间隔软化的标志，意味着可以存在被超平面错分的样本，C ＞0 是一个自定义的惩罚因子，控制着对错分样本的惩罚程度。

引入拉格朗日乘子法，得其对偶优化问题为

对(2)式求解得到SVM 判决函数

可以看出，SVM 的实质是一个非线性空间的线性分类器。它首先通过核函数将样本空间中的样本向量映射到更高维数的非线性空间，然后在此非线性空间寻求一个最优线性的分类超平面。其结构示意图如图1所示。所以SVM 的参数选择也可以分为两步，首先是核参数的选择，核参数影响着对样本空间的映射结果和特征向量在特征空间中的分布;其次是惩罚因子C，C 影响着SVM 决策函数对特征向量的错分程度，C 越大，越不允许错分。

图1 SVM 结构示意图Fig.1 Schematic diagram of the SVM structure

2 RBF 核参数对空间映射的影响

定义1:(核函数)设χ 是Rn中的一个子集，称定义在χ×χ 上的函数K(x，x')是核函数，如果存在着从χ 到某一个Hilbert 空间H 的映射

使得

其中(，)表示H 中的内积。

在特征空间中可以分别用内积和L2范数来衡量两个向量之间的夹角和距离，所以有下面定理。

定理1:设Θi，j表示Hilbert 空间H 中任意两向量Φ(xi)和Φ(xj)之间的夹角，则有

证明略。

定理2:设Di，j表示Hilbert 空间H 中任意两向量Φ(xi)和Φ(xj)之间的距离，则有

证明略。

把RBF 表达式分别代入(4)式和(5)式，得到经RBF 核映射的特征空间中任意两向量Φ(xi)和Φ(xj)之间的夹角和距离分别是

和

从(6)式和(7)式可以看出，在RBF 所映射的空间中，γ 是唯一的参数，调节γ 的大小可以隐含地影响所映射的特征空间，以及特征向量在其中的分布。下面研究γ 对这对样本映射结果的影响。

在样本空间中，任意选取一对xi，xj，总存在ε ＞0，使得‖ xi－xj‖2≤ε.也就是说，样本空间中两向量之间的距离是个有限的实数。那么，在(6)式和(7)式可以中考虑两种极限情况:

1)当γ→0 时，一方面cosΘi，j→1，从而Φ(xi)和Φ(xj)之间的夹角Θi，j→0，另一方面Φ(xi)和Φ(xj)之间的距离Di，j→0.说明当γ→0 时，RBF 核将样本空间映射到了一个0 维点;

2)当γ→∞时，一方面cosΘi，j→0，从而Φ(xi)和Φ(xj)之间的夹角Θi，j→π/2，另一方面Φ(xi)和Φ(xj)之间的距离Di，j→说明当γ→∞时，RBF核将样本空间映射到了一个l 维的空间，在这个空间特征向量两两正交，且每两个特征向量之间的距离相等，这意味着在以距离和角度为相似度度量的特征空间里，所有Φ(xi)被同一化了。

γ 对映射结果的影响曲线如图2所示。图2显示了γ 对映射结果影响的单调性，从而可以得出下面3 个结论

1)随着γ 的增大，经RBF 映射的特征空间的维数(FSD)单调增大。γ→0 时，FSD→0，γ→∞时，FSD→l.其中l 是样本空间中样本的个数。

图2 γ 对映射结果的影响Fig.2 Effects on the mapping space by γ

2)随着γ 的增大，经RBF 映射的特征空间中各向量之间的夹角Θi，j单调增大。γ→0 时，Θi，j→0，γ→∞时，Θi，j→π/2.

3)随着γ 的增大，经RBF 映射的特征空间中各向量之间的距离Di，j单调增大。γ→0 时，Di，j→0，γ→∞时，Di，j→

3 核空间中的类间距

令m1和m2分别表示核空间中第一类样本和第二类样本的中心向量

其中，l1和l2分别表示第1 类和第2 类的样本个数，l1+ l2= l，x()i和x()i分别表示原空间中第1 类和第2 类中的样本向量，那么核空间类间平均距表达式为

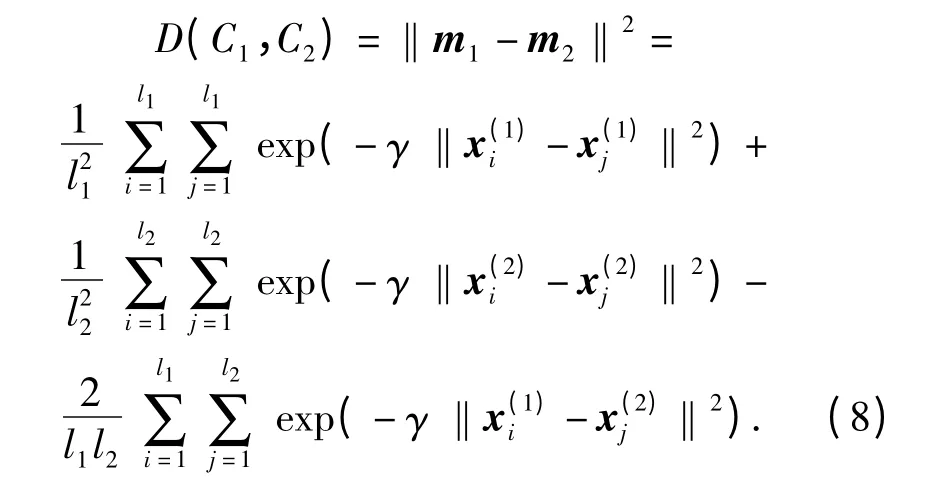
核空间类间角余弦值表达式为

核空间类内角余弦值表达式分别为

将(9)式、(10)式和(11)式代入(8)式得

可以看出类间平均距是类间角和类内角的一个综合度量，当类间角较大、类内角较小时，D(C1，C2)取得较大值，反之则取得较小值。但由(9)式、(10)式和(11)式知，当特征集不变时，类间角和类内角均随着核参数γ 的增大单调增大，那么类间平均距会不会也随着核参数γ 的单调变化，是否存在一个核参数γ0，使得类间平均距达到最大。

由(8)式知，类间平均距与核参数γ 和特征向量xi，(i =1，2，…，l)有关，当特征集不变时xi不变，则类间平均距只与核参数γ 有关，令

有下面定理。

定理3:当γ∈［0，∞)时，J(γ)存在极大值。

证明:J(γ)在［0，∞)区间连续、在(0，∞)区间可导，又，由罗尔定理知必有ξ∈(0，∞)，使得J'(ξ)=0，即J(γ)存在极值J(ξ).

假设J(ξ)是极小值，则J(ξ)＜J(0)=0，但由J(γ)的定义知，当γ∈［0，∞)时J(γ)≥0.

所以假设不真。

所以，当γ∈［0，∞)时，J(γ)存在极大值。

证毕。

由定理3 知，虽然类间角和类内角均随着核参数γ 的增大单调增大，但它们增大的幅度不同，在［0，∞)上存在一个核参数γ0，使类间平均距达到最大，这时核空间特征向量可分性也达到最好［12］。

为了清楚地观察γ－J(γ)之间的关系，我们对从加州大学UCI 网站下载的公开实测特征数据库［7］Heart、Australian、German 和Vehicle、Satimage分别作了γ－J(γ)曲线，如图3所示。γ 的取值为γ={2－15，2－14，…，210}.

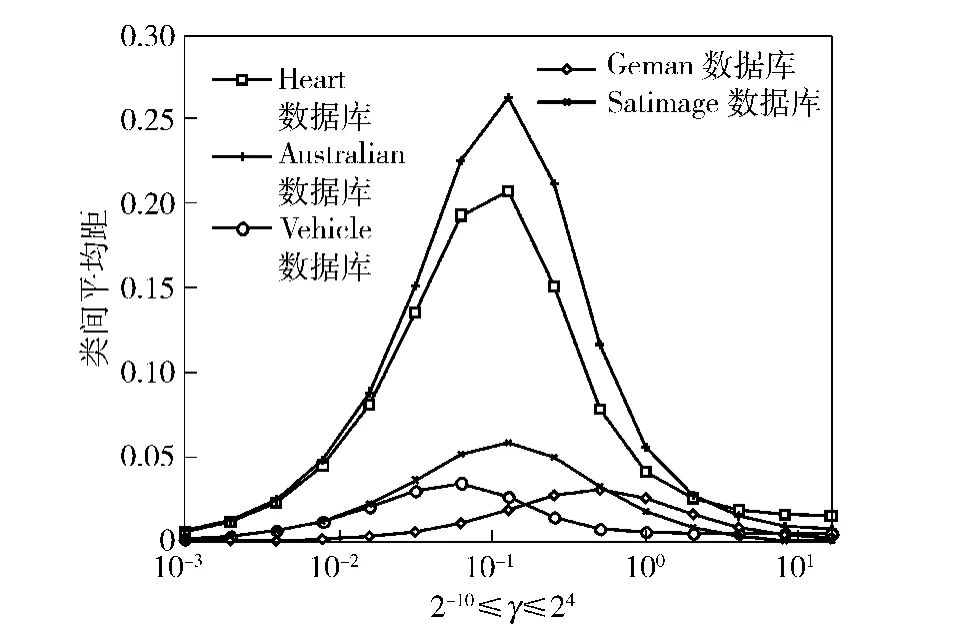
图3 5 个样本集的γ－ J(γ)曲线Fig.3 γ－ J(γ)Curves of 5 sample sets

Heart、Australian、German 数据库中含有2 个类，而Vehicle 中含有4 个类，Satimage 含有6 个类。对多类数据，我们采用一对一计算策略。设数据库中总共有N 个类，一对一计算策略就是从N 个类中依次取出2 个类进行计算，得到N × (N－ 1)/2 组J(γ)，用所有J(γ)的平均值作为最终结果。由图3可以看出，对于这5 个样本集，曲线均在一定的γ值处达到了最大，这5 个γ 值就是5 个样本集对应的最优核参数值。

4 RBF-SVM 参数选择实验

本文提出的核参数评价方法使得可以把(C，γ)分开来选择。首先基于ICMD 得到最优γ 值，在此基础上，基于10－折交叉验证选择最优的C 值，我们称之为“两步法”。10－折交叉验证是一种经典的SVM 性能评价准则，它首先把l 个样本随机分成10个互不相交的子集，即10－折S1，S2，…，S10，每个折大小大致相同。共进行10 次训练与测试，第i 次的做法是，选择Si为测试集，其余S1，…，Si－1，Si+1…，S10的合集为训练集，算法根据训练集求出判别函数后，即可对测试集Si进行测试。记其中错误分类的样本数为li，10 次迭代完成后，便得到了l1，…，l10.10－折交叉验证就是把10 次迭代的平均误差作为SVM 性能评价准则。为穷极搜索范围，C 的取值集合为{2－10，2－14，…，215}，γ 为{2－15，2－14，…，210}.这样，用两步法在上面的取值集合中完成一次参数选择需要(26 +26 ×10)×l2次迭代运算。

网格搜索法是传统的SVM 参数选择方法［2］。网格搜索法就是把两个参数取值集合中的值两两配对进行10－折交叉验证，使交叉验证错误率最小的参数对(C0，γ0)就是最优参数。研究证明，网格搜索法能够较好的评价SVM 性能，但其时间开销太大，要在上面的取值集合中完成一次参数选择需要26 ×26 ×10 ×l2次迭代运算。

实验数据一部分与上节相同，来源于加州大学UCI 网站的公开实测特征数据库Heart、Australian、German、Vehicle 和Satimage，另一部分则是我们自己建立的小物件特征库和装甲车辆特征库。其中小物件特征库中包含4 类目标，分别是充电器、打火机、瓶盖和钥匙，装甲车辆特征库包含2 类目标，分别是国产某型坦克和某型步战车。每个特征库包含一个训练集和一个测试集，它们是独立同分布的两个数据集，SVM 基于训练集进行训练得到SVM 判别函数，然后在测试集上进行识别测试。实验是在CPU 频率1.7 GHz，内存512 M 的PC 机上用C 语言编程进行的。对含有多类的样本集，采取了一对一的多类分类策略。表1给出了两种方法进行核参数选择的结果。

表1 网格搜索法和两步法进行参数选择结果比较Tab.1 Comparison between the grid search method and the two－stage method

表1给出了对上述对7 个数据库分别用两种方法进行SVM 参数选择的结果，其中，Heart、German、Australian 和装甲车辆均为2 类数据，Vehicle 和小物件均为4 类数据库，而Satimage 则是包含了6 类目标的多类数据，实验对多类分类采取一对一策略。从表1可以看出:1)对所有7 组实验，基于ICMD 的二步参数选择所用运算时间更短、速度更快;2)两种SVM 参数选择结果，对测试集的识别率非常接近，但本文提出的方法用时大大减少;3)本文提出的方法对2 类和多类均适用。说明基于ICMD 的二步参数选择方法是一种既有效省时的好方法。

该结果同时也验证了基于ICMD 方法进行核参数选择的可靠性。

5 结论

参数选择是SVM 研究的重要内容，其结果直接影响着SVM 决策函数的识别能力。本文针对RBFSVM，详细分析了核参数γ 对空间映射结果的影响，得出了3 个重要结论。基于结论提出了一种新的核参数评价方法—最大ICMD 方法，使ICMD 值最大的核参数就是最优核参数。文中对该方法进行了理论分析和实验讨论。该方法使得RBF－SVM 的参数选择可分两步进行:首先基于ICMD 找到最优核参数γ，其次基于10－折交叉验证得到最优惩罚因子C。文中将两步法与传统的网格搜索法进行了实验比较，结果显示两种方法选择均选择出了适当的参数，但前者花费的时间远远小于后者，是一种更适合实际操作的方法。该实验同时也验证了基于ICMD方法进行核参数选择的可靠性。

References)

［1］ Vapnik V.The nature of statistics learning theory ［M］.New York:Springer Verlag，1995.

［2］ Hsu C W，Chang C C，Lin C J.A practical guide to support vector classification［EB/OL］.Available at:http:∥www.csie.ntu.edu.tw/cjlin/ papers/ guide/guide.pdf，2003.

［3］ 阎辉，张学工，马云潜，等.基于变异函数的径向基核函数参数估计［J］.自动化学报，2002，28 (3):450－455.YAN Hui，ZHANG Xue－gong，MA Yu－qian，et al.The parameter estimation of RBF kernel function based on variogram［J］.Acta Automatica Sinica，2002，28(3):450－455.(in Chinese)

［4］ Ayat N E，Cheriet M，Suen C Y.Automatic model selection for the optimization of SVM kernels［J］.Pattern Recognition，2005，38(10):1733－1745.

［5］ Huang C L，Wang C J.A GA－based feature selection and parameters optimization for support vector machines［J］.Expert Systems with Applications，2006，31(2):231－240.

［6］ Yu Q，Zhang B H，Wang J L.Parameter optimization of e－SVM by Genetic Algorithm［C］∥The Fifth International Conference on Natural Computation，Tian Jin:ICNC，2009:540－542.

［7］ Guo X C，Yang J H ，Wu C G，et al.A novel LS－SVM hyper－parameter selection based on particle swarm optimization［J］.Neurocomputing，2008，71(16－18):3211－3215.

［8］ Zhang X Y，Guo Y L.Optimization of SVM parameters based on PSO Algorithm［C］∥The Fifth International Conference on Natural Computation，Tian Jin:ICNC，2009:536－539.

［9］ Mu T T，Nandi A K.Automatic tuning of L2－SVM parameters employing the Extended Kalman Filter［J］.Expert Systems，2009，26(2):160－175.

［10］ Wu K P，Wang S D.Choosing the kernel parameters for support vector machines by the inter－cluster distance in the feature space［J］.Pattern Recognition，2009，42(5):710－717.

［11］ Blake C L，Merz C J.UCI Repository of machine learning databases［EB/OL］.http:∥www.ics.uci.edu/～mlearn/MLRepository.html.2003.