动态三角模糊数互反判断矩阵一致性及修正

刘胜，张玉廷，于大泳

(哈尔滨工程大学 自动化学院，黑龙江 哈尔滨150001)

0 引言

层次分析法(AHP)自T.L.Saaty 教授提出以来，已广泛应用并成为系统建模与评估的重要理论和方法之一［1－3］。但传统的AHP 方法在构造判断矩阵时没有考虑人判断的模糊性和所评估系统的时变性。而实际系统却恰恰是一个时刻变动着的系统。随着人们对复杂系统分析研究的深入，这两个不足之处在一定程度上制约了AHP 方法的应用。

为解决上述不足，许多专家学者进行了研究改进，包括采用模糊区间数［4－6］和动态判断矩阵［7－8］对系统进行评估。但目前对模糊动态区间判断矩阵的研究，包括判断矩阵的一致性检验、矩阵元素修正和权值排序仍不是很成熟。文献［9］研究了区间数互补判断矩阵的一致性问题，但其所考虑的两端点区间数无法表征决策者在判断区间内的偏好信息;文献［10］的基于可能度的排序方法的合理性还有待于进一步验证。并且上述文献中判断矩阵都没有考虑系统的时变性。文献［11］和［12］研究了模糊动态AHP 法，通过构建动态模糊规划模型进行分析。但该方法的计算过程太过复杂，并且仅对判断矩阵的中心值进行调整，缺少一种全局优化的概念。

鉴于此，本文从全局优化角度出发，将动态三角模糊数互反判断矩阵的一致性检验、矩阵元素修正和权值排序作为一个整体考虑，保证在对初始判断矩阵做最小程度修正的基础上使得判断矩阵满足一致性要求，并给出权值排序。并采用小生境遗传算法在提高全局寻优能力的基础上对建立的非线性目标优化函数进行优化求解。

1 判断矩阵及一致性

若a=(al，am，au)，且al、au和am分别为a 所支撑的下界、上界和中值，则称a 为三角模糊数［13］。其隶属度函数为

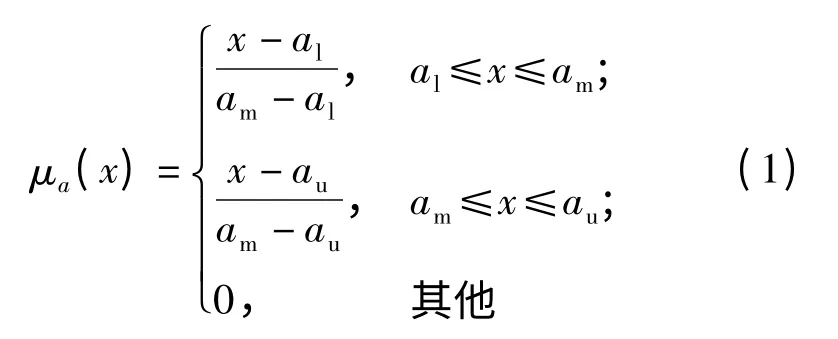
若三角模糊数a 中的元素是一个时变量，则ad=(ald，amd，aud)为动态三角模糊数，如图1所示。动态三角模糊数ad的支撑下界ald、上界aud和中值amd是一个动态值，并且满足

图1 动态三角模糊数Fig.1 Dynamic triangular fuzzy number

动态三角模糊数具有以下运算法则［10］

对有限论域U 中的方案集X，若X 中的动态元素xid和xjd两两对比的偏好信息aijd为动态三角模糊数，则由aijd组成的判断矩阵A =［aijd］n×n为动态三角模糊数判断矩阵。

若动态三角模糊数判断矩阵A =［aijd］n×n中的元素aijd=(alijd，amijd，auijd)满足［11］

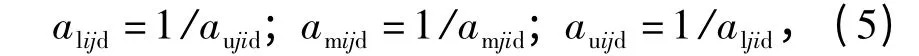
式中，0 ＜alijd≤amijd≤auijd，i，j∈N，则矩阵A 为动态三角模糊数互反判断矩阵。

若互反判断矩阵满足完全一致性，则［3］

式中，ωi为第i 个指标相对于其他指标的重要程度，即为权重。

对动态三角模糊数互反判断矩阵，如果其满足完全一致性，则按照(6)式，以及(3)式和(4)式的动态三角模糊数运算法则，有

(7)式即为动态三角模糊数互反判断矩阵的完全一致性条件。

2 判断矩阵一致性检验、矩阵元素修正及权值排序

2.1 动态三角模糊数互反判断矩阵一致性指标系数

将(7)式的动态三角模糊数互反判断矩阵的完全一致性条件展开，为

定义两个动态三角区间数ad=(ald，amd，aud)和bd=(bld，bmd，bud)的相似度［14］为

式中，s(ad，bd)≥1，s(ad，bd)越小，表示两个动态三角区间数的相似程度越大，当s(ad，bd)=1 时，表示两个三角区间数相等。

因此，如果动态三角模糊数互反判断矩阵满足(8)式的完全一致性条件，则矩阵元素的动态区间数相似度应为1。即

实际上由于系统的复杂性和人们判断的模糊性，(10)式是很难满足的。为使判断矩阵尽可能表征所分析的系统，应该使下式成立

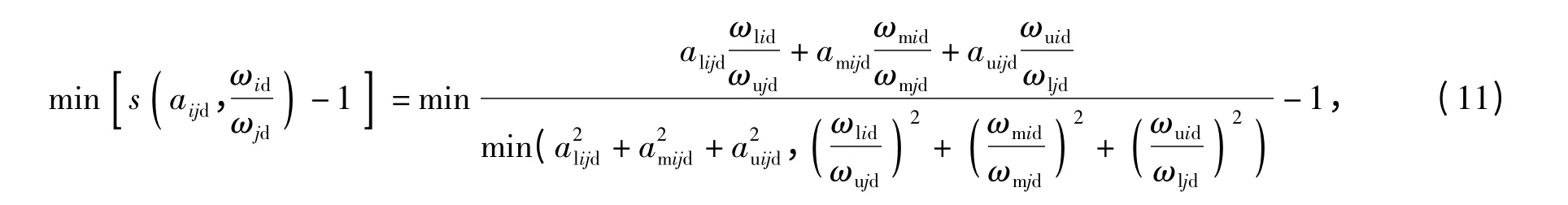
即要使判断矩阵具有满意一致性。

如果判断矩阵不具有完全一致性或满意一致性，则需要对判断矩阵的元素进行调整，使其满足一致性条件。但由于初始判断矩阵中含有专家信息，所以希望最大程度的保留初始判断矩阵中的专家信息，即要对判断矩阵的元素做最小程度的调整。假设初始判断矩阵中的元素为aijd=(alijd，amijd，auijd)，修正后的判断矩阵元素为a'ijd=(a'lijd，a'mijd，a'uijd)，为了对初始判断矩阵的元素做最小程度的调整，修正后的判断矩阵元素和初始判断矩阵元素的动态区间数相似度应最大，即要使得下式成立

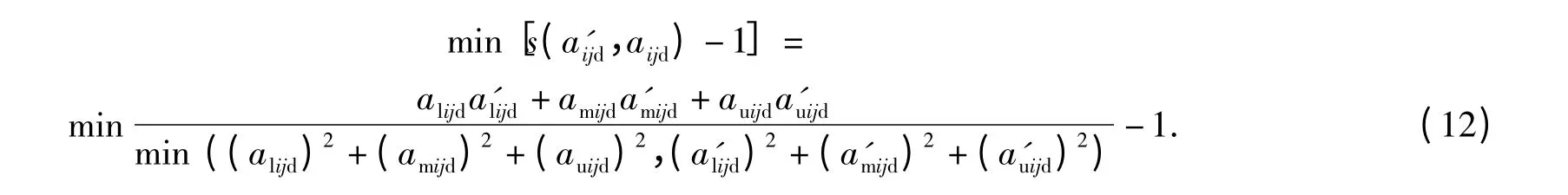
因此，对动态三角模糊数互反判断矩阵进行一致性检验、矩阵元素调整和权值排序时，矩阵元素需要同时满足(11)式和(12)式。反映到整个判断矩阵，则要使下式成立

式中，CIC 为一致性指标系数。

(13)式是一种全局优化模型，将动态三角模糊数互反判断矩阵的一致性检验、矩阵元素修正和权值排序作为一个整体处理，它可以充分利用判断矩阵的信息，在对初始判断矩阵做最小程度修正的基础上使得修正后的判断矩阵满足满意一致性。

采用(13)式计算得到的排序向量也是三角模糊数，即ωi=(ωli，ωmi，ωui).为了对权值进行排序，采用下式［15］进行计算

α 值的选择取决于决策者的风险态度，当α ＞0.5 时，表明决策者追求风险;当α =0.5 时，表明决策者风险中立;当α ＜0.5 时，表明决策者厌恶风险。

采用1～9 标度法，结合(14)式可得到(13)式的约束条件为

1.2.1 循证护理小组 成立循证护理小组，小组成员包括2名主管护理人员、2名资深护理人员以及8名普通护理人员。小组在组建之后要对所有成员采取系统专业的循证护理培训[2]，保证每一位小组成员都能掌握循证护理的相关方法，为循证护理的实施打下扎实基础。

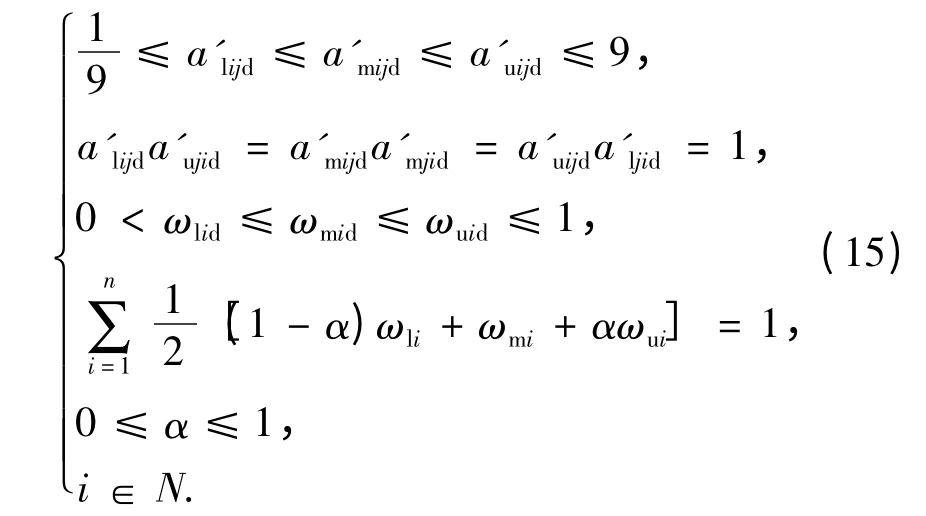
2.2 基于遗传算法的一致性指标系数优化求解

(13)式和(15)式属于非线性优化问题，采用常规方法较难求解，因此考虑采用遗传算法进行优化求解。但简单遗传算法的选择策略由于缺乏多样性保护机制，所以往往收敛于局部最优解［16］。为此，在简单遗传算法的基础上引入小生境技术来提高种群多样性，保证算法寻得全局最优解。

图2是小生境遗传算法的流程图。采用共享函数机制来实现小生境技术。

图2 算法流程图Fig.2 Flow process chart of the algorithm

经过基本遗传算法和记忆得到含有M+N 个个体的新群体，采用下式求出两个个体之间的海明距离

当海明距离小于某一指定距离时，对Xi和Xj中适应度较低的个体处以罚函数。这样适应度差的个体经过罚函数处理后适应度更差，在后续进化中被淘汰的概率也越大。从而达到维护种群多样性和保证个体在约束空间中分散开来的目的。

3 算法分析

3.1 算法复杂性分析

从(13)式中可以看出，随着矩阵维数的增加，所要优化求解的参数个数也随之增多，这必然导致采用遗传算法求解(13)式时种群规模增大，使得计算时间增长。

假设种群规模为n，进行一次选择、交叉和变异的时间分别为te、tc和tm，计算一次适应度的时间为ts，计算一次个体距离的时间为td，做一次罚函数时间为tp，则每一进化代算法的总时间为

如果动态判断矩阵取k 个评估判断时刻，则算法的总时间复杂度为

由于实际应用中，判断矩阵一般不超过9 阶，故各随机构造100 个3～9 阶三角动态模糊数互反判断矩阵，每个判断矩阵取10 个判断时刻，采用(13)式中的模型进行优化计算。算法程序在CPU 时钟频率为3.00 GHz 的计算机上运行，得到每个时刻平均计算时间如图3所示

图3 3～9 阶矩阵运行时间Fig.3 Running time of 3～9 order matrixes

从图3可以看出，计算时间随着矩阵维数的增加而增加。但在矩阵维数不超过9 阶的情况下，本文的计算方法可以满足离线评估判断的要求。对于时变系统的评估，可由评估专家针对系统在不同工作时间、不同工作年限的特性经验给出系统的动态评估判断矩阵，然后采用本文算法进行研究计算。这类系统评估不需要满足实时性要求，故本文离线评估方法在时变系统评估中是可行的。

3.2 算法稳定性分析

将上述各随机构造的100 个3～9 阶矩阵的上三角矩阵任一元素在［aij－βaij，aij+βaij］∩［0，1］内变动，其中β∈［0，1］为相对变动率，判断矩阵下三角元素由(5)式得出。采用(13)式进行排序权值的计算。当β 分别取10%、30%和50%时统计排序权值的最大相对变化率，得到的统计结果如表1所示。

表1 排序权值最大相对变换率Tab.1 Maximum relative change rates of weights

从表1的统计结果可以看出，在β 分别为10%、30%和50%时，排序权值的最大相对变化率在18.2%以内。这表明本文方法在权值排序计算方面具有稳定性。当判断矩阵元素受扰动时，本文方法计算得到的排序权值与原判断矩阵的排序权值十分接近。

3.3 算例分析

以文献［11］中的算例为例进行分析。某市为修筑管路使三个地下水源为三家工厂供水，需探索优化供水方案，以保证使不同时期的供水效益最大。该问题不需要满足在线实时评估要求，可采用离线评估方法解决，本文评估方法的计算时间可满足要求，故可采用本文算法进行分析。限于篇幅原因，仅以政府决策部门给出的各水源地相对工厂1 的动态模糊效益判断矩阵A1(t)为例。

将A1(t)转化为(13)式和(15)式的优化函数和约束条件。采用遗传算法进行优化求解。其中，种群大小为54，按照尺度值的整数部分和随机均匀选择尺度值的小数部分选择父辈，交叉概率为0.8，变异概率为0.05，罚函数为10－5.遗传算法进化60代。决策者风险中立，即α=0.5.当t 取1～10 时，一致性指标系数和权值变化分别如表2和图4所示。

表2 一致性指标系数Tab.2 Consistency index coefficients

从表2中可以看出，当t 从1 取到10 时，一致性指标系数均小于0.1，所以修正后的判断矩阵满足满意一致性要求。图4清晰表现出了三个方案的权值变化情况。

在矩阵修正程度比较中，由于互反判断矩阵的性质，只需比较上三角元素的修正程度。限于篇幅原因，以t 取5 时的判断矩阵为例，初始判断矩阵的上三角矩阵为

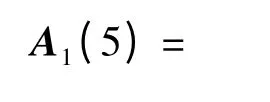
修正后的上三角矩阵为

图4 权重变化Fig.4 Changes of weights

从A1(5)和A'1(5)的对比可以看出，A'1(5)仅对A1(5)中的4 个元素进行了修正，且修正程度分别为0.003 8%、0.005 6%、0.046%和0.004 5%，修正程度很小。

从以上的算例分析可以看出，基于遗传算法的动态三角模糊互反判断矩阵一致性检验、矩阵元素修正和权值排序可以在对初始判断矩阵做很小程度修正的基础上，使得修正后的判断矩阵满足满意一致性要求，并可给出权值排序。与文献［11］相比，本文方法避免了复杂的模糊规划模型的建立和求解，大大降低了排序权值的求解难度。

4 结论

本文对动态三角模糊数互反判断矩阵的一致性检验、矩阵元素修正和权值排序进行了研究。提出的动态三角模糊数互反判断矩阵一致性指标系数函数和基于小生境遗传算法的优化求解方法属于一种全局优化方法，可以在充分利用初始判断矩阵信息的基础上，使修正后的判断矩阵满足一致性条件，给出权值排序。提高了算法的全局寻优能力。对动态系统进行评估是针对给出的动态评估判断矩阵得出在不同工作时刻或不同工作年限时的系统信息，这一过程不必满足在线实时评估的要求，故本文方法对研究离线评估复杂时变系统具有促进意义。

References)

［1］ 杜俊慧，魏法杰.区间数互反判断矩阵一致性及排序［J］.系统工程，2008，26(9):85－88.DU Jun－hui，WEI Fa－jie.The consistency and the priority method of interval number reciprocal judgement matrix［J］.Systems Engineering，2008，26(9):85－88.(in Chinese)

［2］ 高会生，冉静学，孙逸群.基于改进的FAHP 电力通信网风险评估［J］.系统工程理论与实践，2008，28(3):133－138.GAO Hui－sheng，RAN Jing－xue，SUN Yi－qun.Risk evaluation of communication network of electric power based on improved FAHP［J］.System Engineering－Theory ＆ Practice，2008，28(3):133－138.(in Chinese)

［3］ 王有元，周婧婧，陈伟根，等.基于模糊决策的电力变压器风险评估［J］.仪器仪表学报，2009，30(8):1662－1667.WANG You－yuan，ZHOU Jing－jing，CHEN Wei－gen，et al.Risk assessment method of power transformer based on fuzzy decisionmaking［J］.Chinese Journal of Scientific Instrument，2009，30(8):1662－1667.(in Chinese)

［4］ Chen S M.A new method for evaluating weapon systems using fuzzy set theory［J］.IEEE Trans.on System，Man，and Cybernetics－Part A:Systems and Humans，1996:26(4):493－497.

［5］ 文谷生，廖学兵，黄林昊，等.基于模糊综合评估法的某综合信息系统评估［J］.仪器仪表学报，2006，27(6):2338－2341.WEN Gu－sheng，LIAO Xue－bing，HUANG Lin－hao，et al.Evaluation of the integrate information system based on the fuzzy synthetic evaluation［J］.Chinese Journal of Scientific Instrument，2006，27(6):2338－2341.(in Chinese)

［6］ 肖峻，王成山，周敏.基于区间层次分析法的城市电网规划综合评判决策［J］.中国电机工程学报，2004，24(4):50－57.XIAO Jun，WANG Cheng－shan，ZHOU Min.An IAHP－based madm method in urban power system planning［J］.Proceedings of the Chinese Society for Electrical Engineering，2004:24(4):50－57.(in Chinese)

［7］ 邹礼瑞，毛兵宇.动态模糊层次分析法在不同运输方式综合评价研究中的应用［J］.系统工程理论方法应用，1993，2(3):50－55.ZOU Li－rui，MAO Bing－yu.An application of dynamic fuzzy analytical hierarchy process to the comprehensive evaluation of different transportation means［J］.System Engineering－Theory Methodology Application，1993，2(3):50－55.(in Chinese)

［8］ 孙才志，林学钰，王金生.水资源系统模糊优化调度中的动态AHP 及应用［J］.系统工程学报，2002，17(6):551－555.SUN Cai－zhi，LIN Xue－yu，WANG Jin－sheng.Dynamic AHP in water resources system fuzzy optimal scheduling and its application［J］.Journal of Systems Engineering，2002，17(6):551－555.(in Chinese)

［9］ 钱钢，冯向前，徐泽水.区间数互补判断矩阵的一致性［J］.控制与决策，2009，24(5):723－728.QIAN Gang，FENG Xiang－qian，XU Ze－shui.Consistency of interval complementary comparison matrix［J］.Control and Decision，2009，24(5):723－728.(in Chinese)

［10］ 徐泽水.三角模糊数互补判断矩阵的一种排序方法［J］.模糊系统与数学，2002，16(1):47－50.XU Ze－shui.A method for priorities of triangular fuzzy number complementary judegment matrices［J］.Fuzzy Systems and Mathematics，2002，16(1):47－50.(in Chinese)

［11］ 孙才志，姜俊超，孙培立，等.动态模糊规划模型的构建及应用［J］.数学的实践与认识，2006，36(5):118－127.SUN Cai－zhi，JIANG Jun－chao，SUN Pei－li，et al.Construction of dynamic fuzzy programming model and its application［J］.Mathematics in Practice and Theory，2006，36(5):118－127.(in Chinese)

［12］ 吴瑕，周焰，杨龙坡，等.模糊动态AHP 导弹识别算法［J］.光电工程，2009，36(9):6－11.WU Xia，ZHOU Yan，YANG Long－po，et al.Missile recognition based on the fuzzy dynamic AHP algorithm［J］.Opto－Electronic Engineering，2009，36(9):6－11.(in Chinese)

［13］ Van Laarhoven P J M，Pedrycz W.A fuzzy extension of satty’s priority theory［J］.Fuzzy Set s and Systems，1983，11(1):229－241.

［14］ 徐泽水.对方案有偏好的三角模糊数型多属性决策方法研究［J］.系统工程与电子技术，2002，24(8):9－13.XU Ze－shui.Study on method for triangular fuzzy number based multi－attribute decision making with preference information on alternatives［J］.Systems Engineering and Electronics，2002，24(8):9－13.(in Chinese)

［15］ 龚艳冰，陈森发.三角模糊数互补判断矩阵的一种排序方法［J］.模糊系统与数学，2008，22(1):127－131.GONG Yan－bing，CHEN Sen－fa.A method for priority of triangular fuzzy number complementary judgment matrix［J］.Fuzzy Systems and Mathematics，2008，22(1):127－131.(in Chinese)

［16］ 林焰，郝聚民，纪卓尚，等.隔离小生境遗传算法研究［J］.系统工程学报，2000，15(1):86－91.LIN Yan，HAO Ju－min，JI Zhuo－shang，et al.A study of genetic algorithm based on isolation niche technique［J］.Journal of System Engineering，2000，15(1):86－91.(in Chinese)