不确定健康评估下基于状态维修的效果研究

杨述明，邱静，刘冠军，徐玉国，王超

(国防科学技术大学机电工程与自动化学院 装备综合保障技术重点实验室，湖南 长沙410073)

随着武器装备功能、结构及其技术复杂性的增加，对其维护与保障工作提出了新的要求。装备的维修保障模式在总体上将逐步由定期维修、事后维修向基于状态维修(CBM)发展［1－3］。CBM 以装备的健康状态为依据触发维修行为，因此健康评估的准确性将直接影响CBM 决策的正确性［4－6］。目前大量研究集中在健康评估技术和CBM 技术本身［7－9］，很少关心健康评估效果对装备CBM 效果的影响。事实上，由于装备健康状态退化过程的随机性和动态性以及健康评估模型和算法本身的不确定性，健康评估结果存在不确定性［］。不确定健康评估直接影响CBM 行为决策，导致维修过剩或维修不足，从而最终影响装备的战备完好性。针对该问题，本文首先定义了不确定健康评估、CBM 效果的定量评价指标，然后基于Markov 状态转移过程和稳态平衡原理建立两者之间的关联关系，最后用两个装备实例验证了所提方法的可行性和合理性。

1 CBM 效果、不确定健康评估定量描述

1.1 装备健康状态描述

装备健康状态的描述存在很多形式，主要包括定性描述和定量描述。定性描述一般把装备健康状态退化过程划分成离散的状态，如三状态描述为正常、性能下降和功能失效［3］，五状态描述为健康、比较健康、亚健康、临界健康、完全失效(故障)［10］。定量描述引入健康指标(HI)概念［11］，它把装备健康水平映射成［0，1］之间的值。当装备处于完全健康时，HI =1;当装备完全失效时，HI =0;当装备处于二者之间时，0 ＜HI ＜1.本文把装备的健康状态退化过程离散成n+1 个状态，即健康状态空间为HS={1，2，…，n +1}，状态1 表示完全健康，状态n +1表示完全失效(故障)，状态{2，3，…，n}表示装备健康逐渐退化状态。

1.2 CBM 效果定量描述

CBM 通过机内或外置测试获取装备的状态信息，评估装备健康状态以决定维修时间和维修方式，从而有效提高装备的战备完好性和任务持续能力。从数学上讲，稳态可用度是装备工作时间趋于无穷大时装备的可用程度［12］，反映了装备长期使用过程中的战备完好性与任务持续能力。CBM 的突出优越性就在于使得装备的可用度得到了提高，因此，可以使用稳态可用度来刻画装备CBM 效果。

本文在装备健康状态退化过程建模和控制限维修策略(CLMP)基础上给出稳态可用度的解析表达。装备健康状态退化过程具有连续性、随机性、递增性和不可逆性等特点，一般采用连续的gamma 过程建模［13］。但若忽略装备健康状态退化间的微小差异，可以用连续时间马尔可夫链(CTMC)进行建模［14］。

设装备任意时间t 的健康状态为随机变量X(t)，则满足马氏性的随机过程{X(t)，t≥0}是定义在HS上的CTMC.CLMP 指当装备健康状态处于［1，k－1］时，不进行任何维修;当装备健康状态处于［k，n］时，采用CBM;当装备健康状态为n +1 时，装备完全失效(故障)，采用修复性维修或更换，k 和n 称为CBM 控制限和修复性维修控制限。整个过程如图1所示。

图1 装备健康状态退化过程及CLMPFig.1 Equipment health state degradation process and CLMP

设装备在各个健康状态处于可工作的概率为pi，0，1≤i≤n，则装备的稳态可用度A 可表示为

1.3 健康评估的不确定性描述

由于状态信息输入、评估算法和评估模型的不确定性导致健康评估存在误差，使得装备“该修而不修，不该修而修”。本文结合CLMP 引入正确评估率、欠评估率和过评估率来描述装备健康评估的不确定性。设任意时刻t 装备的健康状态真值为随机变量X0(t)，评估值为X(t)，定义如下

正确评估率

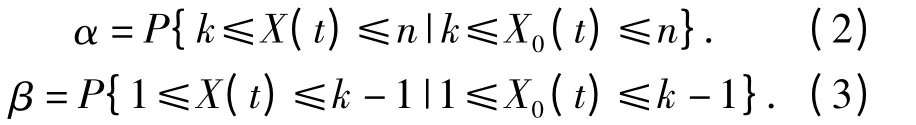
欠评估率

过评估率

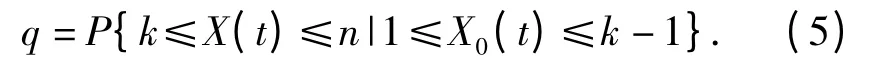
显然

从上面定义可以看出:正确评估率反映了装备正确决策“维修”和“不修”的可能性，而欠评估率和过评估率反映了装备“该修而不修”和“不该修而修”的错误决策可能性。

2 不确定健康评估下的CBM 效果

2.1 模型假设

1)装备健康状态转移率λ、健康状态评估频率λH和评估时间1/μH均服从指数分布;

2)装备存在三种形式的维修:把在区间［1，k－1］的健康状态过评估为区间［k，n］之间的状态导致的CBM、把在区间［k，n］的健康状态正确评估为［k，n］之间的状态导致的CBM 和装备完全故障时的修复性维修，维修时间分别为1/μP1、1/μP2和1/μF，均服从指数分布，且相互独立;

3)通过CBM 和修复性维修后的装备返回最初的工作状态，即修复如新。

2.2 状态及概率定义

S(i，0):装备在第i 个健康状态退化阶段处于工作状态，pi，0=P{S(i，0)}，1≤i≤n;

S(i，1):装备在第i 个健康状态退化阶段处于评估状态，pi，1=P{S(i，1)}，1≤i≤n;

S(F):装备健康处于完全失效状态，pF=P{S(F)};

S(p，2):装备健康状态不准确评估(过评估)下的CBM 状态，pp，2=P{S(p，2)};

S(p，3):装备健康状态正确评估下的CBM 状态，pp，3=P{S(p，3)};

装备在一个运行周期内，状态之间以一定的概率相互转移，状态及其转移概率构成马尔可夫链，如图2所示。

图2 状态转移图Fig.2 State transfer graph

2.3 关联模型建立

根据马氏过程平稳状态下的统计平衡原理，即流入某个状态的平均传递率等于流出该状态的平均传递率，则有如下方程组

对于状态S(1，0)

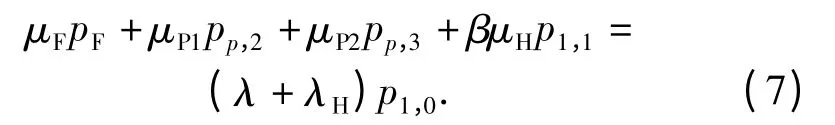
对于状态S(2，0)～S(k－1，0)

对于状态S(k，0)～S(n，0)

对于状态S(F)

对于状态S(1，1)～S(k－1，1)

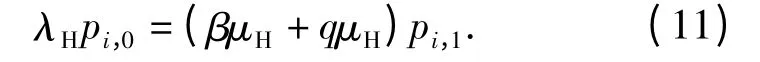
对于状态S(k，1)～S(n，1)

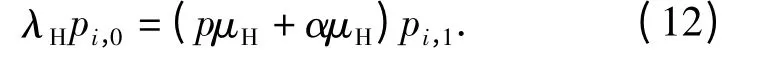
对于状态S(p，2)

对于状态S(p，3)

一共有2n+3 个状态，状态方程有2n+3 个，而装备在平稳状态下所有状态概率之和为1，即

因此，可以求出装备在各个健康状态处于可工作的概率pi，0，1≤i≤n，而pi，0是α 和q 的函数，再根据公式(1)可以得到CBM 效果(稳态可用度)与不确定健康评估(正确评估率α、过评估率q)之间的关联关系

3 案例验证

本文通过舰船发动机［15］和某型装备来说明健康评估的不确定性对装备稳态可用度的影响。

案例1:某舰船发动机的健康状态退化过程离散为7 个状态，相邻两个健康状态之间的转移率相同，设为λ.当发动机健康状态处于区间［1，4］时，不采取维修措施;当发动机健康状态处于区间［5，7］时，采用CBM;当发动机健康状态超过7 时，进行修复性维修。已知该发动机的平均寿命周期为1 000 h，平均健康状态评估时间为2 h，由于健康状态过评估导致的平均CBM 时间为10 h，正确的CBM 平均时间为20 h，修复性维修时间为100 h.由此可得:λ=0.007，λH=0.01，n=7，k=5，T=1 000，μH=0.5，μP，1=0.1，μP，2=0.05，μF=0.01.

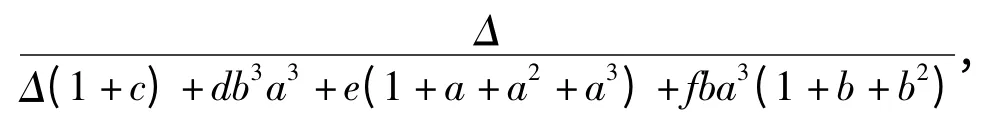
其中Δ=1 +a+a2+a3+ba3+b2a3+b3a3.

采用计算机仿真的方法得到发动机稳态可用度A 与正确评估率α 和过评估率q 的关系如图3所示。

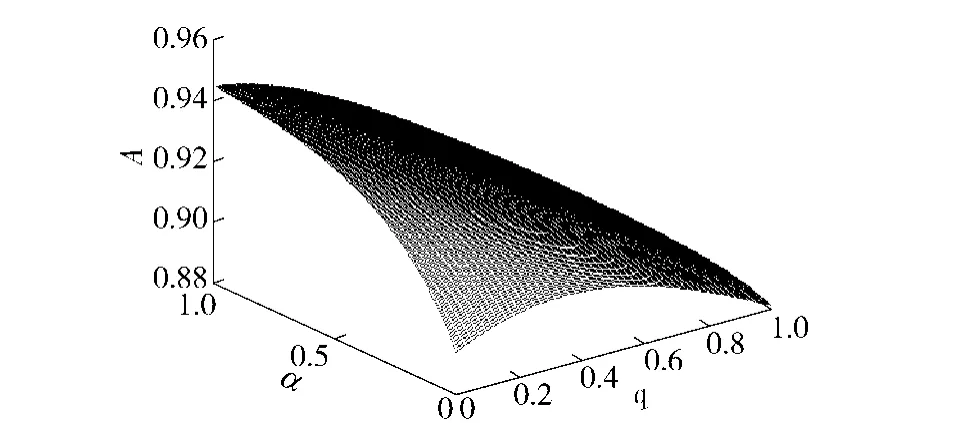
图3 舰船发动机稳态可用度与正确评估率和过评估率间的关联关系Fig.3 Dependency between steady－ state availability and accurate evaluation probability and excessive evaluation probability

物理解释:从舰船发动机的维修性参数可以看出，修复性维修时间占寿命周期的比例很大，而CBM 时间占用寿命周期的比例很小，即修复性维修时间比CBM 时间造成的停机时间更长，因此，该发动机可以采用CBM 提高稳态可用度。健康评估越准确，即α 越大，发动机进行正确CBM 的概率就越大，稳态可用度也就越大;当健康评估不准确时，即q 越大时，把在正常工作状态的发动机也进行了CBM，从而使得可用度降低。当α=1，q=0 时，可用度最大，为0.944 7.

案例2:某型装备的一个寿命周期划分为7 个健康状态，相邻两个状态之间的转移率相同，设为λ.当健康状态处于区间［1，4］时，不采取维修措施;当健康状态处于区间［5，7］时，采用CBM;当健康状态超过7 时，进行修复性维修。已知该装备平均寿命周期为1 500 h，平均健康状态评估时间为0.3 h，由于健康状态过评估导致的平均CBM 时间为0.6 h，正确的CBM 平均时间为1.2 h，修复性维修时间为2 h.由此可得:λ =0.005，λH=0.01，n =7，k=5，T=1 500，μH=1/0.3，μP，1=1/0.6，μP，2=1/1.2，μF=0.5.

通过计算机仿真的方法得到该装备稳态可用度A 与正确评估率α 和过评估率q 的关系如图4所示。

图4 某型装备稳态可用度与正确评估率和过评估率间的关联关系Fig.4 Dependency between steady－ state availability and accurate evaluation probability and excessive evaluation probability

物理解释:某型装备在设计时并行开展了维修性、测试性和可靠性设计，使得其维修性和测试性水平大大提高，表现在修复性维修时间相对于寿命周期的比例很小，并且修复性维修时间和CBM 时间相差不大。在这种情况下，一般就让装备运行到寿命周期末，然后采用修复性维修。也就是说，CBM 对提高稳态可用度不大，因此正确评估率对可用度影响也不大;但是过评估率会把本来不需要进行任何维修的状态评估为CBM 状态，从而使得稳态可用度降低。当α=1，q=0 时，可用度最大，为0.995 6.

4 结论

1)在装备健康状态退化模型和控制限维修策略的基础上提出了用于定量描述不确定健康评估效果和CBM 效果的指标;

2)利用CTMC 建立了装备退化状态、维修状态转移模型，并基于马氏过程的统计平衡原理建立了稳态可用度与正确评估率和过评估率之间的关联关系;

3)通过两个案例验证了所建模型的合理性和可行性。

References)

［1］ Bengtsson M，Olsson E，Funk P，et al.Technical design of condition based maintenance system－A case study using sound analysis and case－based reasoning［C］∥Maintenance and Reliability Conference，Proceedings of the 8th congress，Knoxville:2004.

［2］ 马飒飒，陈国顺，方形桥.复杂装备故障预测与健康管理系统初探［J］.计算机测量与控制，2010，18(1):1－4.MA Sa－sa，CHEN Guo－shun，FANG Xing－qiao.Research on prognostics and health management system of complex equipment［J］.Computer Measurement ＆ Control，2010，18(1):1－4.(in Chinese)

［3］ 梁旭，李行善，张磊，等.支持视情维修的故障预测技术研究［J］.测控技术，2007，26(6):5－8.LIANG Xu，LI Xing－shan，ZHANG Lei，et al.Survey of fault prognostics supporting condition based maintenance［J］.Measurement ＆Control Technology，2007，26(6):5－8.(in Chinese)

［4］ 孙博，康锐，谢劲松.故障预测与健康管理系统研究和应用现状综述［J］.系统工程与电子技术，2007，29(10):1762－1767.SUN Bo，KANG Rui，XIE Jin－song.Research and application of the prognostic and health management system［J］.Systems Engineering and Electronics，2007，29(10):1762－1767.(in Chinese)

［5］ Volponi A.Development of an information fusion system for engine diagnostics and health management ［R］.NASA/TM－2004－212924.

［6］ 吴波，贾希胜，夏良华.基于灰色聚类和模糊综合评判的装备－装备群健康状态评估［J］.军械工程学院学报，2009，21(5):1－5.WU Bo，JIA XI－sheng，XIA Liang－hua.Health assessment of equipment－equipment cluster based on grey clustering and fuzzy synthetic evaluation［J］.Journal of Ordnance engineering college，2009，21(5):1－5.(in Chinese)

［7］ 张亮，张凤鸣，杜纯.复杂装备健康状态评估的粗燥核距离度量方法［J］.计算机工程与设计，2009，30(18):4269－4271.ZHANG Liang，ZHANG Feng－ming，DU Chun.Research on health condition assessment method for complex equipment based on rough set and kernel space distance metric［J］.Computer Engineering andDesign，2009，30(18):4269－4271.(in Chinese)

［8］ Lin D M，Murray Wiseman，Dragan Banjevic，et al.An approach to signal processing and condition－based maintenance for gearboxes subject to tooth failure［J］.Mechanical Systems and Signal Processing，2004，18(5):993－1007.

［9］ Kamran S，Hamid B，Arash B，et al.A new condition based maintenance model with random improvements on the system after maintenance actions:optimizing by monte carlo simulation［J］.World Journal of modeling and simulation，2008，4(3):230－236.

［10］ 王俨剀，廖明夫.航空发动机健康等级综合评价方法［J］.航空动力学报，2008，23(5):939－945.WANG Yan－kai，LIAO Ming－fu.Study on grading of health condition of aerospace propulsion system［J］.Journal of Aerospace Power，2008，23(5):939－945.(in Chinese)

［11］ Jaw L C，Friend R.ICEMS:A platform for advanced conditionbased health management［C］∥Proceedings of IEEE Aerospace Conference on Aerospace，Bigsky:MT，USA，2001:2909－2914.

［12］ Raje D V，Olaniya R S，Wakhare P D，et al.Availability assessment of a two－unit stand－by pumping system［J］.Reliability Engineering and System Safety，2000，68(3):269－274.

［13］ Kallen M J，van Noortwijk J M.Optimal maintenance decisions under imperfect inspection［J］.Reliability Engineering and System Safety，2005，90(2－3):177－185.

［14］ Tseng S T，Peng C Y.Stochasticdiffusion modeling of degradation data［J］.Journal of Data Science，2007，5(3):315－333.

［15］ Cassady C R，Iyoob I M，Schneider，K Pohl E A.A generic model of equipment availability under imperfect maintenance［J］.IEEE Transactions on Reliability，2005，54(4):564－571.