面向网络实时风险预测的马尔可夫时变模型

刘刚，李千目，刘凤玉，张宏

(南京理工大学 计算机科学与技术学院，江苏 南京210094)

0 引言

随着网络技术的广泛应用，其多样性、开放性和互联性的特点，给网络带来了巨大的风险影响，使得网络容易受到各种攻击的威胁。如果能够实时准确的预测网络中的安全风险概率，则对提高网络安全性至关重要。

为了能够有效地预测网络安全风险，近年来，研究人员纷纷对风险预测进行了研究。文献［1］提出了一种基于免疫的网络安全风险检测模型，通过检测网络虚拟抗体浓度，在网络系统面临攻击时对其进行实时风险评估，但该方法仅检测出风险的大小，并未能预测出未来的风险发生概率。文献［2］利用BP 神经网络，结合平均向量相似系数来预测信息交互风险概率，但由于神经网络结构的选择缺乏理论指导，而且对大样本数据学习速度慢，故该预测模型缺乏实时性。文献［3］基于灰色理论提出了一种P2P 网络架构下的风险评估预测方法，但该方法存在明显的系统误差，使得预测的准确性不高。

本文基于马尔可夫模型，摒弃马尔可夫预测对系统状态转移概率矩阵不随时间变化的假设，提出了一种新的网络安全攻击实时风险概率预测模型。

1 马尔可夫时变预测模型

定义:马尔可夫链是随机变量X1，X2，X3…的一个数列。随机变量的范围，被称为“状态空间”。如果Xt+k对于过去状态的条件概率分布仅是Xt的一个函数，则

这里Xt+k=it+k为t+k 时刻过程处于it+k状态。

上面这个恒等式可以被看作是马尔可夫性质。即t+k 时刻系统状态Xt+k=it+k的概率分布只与t时刻的状态有关，与t 时刻以前的状态无关。

定义:马尔可夫链模型可表示为(S，P，π)［4］，其中，

1)S 是系统所有可能的状态所组成的非空的状态集，即系统的状态空间。如网络的状态空间为S={1，2，…，N}其中1 表示始态，N 表示终态。

2)P =［pij(t，t+k)］n×n是系统的状态转移概率矩阵，pij(t，t+k)=P{Xt+k=j|Xt=i}，i，j∈S 表示系统在时刻t 处于状态i，经过k 步状态转移处于状态j 的概率。由于链在时刻t 从任何一个状态出发，到另一个时刻t+k，必然转移到诸状态中的某一个，所以对于任意i∈S，则有

3)π=［π1π2… πn］是系统的初始概率分布，πi是系统的初始时刻处于状态i 的概率，满足

对于pij(t，t+k)=P{Xt+k=j|Xt=i}，i，j∈S，当k=1 时，称pij(t，t+1)=pij(1)为时刻t 的一步状态转移概率，记P 为一步状态转移概率矩阵。

定理:设{Xt，t=1，2…n}是一马尔可夫链，则对任意的时刻u，v，有

证明:对于固定的时刻s，u，v 和状态i，j，k，由条件概率定义和乘法定理，有

又由于事件组“Xs+u=k”，k =1，2，…n 构成一个划分，故有

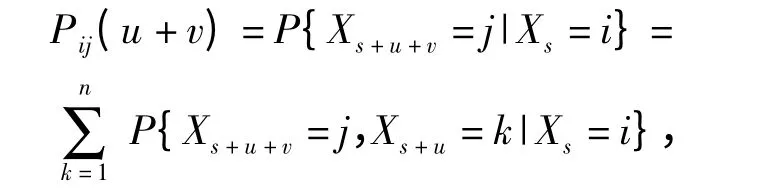
将(2)式代入上式，定理得证。

(1)式写成矩阵形式

推论:k 步转移概率矩阵是一步转移概率矩阵的k 次方。即Pk=P·Pk－1=Pk

证明:利用(3)式，令u =1，v =k－1，得递推关系

记行向量π(k)=［π1(k)，π2(k)，…，πn(k)］，其中，πj(k)表示事件在初始(k =0)状态为已知的条件下，经过k 次状态转移后，在第k 个时刻处于状态j 的概率。且

根据马尔可夫过程的无后效性、贝叶斯条件概率公式及推论，有

式中:π(0)=［π1(0)，π2(0)，…，πn(0)］为初始状态概率向量。Pi(i =1，2，…，k)表示系统的i 步状态转移概率矩阵。

从上述推理可以看出，传统的马尔可夫预测模型是基于假设系统状态转移概率矩阵是不随时间变化的。然而在许多实际问题中，特别是在网络攻击环境中，状态的转移概率，是不断发生变化的，因此本文根据系统状态来实时更新状态转移概率矩阵。

由于状态的转移概率是不断发生变化的，则由(2)式可得

式中，P'仅为一个符号，表示t+1 时刻对t 时刻状态转移概率矩阵的更新。(6)式中的P'并不相等。

由以上分析可知，如果某一事件在第0 个时刻的初始状态已知，即π(0)已知，则利用递推公式(6)，就可以求得它经过k 次状态转移后，在第k 个时刻处于各种可能的状态的概率，即π(k)，从而就得到该事件在第k 个时刻的状态概率预测。因此，如何确定状态转移概率矩阵P'是预测的关键。

2 基于Markov 时变预测模型的实时风险概率预测

网络攻击一般由信息收集阶段、攻击进行阶段、攻击完成阶段三部分构成，根据攻击的不同阶段，将网络风险状态划分为:无风险状态L0(即网络处于正常状态)、轻微风险状态L1(网络处于被探测状态)、较严重风险状态L2(网络处于被攻击状态)和严重风险状态L3(网络已被攻陷)。这些状态构成了马尔可夫时变预测模型中的状态空间，即S ={L0，L1，L2，L3}，则网络的风险状态转移如图1所示。

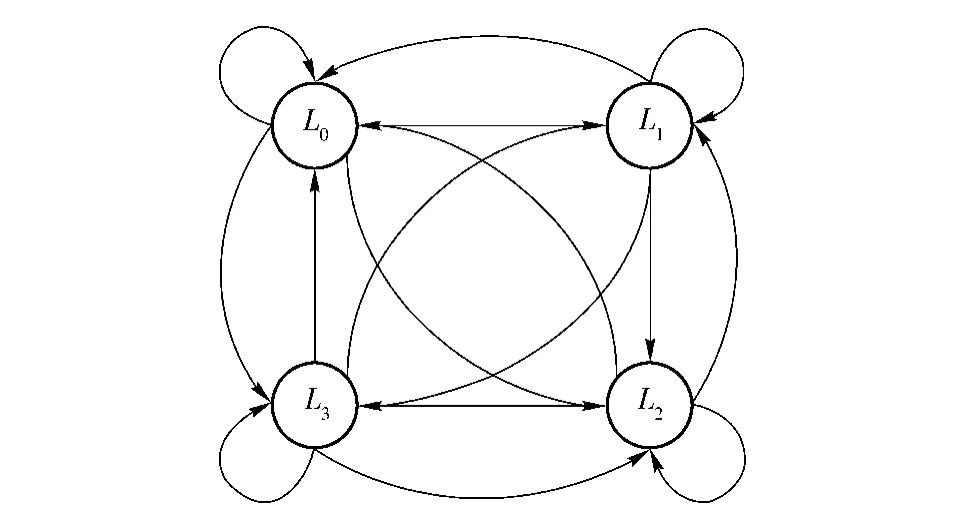
图1 网络风险状态转移Fig.1 Risk state transition of network

由此可确定网络风险状态转移概率矩阵为

计算状态转移概率矩阵P1，就是计算从每个状态转移到其他任何一个状态的状态转移概率。状态转移概率的计算一般采用频率近似概率的思想进行计算。

式中:nij为从状态i 出发，转移到状态j 的样本数。

更新状态转移概率矩阵P'实时迭代的算法下:

第1步:根据以往历史样本数据，利用(7)式、(8)式计算出初始的状态转移概率矩阵;

第2步:对历史样本数据进行初始化。输入数据对象集X，输入指定簇数目N，并在X 中随机选取N 个对象作为初始簇中心。设定迭代终止条件，比如最大循环次数或者簇中心收敛误差容限;

第3步:进行迭代处理。根据相似度准则将数据对象分配到最接近的簇中心，从而形成一簇。初始化隶属度矩阵。以每一簇的平均向量作为新的簇中心，重新分配数据对象;

第4步:反复执行第3 步直至满足终止条件;

第5步:当新样本到达时，计算内聚度，得到新样本所属网络风险状态簇别。结合上一个样本的风险状态簇别，统计风险状态转移次数。然后回到第1 步重新计算状态转移概率矩阵，来更新。

内聚度计算步骤如下:

第1步:选取欧式距离作为簇划分标准。将新样本记录看作一个n 维向量，任意两个n 维向量i，j的距离可以利用欧式距离来计算，设d(i，j)表示簇G 中任意两个向量间的距离，即

内聚值越大，簇内元素越相似。之后根据状态转移概率矩阵的计算方法，可得到新的状态转移概率矩阵。在初始状态概率已知的条件下，利用(6)式，即得出未来某时刻网络的各个安全风险状态概率值。

3 仿真试验

为了验证实时风险概率预测的马尔可夫时变模型的有效性，本文利用KDD CUP 1999 数据集［］来做仿真试验。根据文献［6］对数据集中各攻击的具体描述，根据攻击阶段不同，表1列出了各种攻击阶段对应的风险等级。

表1 攻击分类Tab.1 Attack classification

由于KDD 数据集太过庞大，故在KDD 数据包选取各攻击阶段的一种攻击数据进行实验。本文所选取的攻击组合为nomal、satan、guess_passwd 和rootkit.根据表1对38 种攻击的分类，实验抽取2%的normal 数据(2 192 条记录)、全部satan 数据(1 589条记录)、全部guess_passwd 数据(53 条记录)和全部rootkit 数据(10 条记录)作为实验训练数据。

KDD CUP 1999 数据集中共有41 个定性和定量属性特征，其中有8 个离散属性变量，33 个连续属性变量。由于该数据集中属性太多，增加了分析的复杂性，为了减轻分析的负担，提高风险预测效率，实验中采取主成分分析法，对原有属性进行主成分提取，降低特征向量维数［7］。在保证原始数据信息损失最小的前提下，用较少的属性代替原来较多的属性但依然能反映原有的大部分信息。

实验中除去了全部字符型属性变量和取值全为零的属性变量，对剩下的26 个属性进行特征提取，提取特征值大于1、未经旋转的主成分。表2给出了主成分分析的结果。

从表2可以看出，前6 个主成分的累计贡献率已达到81.437%，这6 个主成分可以基本反映原有属性所具有的信息，这样既减少了变量的个数，降低了20/26 =77%的运算量，又便于问题的全面分析和研究。

主成分分析后，进一步对训练数据分成四个簇用C1，C2，C3，C4来表示，分别代表四种安全风险状态L0、L1、L2和L3.图2给出了簇分布情况，表3给出了簇分析结果，图3给出了簇的分布趋势。

当新样本数据到来时，将新样本数据分别加入到上述4 种簇中，然后根据内聚度的定义，分别计算各簇的内聚度，比较内聚度数值的大小，内聚度数值越大，说明新样本与该簇越相似，故可将新样本数据加入到内聚度最大的簇中。

表2 主成分分析结果Tab.2 The results of principal component analysis

图2 簇分布情况Fig.2 Cluster distribution

表3 簇分析结果Tab.3 The results of cluster analysis

图3 簇分布趋势Fig.3 Cluster distribution trends

对训练样本数据中各状态转移的次数进行统计，即前一时刻状态转移到后一时刻状态的次数，统计结果如表4所示。

表4 状态转移次数统计结果Tab.4 The number of state transition statistics

利用(8)式计算的各个状态的转移概率，得到如下初始风险状态转移概率矩阵

由于起初网络是处于正常状态，故可认为其初始状态概率π(0)={1，0，0，0}。将π(0)与(9)式相乘，可以得到

作为网络当前的状态概率。

实验从kddcup.datat.txt 剩余90%的数据中抽取部分由normal、satan、guess_passwd 和rootkit 构成的样本数据集作为测试样本，分4 组进行测试。

时刻T1输入第一组实验测试样本，其由1 000个normal 样本数据组成;

时刻T2接着输入第二组实验测试样本，由1 000个satan 样本数据组成;

时刻T3接着输入第三组实验测试样本，由50个guess_passwd 样本数据组成;

时刻T4最后输入第四组实验测试样本，由10个rootkit 样本数据组成。

当每一组新的测试样本到来时，先对样本进行簇别划分，然后利用风险状态转移概率矩阵的计算方法，重新计算状态转移概率矩阵。最后利用(6)式预测未来各风险级别的概率。

表5至表8分别给出了第一组、第二组、第三组和第四组测试样本的状态转移次数统计。

表5 第一组测试样本状态转移次数统计结果Tab.5 The number of state transition statistics of the first group of test samples

表6 第二组测试样本状态转移次数统计结果Tab.6 The number of state transition statistics of the second group of test samples

根据状态转移概率矩阵更新算法，可分别得到第一组、第二组、第三组和第四组状态转移概率矩阵:

表7 第三组测试样本状态转移次数统计结果Tab.7 The number of state transition statistics of the third group of test samples

表8 第四组测试样本状态转移次数统计结果Tab.8 The number of state transition statistics of the fourth group of test samples

表9给出了Markov 时变模型预测结果，表10给出了传统Markov 预测结果。

表9 Markov 时变模型预测结果Tab.9 The results of Markov time－varying model prediction

表10 传统Markov 预测结果Tab.10 The results of traditional Markov prediction

从实验结果可以看出，基于马尔可夫时变模型预测出的概率向风险等级高的状态转移的速度更快。从输入的测试数据可以看出，网络在每一时刻的测试数据都是同一类型的数据，故网络在每一时刻的风险状态应依次为L0、L1、L2和L3.由于马尔可夫时变模型状态转移概率矩阵是随着样本的加入实时更新的，每次得到的网络状态概率也会不断更新变化，这就使得对风险的预测更加准确客观。仿真实验表明，应用马尔可夫时变模型在T1时刻，网络处于L0状态的风险概率最高;在T2时刻网络处于L1状态的风险概率最高;在T3时刻网络处于L2状态的风险概率最高;在T4时刻网络处于L3状态的风险概率最高，预测结果与实际的测试样本相吻合。而传统马尔可夫预测由于缺乏实时性，导致预测结果与实际偏差较大，准确性较低。

4 结论

本文提出了一种面向网络实时风险预测的马尔可夫时变模型，与传统的马尔可夫预测模型相比，该模型弥补了传统模型中状态转移概率矩阵不随时间变化的不足，通过实时更新状态转移概率矩阵，使得预测结果更加符合实际，更加客观与准确。并利用DARPA 的入侵检测数据，结合特征提取，对该模型进行了仿真实验，实验结果表明该模型具有很好的可行性和有效性。

References)

［1］ 王益丰，李涛，胡晓勤，等.一种基于人工免疫的网络安全实时风险检测方法［J］.电子学报，2005，33(5):945－949.WANG Yi－Feng，LI Tao，HU Xiao－Qin，et al.A real－time method of risk evaluation based on artificial immune system for network security［J］.Acta Electronica Sinica，2005，33(5):945－949.(in Chinese)

［2］ 刘芳，蔡志平，肖侬，等.基于神经网络的安全风险概率预测模型［J］.计算机科学，2008，35(12):28－33.LIU Fang，CAI Zhi－ping，XIAO Nong，et al.Risk probability estimating model based on neural networks［J］.Computer Science，2008，35(12):28－33.(in Chinese)

［3］ Liu X Y，Fu C，Yang J D，et al.Grey model－enhanced risk assessment and prediction for P2P nodes［C］∥Proceeding FCST’09 Proceedings of the 2009 Fourth International Conference on Frontier of Computer Science and Technology.Washington:IEEE Computer Society，2009.

［4］ 尹清波，张汝波，李雪耀，等.基于线性预测与马尔可夫模型的入侵检测技术研究［J］.计算机学报，2005，28(5):900－907.YIN Qing－bo，ZHANG Ru－bo，LI Xue－yao，et al.Research on technology of intrusion detection based on linear prediction and markov model［J］.Chinese Journal of Computers，2005，28(5):900－907.(in Chinese)

［5］ KDD99.KDD99 cup dataset［DB/OL］.http:∥kdd.ics.uci.edu/databases/kddcup99，1999.

［6］ DARPA.Training data attack description［EB/OL］.http:∥www.ll.mit.edu/mission/communications/ist/corpora/ideval/docs/attacks.html，2008－05－14.

［7］ 吴枫，仲妍，吴泉源.基于增量核主成分分析的数据流在线分类框架［J］.自动化学报，2010，36(4):534－542.WU Feng，ZHONG Yan，WU Quan－yuan.Online classification framework for data stream based on incremental kernel principal component analysis［J］.Acta Automatica Sinica，2010，36(4):534－542.(in Chinese)