少保守性网络化控制系统鲁棒保性能容错控制

李炜，王艳飞

(1.兰州理工大学 电信工程与信息工程学院，甘肃 兰州730050;2.甘肃省工业过程先进控制重点实验室，甘肃 兰州730050)

0 引言

随着计算机与信息技术的迅速发展，网络化控制系统(NCSs)已广泛应用于各个行业中，但通讯网络的引入，却导致了诸如时延、丢包等问题，这不仅会降低系统的性能，甚至会使其失稳［1－2］。此外，NCSs 的规模和功能不仅更加庞大、复杂，不确定和故障诱发因素也更多，因而NCSs 对容错能力的需求也更为迫切。

近年来NCSs 的容错控制已取得了一些初步的成果［3－7］。但现存的NCSs 容错控制结果，性能主要以完整性为主，且保守性相对较大。此外，由于被动容错源于鲁棒控制，其本身也具有较大的保守性。因而从减少结果的保守性出发研究具有一定性能的容错控制问题，无疑对提高NCSs 容错的可行性和满意度具有重要意义。

目前，关于NCSs 的保性能容错问题在国内外研究还有限［8－9］，文献［8］针对具有网络时延的不确定NCSs，针对执行器失效故障得到了使系统具有鲁棒保性能容错的时滞不依赖充分条件。文献［9］考虑传感器连续增益故障，以时滞依赖的方法研究NCSs 的鲁棒保性能容错控制问题。对于小时延系统，尽管文献［9］在一定程度上减少了结果的保守性，但是对时延下界仍以0 处理，而实际工程中NCSs 的数据传输总会产生时延，因此这种不考虑时延下界信息的处理方式仍会给结果带来保守性［10］;此外采用状态单时延模型，较新近提出的状态多时延模型对结果也具有更多保守性［11］。

基于此，本文针对具有参数不确定的线性NCSs，同时考虑时变时延、丢包和的影响，基于状态多时延模型，研究了不确定NCSs 的鲁棒保性能容错控制问题。在执行器或传感器失效故障情形下，通过构造适当的Lyapunov－Krasovskii 泛函，得到了保守性较小的NCSs 鲁棒保性能容错时滞依赖充分条件，并以求解具有LMIs 约束的凸优化问题，给出了最优容错控制器的设计方法。由于新模型中考虑了时延下界，证明中引入了适当的自由权矩阵变量，并且未进行模型转换，也无需进行交叉项放大处理，因而所得结果具有较少保守性。

1 NCSs 的时延分析与系统描述

考虑图1所示的不确定NCSs，假设被控对象的状态空间模型为

式中:x(t)∈Rn为状态向量;u(t)∈Rp是控制输入向量=A+ΔA，=B+ΔB;A，B 为具有适当维数的常实矩阵;ΔA 和ΔB 为具有时变特征的不确定参数矩阵，假设不确定参数矩阵范数有界，并具有如下结构:［ΔA ΔB］=GF(t)［E1E2］.其中G，E1和E2为具有适当维数的常实矩阵;F(t)∈Ri×j为未知时变实值连续矩阵函数，其元素Lebegue 可测，且满足F(t)TF(t)≤I，I 为适当维数单位矩阵。

对网络系统作如下假设:传感器节点采用时钟驱动，控制器节点和零阶保持器节点采用事件驱动。数据采用单包传输，且无时序错乱。

首先由图1可知，采样器到控制器的时延为τsc;控制器到零阶保持器的时延为τca;若采用静态反馈控制，整个闭环系统的时延为τk(τk= τsc+τca)，其中:τm≤τk≤τM，τm和τM分别为时延上、下界。

图1 NCSs 时延模型简化结构图Fig.1 The distribution of the time－delay in the NCSs

若假设所有状态向量可测量，采样周期为常数h，并取采样时刻为t*k，k=1，…，∞，则可得(t*k)=)=［x1(t*k)x2(t*k)… xn(t*k)］T.零阶保持器的更新时刻为tk，k =1，…，∞，则状态反馈控制器可表示为u(tk)=Kx(tk－τk)，考虑零阶保持器的动态属性，则有

式中:K 是控制增益矩阵，tk+1为tk之后下一个时刻零阶保持器的更新时刻。

其次，由于网络拥塞和连接中断，不可避免地会导致数据包丢失。因此假设在区间［tk，tk+1)内丢包数目为δk+1，最大丢包数目为则

由(2)式和(3)式可得

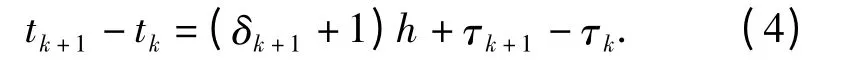
若将(4)式中的(tk－ηk)表示为

则

综合(4)式、(5)式，则有0≤τ(t)≤κ，其中

将(5)式代入(2)式，可得同时考虑时变时延和丢包的状态反馈控制器为

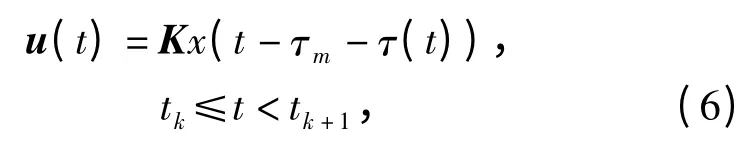
式中:τm为常时延，τ(t)为不可微的时变时延，且满足τm≡C ＜∞，0≤τ(t)≤κ ＜∞.

将(6)式代入(1)式得不确定网络化闭环控制系统为

注1:由于未以采样时刻t*k作为零阶保持器的更新时刻，因此不必考虑零阶保持器与采样器的不同步问题，这更便于实际系统的设计;其次系统模型中引入了时延下界τm，使时变时延τ(t)的上界减少了τm;此外时变时延的变化率未作小于等于1 和可微的限定，更符合网络通讯的实际情形。

2 主要结论

2.1 引理

引理1［12］:给定适当维数的矩阵Q =QT，H，E则

对所有满足FT(t)F(t)≤I 的F(t)都成立的充要条件是存在一正数ε ＞0 使得下式成立

2.2 执行器失效故障时不确定NCSs 鲁棒保性能容错设计

考虑执行器可能发生失效故障的情形，引入开关矩阵L，并把它放在输入矩阵和反馈增益矩阵之间，其形式为L=diag{l1，l2，…，lp}，其中

L∈Ω，Ω 为执行器开关矩阵L 对角元素任取0或1 的各种组合的对角阵集合(L=0 除外)，表示所有可能的执行器失效故障模式的集合。

则不确定网络化闭环故障系统(NCFS)为

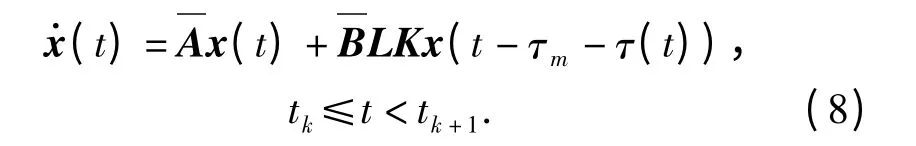
对于系统(8)，定义性能指标为

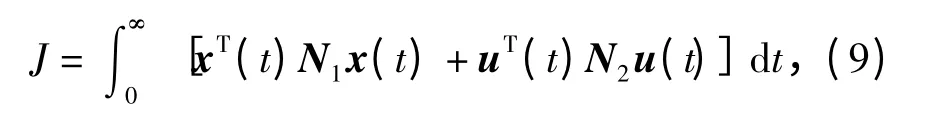
式中，N1，N2为对称正定加权矩阵。

针对执行器失效故障，鲁棒保性能容错控制的设计目标是:寻求状态反馈增益K，使得闭环系统(8)不仅保持鲁棒渐近稳定，且闭环性能指标值满足J≤J.

定理1:对于任意可能的执行器失效故障模式L∈Ω 和可接受的参数不确定性，给定常数ε ＞0，τm，τM和，若存在正定对称矩阵半正定对称矩阵Q 和矩阵满足

则状态反馈(6)式是使不确定NCFS(8)式具有鲁棒保性能的容错控制律，控制器增益可通过K =求得，相应的系统性能指标上界为

式中:

证明:构造Lyapunov－Krasovskii 泛函

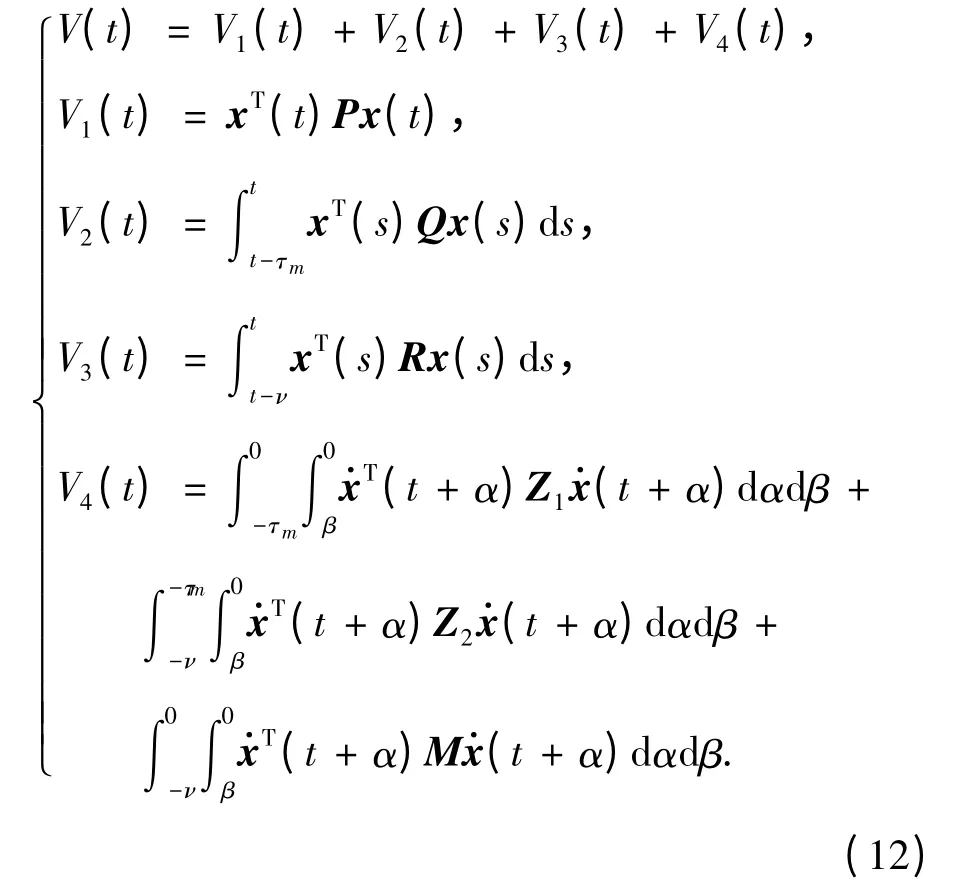
根据Newton－Leibniz 公式，对于任意适当维数的矩阵X，Y，U，V 有θi=0 (i=1，…，4)，

式中:

沿系统(7)的任意轨线，V(t)对时间t 的导数为

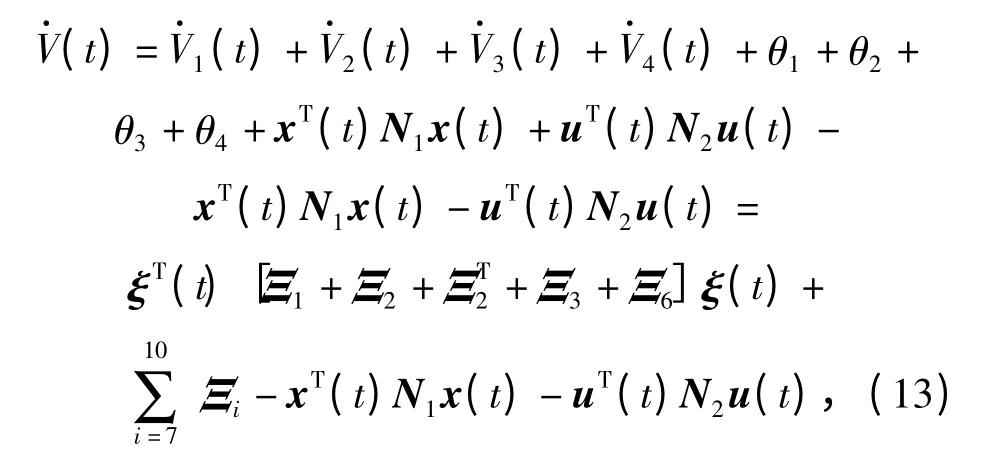
式中:

由前面证明过程可知，若(13)式中的Ξ1+Ξ2+Ξ2T+Ξ3+Ξ6＜0 成立，则有

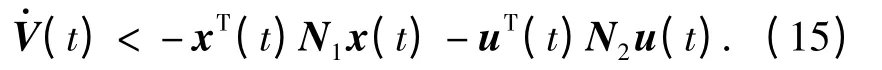
应用Schur 补定理，(15)式等价于(16)式

式中:

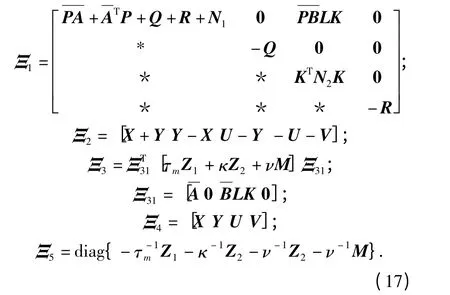
再次应用Schur 补定理，(16)式等价于(18)式

(18)式可转化为下式

其中:Υ=［0 0 K 0］，

若用Γ 表示不含不确定性的Ξ;ΔΓ 表示含不确定性的Ξ;则有Ξ=Γ+ΔΓ，其中

其中

可得

使用引理2，可得

使用Schur 补定理，可得

定义

用J0对(22)式进行合同变换，令便得到(23)式。

式中:

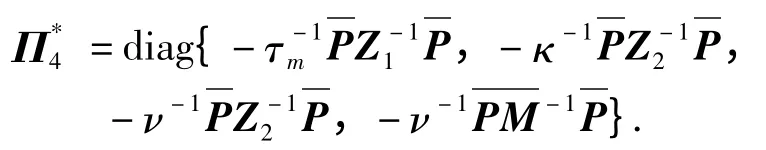
如果以上条件是可行的，则(2)式中的控制器增益矩阵

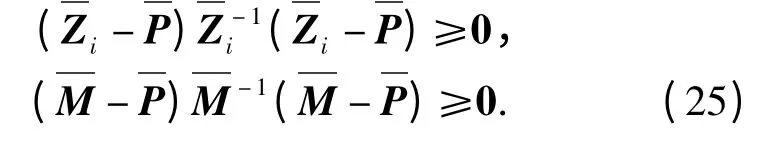
(25)式可转化为

合并(23)式和(26)式便得到(10)式，也即

对(27)式从tk到t∈「tk，tk+1)两边积分，可得

由于V(t)在t∈［t0，∞)内连续，则

在零初始条件下，若t→∞，则可得

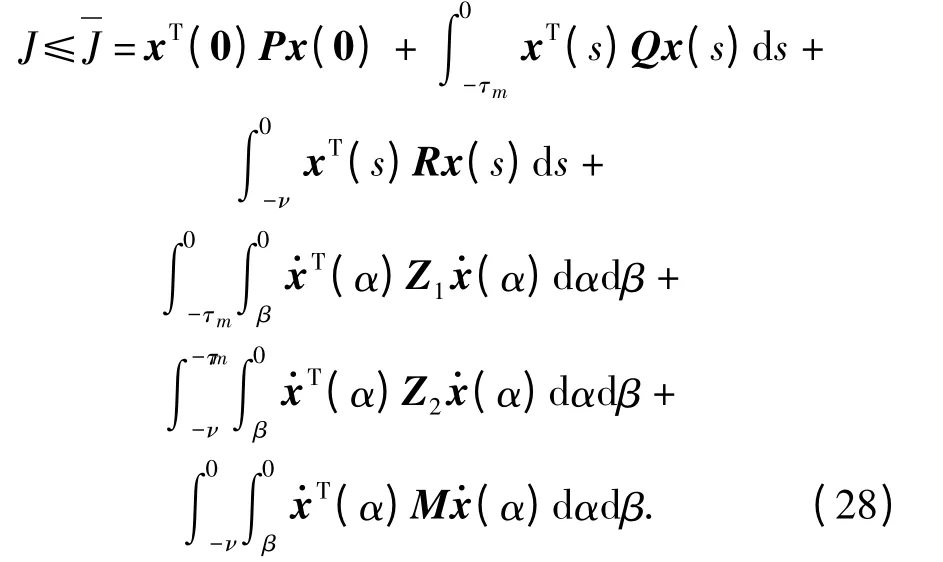
定理证毕。

注2:定理1 中包括了有关时延属性的最大丢包数目δ、时延下界τm、总时延上界ν 以及时变时延上界κ 等所有信息，结果是时滞依赖的。尤其是时延下界τm的引入，可减少保守性［10］。

定理1 得出的结果是一次优鲁棒保性能容错控制器，为了求解出最小的保性能指标上界，定理2 给出了优化方法，进而给出最优鲁棒保性能容错控制器的设计方法。

定理2:对于任意可能的执行器失效故障模式L∈Ω 和可接受的参数不确定性，给定常数ε ＞0，τm，τM和δ，若存在标量δ ＞0，正定对称矩阵半正定对称矩阵和矩阵使得下面的凸优化问题有解

则(24)式为系统(8)的最优鲁棒保性能容错控制器，此时系统的性能指标上界(28)式达到最小。

其中:

证明:因

假设存在标量σ 矩阵W1，W2，W3，W4，W5，考虑到

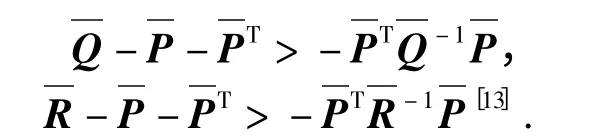
使用Schur 补有

因此有

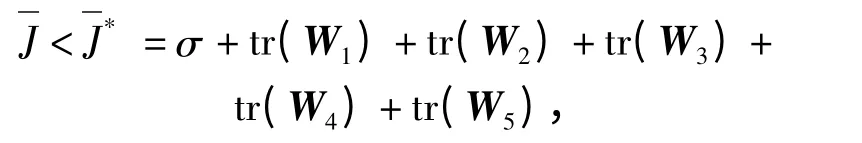
可得到(29)式，定理得证。

2.3 传感器失效故障时不确定NCSs 鲁棒保性能容错设计

考虑传感器可能发生故障的情形，引入开关矩阵F，并把它放在反馈增益矩阵和状态之间，其形式为F =diag{f1，f2，…，fn}其中:

F∈Φ，Φ 为传感器开关矩阵F 对角元素任取0或1 的各种组合的对角阵集合(F =0 除外)，表示所有可能的传感器失效故障模式的集合。

则不确定网络化闭环故障系统(NCFS)为

对于系统(30)，定义目标函数同(9)式。

针对传感器失效故障，鲁棒保性能容错控制目标是:寻求状态反馈增益K，使得闭环系统(30)不仅保持鲁棒渐近稳定，且闭环性能指标值满足J≤

定理3:对于任意可能的传感器失效故障模式F∈Φ 和可接受的参数不确定性，给定常数ε ＞0，τm，τM和，若存在正定对称矩阵半正定对称矩阵和矩阵满足

则状态反馈(6)式是一使不确定NCFS(30)式具有鲁棒保性能的容错控制律，控制器增益可通过(24)式求得，相应的系统性能指标上界为

其中

定理3 的证明类似于定理1，得出的结果仍是一次优鲁棒保性能容错控制器，其最优鲁棒保性能容错控制器的求解方法与(29)式类似，不再赘述。

3 仿真算例

考虑具有参数不确定性的NCSs(1)［5］，其中

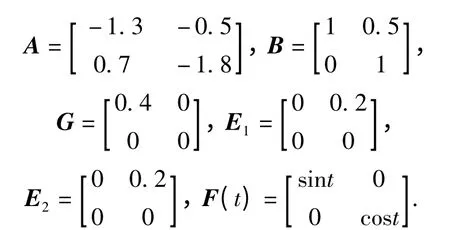
取系统的初始状态为x(0)=［1 1］T.不妨假设采样周期为h=0.1 s.

针对执行器正常及失效故障情形，其中:L0=diag{1，1}，L1=diag{0，1}，L2=diag{1，0}分别表示执行器正常、执行器1，2 发生完全失效故障，引入状态反馈控制律(6)，假设网络参数为τm=0.1s，τM=0.4s 和=2，根据定理2，给定加权矩阵N1=diag{1，1}，N2=diag{1，1}，并取ε=1，利用Matlab 中的LMIs 工具箱，通过求解(10)式，可得到次优鲁棒保性能容错控制器

通过求解(29)式，可得到最优鲁棒保性能容错控制器

相应的闭环系统的最优性能指标为

针对传感器正常及失效故障情形，其中:F0=diag{1，1}，F1=diag{0，1}，F2=diag{1，0}分别表示传感器正常、传感器1，2 发生完全失效故障。仍取ε=1，其它网络参数不变，通过求解优化问题(31)，可得到次优鲁棒保性能容错控制器

通过求解相应的优化问题，可得到最优鲁棒保性能容错控制器

相应的闭环系统的最优性能指标为

采用次优控制器仿真，在执行器或传感器正常与不同故障模式下的NCSs 零输入状态响应曲线如图2所示或如图3所示。

由仿真结果可以看出，在执行器或传感器发生失效故障时，NCFS 不仅稳定，而且具有良好的性能，说明文中所述方法对于具有时变时延和丢包的NCSs 对执行器或传感器发生失效故障时具有鲁棒保性能容错能力。

图2 执行器失效故障情况下系统状态的零输入响应Fig.2 Zero input response of state for actuator failures

图3 传感器失效故障情况下系统状态的零输入响应Fig.3 Zero input response of state for actuator failures

为进一步验证本文所述方法在减少保守性的基础上对性能满意度的提高问题，针对上述被控对象，在传感器失效故障模式下，采用文献［9］的控制器设计方法，利用Matlab 中的LMIs 工具箱进行求解，运行结果是不可行的，也即在相同的时延、丢包情况下，当传感器发生失效故障时，已无法求得使该系统具有保性能容错能力的控制器，从而也昭示出本文所给结果具有更少保守性和较高容错满意度。

4 结论

本文基于状态多时延模型，采用时滞依赖的方法，研究了具有时变时延和丢包的不确定线性NCSs的鲁棒保性能容错控制问题。在执行器或传感器故障情形下，通过构造适当的Lyapunov－Krasovskii 泛函，得到了保守性较小的鲁棒保性能容错时滞依赖充分条件，并以求解LMIs 的方式，给出了最优保性能容错控制器的优化设计方法。由于模型中考虑了时延下界，证明过程中引入适当的自由权矩阵变量，且未进行模型转换和交叉项放大处理，因而使得结果具有较少保守性。仿真示例验证了文中所述方法的有效性。

References)

［1］ Patton R J，Kambhampati C，Casavola A，et al.Fault－tolerance as a key requirement for the control of modern systems［J］.The International Federation of Automatic Control，2006，6(1):26－36.

［2］ Fang H J，Ye H，Zhong M Y.Fault diagnosis of networked control systems［J］.Annual Reviews in Control，2007，31(1):55－68.

［3］ 郑英，方华京.不确定网络控制系统的鲁棒容错控制［J］.西安交通大学学报，2004，38(8):804－807.ZHENG Ying，FANG Hua－jing.Robust fault tolerant control of networked control system with time－varying delays［J］.Journal of Xi an Jiaotong University，2004，38(8):804－ 807.(in Chinese)

［4］ 霍志红，方华京.一类随机时延网络控制系统的容错控制研究［J］.信息与控制，2006，35(5):584－587.HUO Zhi－hong，FANG Hua－jing.Fault－tolerant control of networked control systems with random time－delays［J］.Information and Control，2006，35(5):584－587.(in Chinese)

［5］ 郭一楠，张芹英，巩敦卫，等.一类时变时延网络控制系统的鲁棒容错控制［J］.控制与决策，2008，23(6):689－692.GUO Yi－nan，ZHANG Qin－ying，GONG Dun－wei，et al.Robust fault－tolerant control of networked control systems with time－varying delays［J］.Control and Decision，2008，23(6):689－692.(in Chinese)

［6］ 黎煊，吴晓蓓，王玉龙，等.时变采样周期网络化控制系统的鲁棒容错控制器设计［J］.控制与决策，2009，24(12):1890－1894.LI Xuan，WU Xiao－bei，WANG Yu－long，et al.Robust fault－tolerant controller design ofnetworked control systems under variableperiod sampling［J］.Control and Decision，2009，24(12):1890－1894.(in Chinese)

［7］ 谢晓德，张登峰，黄鹤，等.一类不确定网络控制系统的鲁棒容错控制［J］.信息与控制，2010，39(4):472－478.XIE Xiao－de，ZHANG Deng－feng，HUANG He，et al.Robust fault tolerant control for a class of uncertain networked control systems［J］.Information and Control，2010，39(4):472－478.(in Chinese)

［8］ 李炜，李亚洁.不确定网络化控制系统的保性能鲁棒容错控制［J］.系统仿真学报，2009，21(23):7544－7548.LI Wei，LI Ya－jie.Robust guaranteed cost fault tolerant control for networked control systems with uncertainty［J］.Journal of System Simulation，2009，21(23):7544－7548.(in Chinese)

［9］ 朱灵波，戴冠中，康军，等.具有传感器故障的网络控制系统保性能可靠控制［J］.控制与决策，2009，24(7):1050－1054.ZHU Ling－bo，DAI Guan－zhong，KANG Jun，et al.Guaranteed cost fault－tolerant control of networked control systems with sensor failure［J］.Control and Decision，2009，24(7):1050－1054.(in Chinese)

［10］ Gao H J，Chen T W，James L.A new delay system approach to network－based control［J］.Automatica，2008，44(1):39－52.

［11］ Lam J，Gao H，Wang C.Stability analysis for continuous systems with two additive time－varying delay components［J］.Systems Control Letters，2007，56(1):16－24.

［12］ Petersen I R，Hollot C V.A Riccati equation approach to the stabilization of uncertain linear systems［J］.Automation，1986，22(4):397－411.

［13］ Zhao Y，Zhang C Z，Gao H J.A new approach to guaranteed cost control of T－S fuzzy dynamic systems with interval parameter uncertainties［J］.IEEE Transactions on Systems，Man，and Cybernetics，Part B:Cybernetics，2009，39(6):1516－1527.

［14］ 吴敏，何勇.时滞系统鲁棒控制—自由权矩阵方法［M］.北京:科学出版社，2008.WU Min，HE Yong.Robust control for time－delay systems－freeweighting matrices method［M］.Beijing:Press，Sciences，2008.(in Chinese)