基于复杂网络的装备维修保障协同效能优化设计

徐玉国，邱静，刘冠军

(国防科学技术大学 机电工程与自动化学院 装备综合保障技术重点实验室，湖南 长沙410073)

0 引言

装备复杂性和高技术特性的提升使得装备维修保障工作量显著增加，保障时效性要求大大提高，保障组织指挥更加复杂。适应该需求，装备维修保障系统逐步从传统的三级维修系统结构向网络化结构演变，以网络为中心的装备维修保障系统将成为维修保障系统的发展趋势。如何对网络化结构的复杂装备维修保障系统进行效能分析和优化设计成为急需解决的问题。

在传统的维修保障模式下，维修保障需求平稳且确定，通过固定配置的维修保障能力与维修保障资源便能满足维修需求;比如，Dekker［1］对传统模式下的维修优化问题进行了归纳整理，分析了维修的目标和策略;Wang［2］对劣化系统的维修与换件策略进行了详细的分类，并对单部件与多部件系统的维修策略进行了比较;Jardine［3］等从故障诊断、故障预测的角度对基于状态的维修策略进行分析。同时，维修策略与资源保障策略是相互影响与制约的，维修保障系统中不同节点之间的信息共享对维修与库存也有影响，比如，Wu［4］，Thomas［5］，刘志硕［6］，郝国英［7］等研究了资源供应系统中各个节点的信息共享对系统成本与补给策略的影响;司书宾［8］等研究了基于协同供应的维修备件协同库存控制模型并对其进行了优化求解。上述传统的分析方法，并不完全适用于网络化结构的维修保障系统，有关学者就网络化结构维修保障系统的效能分析和优化设计方法进行了研究。比如，Dodds［9－10］等研究了组织网络的信息交换、鲁棒性与协同演化;Lin［11］等从网络熵与互信息的角度对网络化组织结构的敏捷性进行了分析和探讨;Walter［12］和卜先锦［13］等就军事组织中的信息共享进行了深入的分析;朱涛［14］等从复杂网络的视角研究了指挥控制信息协同模型;Kwon［15］等从Agent 和案例推理的角度对供应与需求不确定环境下的协同机理进行了研究;王小念［16］等研究了网络中心战环境下的信息效能度量方法。

网络化是维修保障系统的天然特性，但是如何从复杂网络的角度研究装备维修保障系统的协同性能尚不多见。本文针对装备维修保障系统的网络化与协同性的特点，引入复杂网络构建装备维修保障系统的网络模型，探讨系统固有的拓扑结构特性与动态演化特性对系统协同性能的影响。同时，基于双层立体加权网络建立了维修保障网络的动态演化模型，以协同效能最大为目标，提出了保障网络最优演化算法，设计了效能最大的保障网络。该模型对网络化分布式的维修保障系统分析具有普适性，为各类装备维修保障系统的协同效能分析提供了一种新的途径。

1 装备维修保障系统的网络特性分析

1.1 装备维修保障网络

装备维修保障系统根据实际的装备维修需求，通过集中式或分布式的信息控制分散于不同地点的各级维修保障资源，实现各类资源的供应、运输、分派、协作与共享，形成一个相互关联、紧密协作的维修保障体系。装备维修保障体系是以装备使用单位、维修单位、库存仓库和备件供应商为节点，以连接这些节点的信息流、物流、指挥控制流为边构成的网络。该网络蕴含一系列子网络，如组织网络、物流供应网络、库存网络、维修网络、运输网络等。如果单纯从网络的连通性考虑，那么组织网络、物流供应网络、维修网络、运输网络可以用无向无权网络模型来描述。如果考虑各维修单位与装备使用单位之间的隶属关系、服务水平等，那么维修网络、物流网络与运输网络就是有向加权网络。

随着现代通信、网络、传感、信息处理、人工智能等技术在装备维修保障领域的应用，以及维修保障活动自身的高度动态性，要求装备维修保障系统必须在网络化与协同性等方面有所改善与提高。

1.2 装备维修保障系统的网络特性分析

1)装备维修保障网络的表示方法［17－21］

将网络中的节点用1，2，…，N 顺序标出，那么N个节点之间关系就组成一个N ×N 矩阵A，其非对角线元素A［u］［v］表示从节点u 到节点v 的边数。当且仅当节点u 与v 之间有连接时，A［u］［v］=1;否则A［u］［v］=0，此即为网络的邻接矩阵。

加权网络可以由集合G =(V，E)描述，包括N个节点组成的集合V，以及带有权重的边集合E;通常可以用加权邻接矩阵W 表示加权网络，其中矩阵元素wij(wij＞0)代表相邻两点间的边权。通常情况下，相似权wij∈［0，∞)，如果wij=0，表示两点之间无连接;而相异权wij∈(0，∞)，wij=∞时相当于两点之间无连接。

2)装备维修保障网络的基本特性［22］

在网络中，节点度数是指连接这个节点的边数。所有节点度数的平均值即为网络的节点平均度D;定义连接任意两个节点的最短路径的边数为这两节点间的距离。所有节点对之间距离的平均值即为网络的特征路径长度APL;某节点的近邻节点之间实际存在的连接边数与其最多可能存在的连接边数的比值定义为该节点的聚类系数，所有节点聚类系数的平均值即为整个网络的聚类系数CC.对于维修保障网络而言，较小的特征路径长度说明网络节点之间的连接更为紧密，其节点间通信、交互与共享的代价更小;另外，越大的聚类系数说明网络节点间的协作效应越明显，同时具有较小的特征路径长度与较大的聚类系数特征的网络称为小世界网络。

3)装备维修保障网络的协同特性［21］

设A 为网络邻接矩阵，设M=diag(dv1，dv2，…，dvN)为网络的度对角矩阵，其中dvi表示节点vi的度，网络的拉普拉斯矩阵可以定义为L =M－A.网络的特征值和特征向量可以更好地描述网络的拓扑结构和动力学特性，从而能够更好地刻画网络的全局特征。例如，网络拉普拉斯矩阵次大特征值与最小特征值的比值(同步协同指数)λ 的大小决定了网络的同步协同能力［23－24］，其中λ 越小，说明该网络的同步协同能力越强。

2 基于复杂网络理论的装备维修保障系统协同效能建模

2.1 装备维修保障网络模型

本文建立双层立体加权网络模型对装备维修保障系统进行建模与分析，首先对装备维修保障网络的基本概念进行定义与说明。

节点vi:表示各级具备维修保障能力的组织实体，集合V={v1，v2，…，vN}为所有维修保障实体的集合。

连接eij:表示节点vi和vj之间的关系，可以体现多个层面的关系，比如，信息流、物流等。

组织网络No(V，Eo):组织网络中的节点表示维修保障体系下的各级实体，组织网络中的连接表示维修保障体系下任意两个节点vi与vj之间的直接隶属(保障与被保障)关系，eo(i，j)∈{0，1}，其中eo(i，j)=1 表示节点vi与vj之间存在直接保障关系，eo(i，j)=0 表示节点vi与vj之间不存在直接保障关系，特别的，eo(i，i)=0.组织网络用邻接矩阵Do表示。

路程网络Nr(V，Er):路程网络中的节点表示维修保障体系下的各个路程节点，路程网络中的连接为物流供应网络中任意两个节点i 与j 之间的最短路程，er(i，j)∈［0，∞)，特别的，er(i，i)=0.路程网络用邻接矩阵用Dl表示。这样，路程网络采用相似权表达，权值越小表示两点间的关系越亲密，距离越小。

维修保障系统网络G:上述节点与双层网络的组合构成了装备维修保障体系的总体网络模型，G={V，No，Nr}.

2.2 维修保障网络协同效能建模

维修保障系统中的节点之间存在十分复杂的交互作用关系，构成复杂的网络结构。传统的维修保障注重单个节点的局部优化，复杂网络环境下的维修保障系统对各个维修保障单元之间的组织协同与信息共享能力有了更高的要求，使得可以在适度增加成本的条件下提升维修保障网络的效能。而网络协同对维修保障效能的影响体现在三个不同的层次:极少协同、适度协同、过度协同［12－13，16，25］，分别如图1所示。

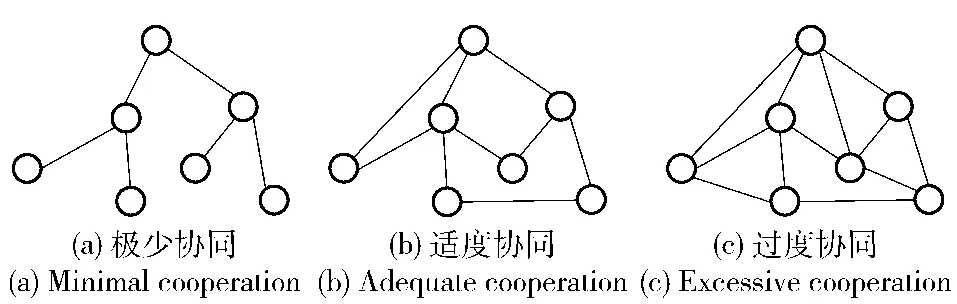
图1 维修保障网络协同效能Fig.1 Cooperation effectiveness of maintenance support network

极少协同:传统的链式维修保障体系结构，维修保障实体之间较少相互协同关系——各个实体节点之间只存在上下级间的保障关系，不存在与其他节点之间的组织协同、信息共享、资源共享等。该维修保障网络的特点是成本低，收益小，效能比较低，与此相应的网络特征是:较大的特征路径长度与同步协同指数，较小的网络成本。

适度协同:在传统的维修保障体系基础上构建了适度有限的信息、资源、维修能力的共享协同关系。该模式下的系统适度增加了成本，获得了最好的收益，效能也是最高的，与此相应的网络特征是:适当的特征路径长度与同步协同指数，较小的网络成本。

过度协同:在适度协同基础上，维修保障体系下的所有节点趋向于全连通的模式，所有的维修保障实体之间均有信息与资源的相互作用，该维修保障网络的特点是过度的协作导致超高的成本，但是收益并没有得到相应的提升，效能也比较低，与此相应的网络特征是:最小的特征路径长度与同步协同指数，最大的网络成本。

综合上述分析可知，装备维修保障网络的特征路径长度越小，维修保障行为中协同共享的代价越小，越有利于系统性能的提升;装备维修保障网络的同步协同指数越小，维修保障行为中协同能力越强;装备维修保障网络的连接越复杂，网络的构建与维护成本越大，对系统来说是需要抑制的负担。构建适当的维修保障网络模型，对改善和提高维修保障系统效能具有重要意义。

3 维修保障网络的动态演化模型

3.1 维修保障网络协同效能优化模型的构建

实际的装备维修保障系统中，考虑到系统的性能与成本，系统应当在适度协同与信息共享的情况下运行，找到影响系统效能的关键环节是提升系统敏捷性、降低维修保障成本、获得最佳系统协同效能的重点。为了设计最优的网络结构使系统达到适度协同的状态，本文力图找到能引导系统趋向于最佳协同效能的演化策略，进而使系统运行于高效状态。

传统的维修保障系统网络化效应极小，随着装备信息化、维修保障行为网络化水平提高，单个节点独立保障或链式保障的策略不能适应新的要求，不能优化保障要素，维修保障节点之间的维修保障能力不能通过共享、协同的形式得以提升。本文构建双层立体加权网络演化模型来分析和设计维修保障网络演化策略(见图2)。

图2 双层立体加权网络演化模型Fig.2 Dynamic evolution model of two－layer weighted network

图2中应用双层立体加权网络模型对装备维修保障网络的演化进行了描述，上层网络节点代表维修保障系统中的维修保障实体，下层网络节点代表路程节点，为了描述与说明问题的方便，省略了与网络特征无关的细节信息。图2(a)表示传统的维修保障网络，由组织网络No，1和路程网络Nr，1组成，图2(b)表示经过演化的维修保障网络，由组织网络No，2和路程网络Nr，2组成，路程网络Nr，1与Nr，2保持一致，而组织网络No，2经由No，1按某种演化策略而得。

3.2 维修保障网络协同效能函数的构建

为了对维修保障网络的协同性能进行分析，分别定义网络协同收益函数B(G)、网络协同成本函数C(G)与网络协同效能函数BC(G)

其中，G 表示装备维修保障系统的网络模型，网络协同效能函数BC(G)越小，说明维修保障网络的协同效能越好。

下面对维修保障网络的协同成本函数C(G)进行分析，考虑其成本结构为:C(G)=f(C0，CL，CK).

其中，构建维修保障网络基础设施的成本包括C0和CL.

C0:每条维修保障链路的基础成本，该值为常数，对于整个维修保障网络而言，网络建设固定成本mC0与网络连接数目呈线性关系，其中m 为网络中连接的数目;

CL:维修保障链路的可变成本，该值与其对应的链路长度成正比，是线性比例系数，Li为第i 条链路长度)。

CK:维修保障复杂性成本，与维修保障网络的复杂性正相关。装备维修保障网络的复杂性k(H)是装备维修保障网络各个实体之间相互协同保障关系数量的函数［16］，即

式中:H 为各个维修保障单元之间平均相互协同共享关系的数量，也即维修保障网络中节点的平均度数。参数a 和b 是可变系数，确定了最小影响的区域和迅速增加影响的区域［16］。k(H)与H 正相关，随着H 的增加而增加。

考虑上述各类成本之间为线性关系，维修保障网络的协同成本函数为

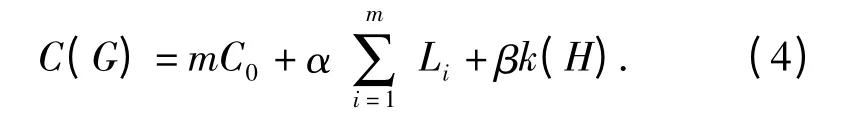
由于维修保障网络中的节点性质与功能的差异性，当由传统的维修保障体系向网络化的维修保障体系演变时，优先建立那些能够用较小的代价获取较大收益的网络连接，使维修保障网络更易于协同与共享，可以获得更好的维修保障效能。

4 维修保障网络协同演化算法

传统的装备维修保障系统中的网络化因素较少，也很少考虑其网络效能，对于以网络为中心的维修保障体系而言，在其网络拓扑的基础上，同时考虑系统网络化收益与网络化成本，并使其趋向于最优效费比，是构建新型维修保障网络协同效能的目标。

维修保障网络的演化策略可以分为:(1)单连接演化策略——每步演化增加一条连接(2)多连接演化策略——每步演化增加多条连接，而策略(2)可以转换为策略(1)的连续多次执行。因此，本文就维修保障网络演化过程中的单连接演化策略下的协同收益、协同成本与协同效能方面进行分析。根据前面分析，维修保障网络的协同收益、协同成本与协同效能均为网络拓扑的函数。维修保障网络协同演化的算法为:

1)在初始网络模型的基础上，确定网络可演化区域。

2)在可演化区域上依次执行策略(1)获得新的网络模型，并计算新模型下的协同收益与成本，获得每一演化区域所对应的网络协同效能，生成网络协同效能向量。

3)在网络协同效能向量中寻找最优值(最小值)所对应的区域即为网络协同演化的最优策略。

4)在整个网络范围内对上述过程进行迭代，确定全局演化策略，计算网络最优演化过程中的协同效能曲线，该曲线的最优值(最小值)即对应整个网络的最优协同演化策略，并辅助设计协同效能最大的保障网络。

维修保障网络协同演化算法的具体流程如图3所示。该算法的复杂度为O(n3)，其中n 表示维修保障网络中节点的数量。

图3 维修保障网络协同演化算法流程图Fig.3 Flowchart of maintenace support network cooperation evolution algorithm

5 应用案例

现以某型装备维修保障系统为例，说明该方法的运用。传统的三级维修保障模式下，装备维修保障系统的结构具有线性、较少协同的特点，将各级维修保障组织均抽象为节点，各组织节点之间的保障关系抽象为连接，维修保障系统的组织网络如图4(a)所示，路程网络如图4(b)所示。

图4 传统装备维修保障系统网络模型Fig.4 Traditional maintenance support system network model

对于装备维修保障体系而言，协同效能主要体现在以下3 个方面:协同实现的难易程度、协同代价的大小、协同效果的优劣。根据复杂网络的定义以及本文定义的效能指标对传统维修保障系统网络结构的整体拓扑特性进行统计计算。其中，关于网络成本方面的参数设置如下:C0=100(元)，α=1(元/m)，β=100 000(元)，a =－7，b =0.7.结果如表1所示。

表1 传统维修保障系统的协同效能指标Tab.1 Cooperation effectiveness metrics for traditional maintenance support network

由表1数据可知，传统的维修保障系统具有较长的特征路径长度与最小的聚类系数，不具备小世界特性与无标度特性。在网络协同效能方面，由于其网络化效应不明显，故其网络协同收益比较差(网络协同收益值较大)，虽然其网络代价最小(网络成本值最小)，但是综合的网络协同效能并非最好(网络协同效能值较大)。这样的维修保障系统不利于系统各节点之间的协作与共享，有待进一步改进。

本文着重讨论装备维修保障网络在信息化条件下如何进行演化以提升其协同效能。而影响维修保障系统网络化协同的因素包括:维修保障单元之间功能的相容性与相似性、维修保障网络的同步能力、维修保障单元之间的平均距离以及在协同演化过程中所增加的成本。

考虑上述影响维修保障系统协同效能的因素，下面应用本文第3、4 节提出的策略对上述模型进行优化处理，并根据复杂网络的定义以及网络协同效能的公式对演化网络的统计特性进行分析;同时为了对比，本文设计了网络随机演化模型，并比较各种演化策略之间的优劣，结果见表2。

表2 维修保障系统的网络效能指标比较Tab.2 Comparison of network effectiveness metrics for maintenance support system

表2中A 表示原始的传统维修保障网络模型，B 表示本文提出的网络演化策略，C 表示一种随机网络演化策略，D 表示另一种随机网络演化策略。此三种维修保障网络演化策略生成的网络均具有较小的特征路径长度与较大的聚类系数，说明三种网络均具备小世界特性。

图5、图6、图7分别详细显示了在三种不同的维修保障网络演化策略下，系统协同收益、系统协同成本与系统协同效能随网络演化过程的变化情况。图5显示不管是哪一种维修保障网络演化策略，在初始阶段，随着网络中演化连接数目的增加，系统协同收益获得了显著提升(系统协同收益函数急剧下降)，而当网络增长到一定规模以后，新增网络连接对系统协同收益的贡献呈现递减趋势，并且其边际效益趋于极小。在三种策略当中，本文提出的优化策略相对于另外两种随机演化策略，能够在维修保障网络演化的初始阶段使系统协同收益尽早达到最优值。

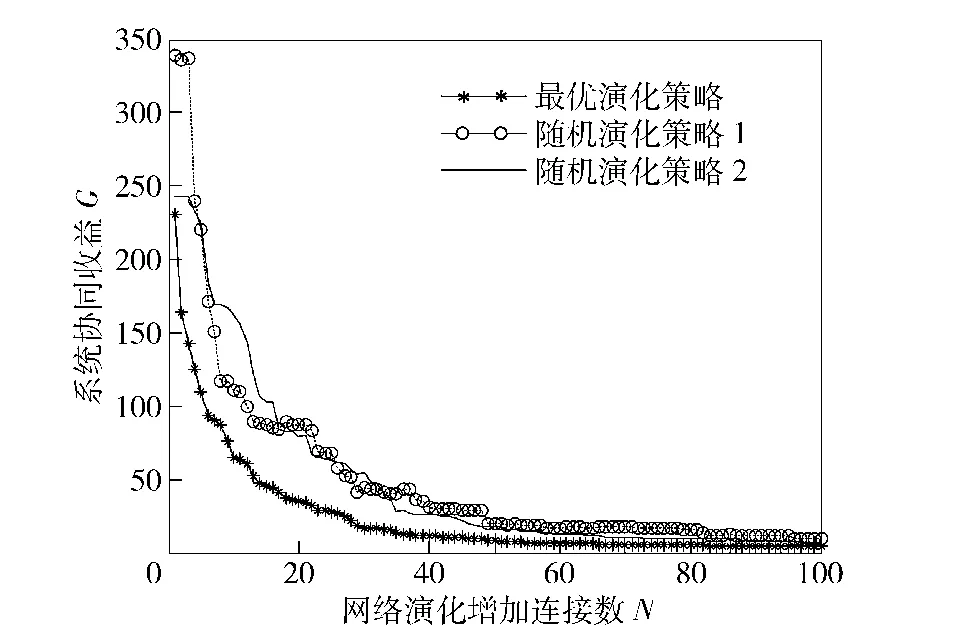
图5 系统协同收益随网络连接增加的变化曲线Fig.5 System cooperation benefit vs.the number of added linkages

图6显示三种维修保障网络演化策略中，系统协同成本随网络演化连接数目增加的变化规律，系统协同成本在经过初始阶段的缓慢上升之后，整个成本曲线的形状与成本函数构成中CK分量的形状大体一致，说明维修保障系统中的指挥复杂性成本对成本函数的影响最为明显。鉴于CK、C0均与网络的平均度相关，而平均度与网络结构无关，只与网络中连接数目的多少相关，也即只与新增连接的数目相关，CL与维修保障系统的路程网络相关，由于该维修保障系统中各节点相对比较集中，各个节点之间的距离相对差距较小，在不同策略的网络演化过程中，CL呈现线性增长趋势，与网络的平均度线性相关，也只与新增连接的数目相关，在三种不同的演化策略下，系统协同成本曲线基本一致。

图6 系统协同成本随网络连接增加的变化曲线Fig.6 System cooperation cost vs.the number of added linkages

图7显示三种维修保障网络演化策略中，系统协同效能随网络演化连接数目增加的变化规律，三条曲线具有相同的趋势，当连接边数增加值为85、87、94 时，三种策略下的维修保障系统的协同效能获得最佳值。在三种不同的策略中，当新增连接数目为56 时，本文提出的最优演化策略的系统成本分别比另外两种随机演化情况降低了5.2%和1.3%，同时系统协同收益分别提高了62.8%和54.5%，系统的整体协同效能分别提高了64.8%和55.1%。说明本文提出的维修保障网络最优演化策略以低成本获得了高收益，优化效果明显。

图7 系统协同效能随网络连接增加的变化曲线Fig.7 System cooperation Effectiveness vs.the number of added linkages

通过本文提出的优化策略，演化后的维修保障网络模型中的组织网络如图8所示。网络的最优演化路径为:A→(12，19)→(16，18)→(7，20)→(16，25)→(7，12)→(12，22)→(15，26)→(1，11)→(15，20)→(11，16)→……

图8 演化后的装备维修保障系统组织网络模型Fig.8 Evolved maintenance support system organizational network model

5 结论

1)全面分析了装备维修保障系统的要素，从组织网络与路程网络两方面进行综合描述，建立了装备维修保障网络的双层立体加权模型。

2)在双层立体加权模型的基础上，建立了网络协同收益、网络协同成本与网络协同效能的数学模型，给出了网络协同效能的评判原则，从本质上辨识出维修保障系统网络的最佳协同效能演化方向。

3)提出了装备维修保障网络的协同演化策略，构建了最佳协同效能演化的求解算法，求得了网络协同演化过程中的最优路径与最优效能值，从而为系统协同效能评估提供了一定的依据，并通过与随机网络演化策略进行比较，彰显了该算法的合理性与有效性。

当然，本文对装备维修保障网络做了很大的程度上的抽象，剔除了在维修保障中的其他许多因素，比如维修需求获取、维修工作调度、维修资源供应等相关环节。在今后的研究工作中，可以逐步结合其他相关因素进行网络模型的扩充与完善，比如，考虑维修保障要素之间的功能关系，考虑维修保障需求与供应特性，使多层维修保障网络能够更加准确地反映装备维修保障系统的特点。同时本文提出的算法的效率也有待进一步提高。

References)

［1］ Dekker R.Applications of maintenance optimization models:a review and analysis［J］.Reliability Engineering and System Safety，1996，51(3):229－240.

［2］ Wang H.A survey of maintenance policies of deteriorating systems［J］.European Journal of Operational Research，2002，139(3):469－489.

［3］ Jardine A K，Lin D，Banjevic D.A review on machinery diagnostics and prognostics implementing condition－based maintenance［J］.Mechanical Systems and Signal Processing，2006，20(7):1483－1510.

［4］ Wu Y N，Cheng T C E.The impact of information sharing in a multiple－echelon supply chain［J］.Int.J.Production Economics，2008，115(1):1－11.

［5］ Thomas K，Panayiotis M，Katerina P.The impact of replenishment parameters and information sharing on the bullwhip effect:A computational study［J］.Computers ＆ Operations Research，2008，35(1):3657－3670.

［6］ 刘志硕，柴跃廷，申金升.信息共享环境下多级复杂供需链系统的库存成本分析［J］.计算机集成制造系统，2007，13(5):984－989.LIU Zhi－shuo，CHAI Yue－ting，SHE Jin－sheng.Inventory cost analysis of complex multi－echelon supply chain with information sharing［J］.Computer Integrated Manufacturing Systems，2007，13(5):984－989.(in Chinese)

［7］ 郝国英，孔造杰，韩海彬.供应链中信息共享对各环节库存的影响研究［J］.系统工程理论与实践，2007，27(9):131－135.HAO Guo－ying，KONG Zao－jie，HAN Hai－bin.The effect of information sharing on inventory in supply Chain［J］.Systems Engineering－Theory ＆ Practice，2007，27(9):131－135.(in Chinese)

［8］ 司书宾，孙树栋，蔡志强，等.基于协同供应的维修备件协同库存控制模型及其算法研究［J］.西北工业大学学报，2007，25(5):636－641.SI Shu－bin，SUN Shu－dong，CAI Zhi－qiang，et al.Cooperative inventory control model and algorithm of spare parts for enhancing equipment’s efficiency［J］.Journal of Northwestern Polytechnical University，2007，25(5):636－641.(in Chinese)

［9］ Dodds P S，Watts D J，Sabel C F.Information exchange and the robustness of organizational networks［J］.PNAS，2003，100(21):12516－12521.

［10］ Hanaki N，Peterhansl A，Dodds P S，et al.Cooperation in evolving social networks［J］.Management Science，2007，53(7):1036－1050.

［11］ Lin Y，Desouza K C，Roy S.Measuring agility of networked organizational structures via network entropy and mutual information［J］.Applied Mathematics and Computation，2010，216(10):2824－2836.

［12］ Walter L，Perry W L，Moffat J.Information sharing among military headquarters:the effects on decision－making ［R］.Santa Monica:RAND Corporation，MG－226，2002:41－55.

［13］ 卜先锦.军事组织协同的建模与分析［M］.北京:国防工业出版社，2009:156－176.BU Xian－jin.Modeling and analysis of military organization cooperation［M］.Beijing:National Defense Industry Press，2009:156－176.(in Chinese)

［14］ 朱涛，常国岑，张水平，等.基于复杂网络的指挥控制信息协同模型研究［J］.系统仿真学报，2008，20(22):6058－6065.ZHU Tao，CHANG Guo－cen，ZHANG Shui－ping，et al.Research on model of command and control information cooperation based on complex networks［J］.Journal of System Simulation，2008，20(22):6058－6065.(in Chinese)

［15］ Kwon O，Im G P，Lee K C.MACE－SCM:A multi－agent and case－based reasoning collaboration mechanism for supply chain management under supply and demand uncertainties［J］.Expert Systems with Applications，2007，33(3):690－705.

［16］ 王小念，皮军明，余巍.一种网络中心战中信息效能度量方法［J］.现代防御技术，2007，35(5):14－18.WANG Xiao－nian，PI Jun－ming，YU Wei.A method of information efficiency evaluation in NCW［J］.Modern Defense Technology，2007，35(5):14－18.(in Chinese)

［17］ Albert R，Barabási A L.Statistical mechanics of complex networks［J］.Reviews of Modern Physics，2002，74(1):47－97.

［18］ Newman M E J.The structure and function of complex networks［J］.Siam Review，2003，45(2):167－256.

［19］ 汪小帆，李翔，陈关荣.复杂网络理论及其应用［M］.北京:清华大学出版社，2006:1－15.WANG Xiao－fan，LI Xiang，CHEN Guan－rong.Complex network theory and its application［M］.Beijing:Tsinghua University Press，2006:1－15.(in Chinese)

［20］ 郭雷，许晓鸣.复杂网络［M］.上海:上海科技教育出版社，2006:27－34.GUO Lei，XU Xiao－ming.Complex networks［M］.Shanghai:Shanghai Science Education Press，2006:27－34.(in Chinese)

［21］ 章忠志，周水庚，方锦清.复杂网络确定性模型研究的最新进展［J］.复杂系统与复杂性科学，2008，5(4):29－46.ZHANG Zhong－zhi，ZHOU Shui－geng，FANG Jin－qing.Recent progress of deterministic models for complex networks［J］.Complex Systems and Complexity Science，2008，5(4):29－46.(in Chinese)

［22］ 李果，高建民，高智勇.基于小世界拓扑模型的复杂系统安全分析［J］.机械工程学报，2008，44(5):86－91.LI Guo，GAO Jian－min，GAO Zhi－yong.Safety analysis of complex system based on small world topological model［J］.Chinese Journal of Mechanical Engineering，2008，44(8):86－91.(in Chinese)

［23］ Pecora L M，Carroll T L.Master stability functions for synchronized coupled systems［J］.Physical Review Letters，1998，80(10):2109－2112.

［24］ Wang X F，Chen G R.Synchronization in scale－free dynamical networks:robustness and fragility［J］.IEEE Transactions on Circuits Systems，Ⅰ:Fundamental Theory Applications，2002，49(1):54－62.

［25］ Atkinson S R，Moffat J.The agile organization:from informal networks to complex effects and agility［R］.US Department of Defense，Command and Control Research Program，Washington，DC，2007:137－155.