滑翔式飞行器再入弹道设计*

刘 欣，李建林，葛健全，杨 涛

（国防科学技术大学航天与材料工程学院，长沙 410073）

0 引言

滑翔式飞行器通常为升力体或乘波体外形的再入飞行器，依靠自身的高升阻比外形，利用空气动力控制飞行轨迹，实现远距离的非弹道式再入机动飞行。由于在增大射程、突破导弹防御系统、再入段机动等方面具有优势，滑翔式飞行器成为近来的研究热点。

国内外在飞行器再人轨迹优化方面已经做了大量研究工作，取得了令人注目的成果。采用优化方法得到再入弹道，在飞行器总体性能分析方面十分有用。但优化计算需要花大量的时间迭代寻找最优控制量及相应的最优轨迹，具有一定的局限性。另外优化算法得到的弹道往往呈跳跃形式，高度振荡变化，不利于控制系统的设计。文中提出了一种方案弹道设计方法，能快速的为制导系统设计提供一条参考弹道，对于制导控制方案设计而言，需要的参考弹道，应是满足约束并且可行的弹道，无须追求某一性能指标的最优。

(1) 通过对水化学数据分析发现，中谷水热活动区热水以HCO3-Na型水为主，浅部地热井水与自然出露的温泉具有相似的水化学特征，深部地热井水ZGJ04与其余点存在明显差别；由Na-K-Mg三角图发现，研究区水样均处于未成熟水区域，并显现出冷水混合的特征。

1 滑翔式再入弹道设计问题

1.1 弹道特征

滑翔飞行器飞行距离远，根据其弹道特征，可将整个再入弹道分为下降段、滑翔段、修正段和末制导段。初始下降段是指从再入点到滑翔开始点的弹道，高度约在30～100km范围，此段大气密度很小，气动力控制能力有限，无法维持滑翔飞行，飞行器必然处于下落状态。初始下降段弹道设计的目的是使弹道能平滑的转换到滑翔状态。滑翔段是再入飞行的主要阶段，基本决定飞行器的射程，通过滑翔段的制导飞行，使弹道满足滑翔段终端射程、速度、高度要求。末制导段弹道飞行速度、高度相对较低，不适宜进行滑翔飞行，末制导段弹道要满足末制导装置的工作要求，满足落点参数的要求。另外根据测量装置的需求，可在末制导段之前加入修正段以修正弹道。

基于图像处理技术的浮冰破碎跟踪试验研究……………………………… 韩 雷，王秀芬，任明轩等(11.53)

1.2 再入动力学方程

考虑地球为旋转圆球，在半速度坐标系建立质心动力学方程，方程的具体形式可见文献[1]。

1.3 弹道设计约束

主要考虑两种约束：终端条件约束和过程约束。

根据高度速度曲线预估航程，目前还没有合适的公式，因此需要得到相应的控制指令，积分三自由度运动方程，得到航程。滑翔段侧倾角指令主要用于侧向弹道控制，可取常值，攻角指令按下式在运动方程积分中实时计算获得：

(1)常见典型的混合油黏度预测模型中，相关常数(如Cragoe中C值，Lederer中α值)表征原油性质，对于不同地区或组分相差较大的原油应有所区别。

之所以采用二段三次曲线的形式是因为三次多项式已足以体现滑翔段起点和终点的速度、高度、速度倾角的要求，此外，采用二段三次多项式的标准轨迹光滑、连续，能较好的反映滑翔弹道的特征，一阶导和二阶导也十分容易得到，减小了跟踪方法设计的难度。实际上滑翔段的弹道也可以设计成直线，但这样一来，一旦控制点改变，则滑翔段起点和终点的也改变，为保证曲线的光滑，不能再选择倾角为零作为各段弹道的分界点，分界点的参数都需要迭代获得，增加了弹道设计的难度。弹道设计成二次曲线也存在类似问题。而若将弹道设计成高次多项式形式，则在求解多项式系数方面又增加了难度。

弹道设计时，必须保证飞行器沿标准弹道飞行能击中目标并满足各项弹道约束。

在调整系数k1、k2选定的情况下，攻角指令由给定的高度速度曲线决定，而高度速度曲线由控制点决定，一旦给定控制点参数，则控制指令也就确定，总航程也就确定了。

1.4 设计目标

滑翔式再入弹道的设计是一个复杂的过程，其主要设计目标是：

末制导段起点即滑翔段终点，其速度倾角可视为0°，末制导段起点的高度通常根据末制导设备的要求确定，在末制导段起点高度确定的情况下，末制导段起点速度Vf0与末制导段常值攻角αf0决定了落速与落角的取值，且在一定范围内，落速随Vf0单调变化，落角随αf0单调变化。因此采用割线法迭代可确定出使落速恰好为Vf、落角恰好为θf的Vf0、αf0。迭代格式如下：

1）根据任务需求，使弹道能准确的命中目标，且满足落点参数要求。

另有研究显示，CgA在NEN细胞的胞质中表达不一致，在某些器官或组织，例如肺、直肠、阑尾等不表达[10]，因此在2013年的美国国立综合癌症网络(NCCN)指南中将其列为诊断NEN的3类证据[11]。而SCGN在直肠、阑尾等部位的NEN中表达，在肺NEN中也呈阳性表达，阳性表达率几乎达到100%。本研究结果显示，在胃和胰腺NEN，SCGN和CgA均高表达，但在肠道NEN中9例SCGN阳性，而CgA均呈阴性表达，提示SCGN联合CgA诊断GEP-NEN可更好地提高检出率。

2）整个再入弹道都应满足各种限制条件，同时还要兼顾飞行器的机动能力。

2 弹道设计方法

2.1 下降段弹道设计

在下降段中，气动力作用微弱，动压、过载均不构成约束。且控制量的变化对初始下降段的飞行影响很小，为减少姿态变化，可采用定攻角和定倾斜角的方法飞行。随着高度的下降，气动力逐渐增大，弹道逐渐拉起直至维持滑翔飞行。从减小热流和增大射程两方面考虑都应使弹道拉起点尽量高，此段攻角指令采用最大攻角αmax。下降段常值倾斜角指令v0会影响弹道拉起点即滑翔段起点的高度，从而影响射程。文中射程的调整统一在滑翔段实现，下降段的常值倾斜角v0取0°，使弹道拉起点尽量高。

因此，下降段弹道的控制量基本确定，无需迭代设计，在弹道计算中，当倾角为零时，认为下降段结束，记录下降段终点 （Vd，Hd）。

2.2 末制导段弹道设计

末制导段弹道必须保证最终命中目标并满足落速与落角的约束。实际飞行中，末制导段为导引弹道，其攻角、侧倾角指令由末制导律产生，基准弹道设计时使用常值攻角和0°或180°侧倾角来实现弹道。根据落速与落角的约束可确定末制导段起点的速度和末制导段的攻角指令。

图5中模块(1)～模块(3)为3个滤波单元,通过级联后即可形成一个三阶数字低通滤波器,采用40 MHz时钟控制信号,clk_in为时钟信号,data_in为输入的信号,ink为滤波器截止频率调节端口,可通过上位机直接调节,模块(4)为D/A输出模块,输出滤波后的信号。

2.3 滑翔段弹道设计

由前面可知，下降段相对固定，末制导段满足落速和落角要求，则滑翔段弹道设计的主要任务就是调整航程，使弹道通过目标，并保证过程约束得以满足。

滑翔段起点即下降段终点（Vd，Hd）由下降段弹道决定，滑翔段终点即末制导段起点 （Vf0，Hf0）由末制导段弹道决定，滑翔段起点和终点的速度倾角均取为0°，其高度随速度的变化率也为0。引入控制点 （Vc，Hc）以调整弹道，控制点的视为0。将整个滑翔段弹道设计为二段三次H－V曲线，通过控制点的高度、速度大小调整整个滑翔段弹道的形状，使其满足热流、动压、过载等约束，并达到指定的航程。

心理健康教育的根本目标是“助人自助”，因此，在家校合作进行心理健康教育过程中，学校主动建立连接，搭建平台；家长自我学习、自我修炼、自我成长，积极参与；促进学校与家长互动、家长与专家互动，多位链接，利用家长学校的连接作用，改善家庭、学校、社区的教育生态。另一方面也要充分突出学生的主体地位，调动学生的积极性，培养学生主动关注与维护自身心理健康的良好意识，引导学生进行自我教育[4]。

滑翔段起点至控制点弹道满足如下速度与高度的关系式：

3.2 抗炎与免疫调节作用 虽然 MA 的作用机制尚不清楚，但有研究发现对于 CRS，MA 的抗炎作用比抗菌作用更重要[9]。十四元环、十五元环 MA可表现出不同的抗炎及免疫调节能力，包括调节细胞因子、趋化因子的合成，抑制转录因子和炎性细胞因子的基因表达，以及免疫调节炎症细胞、成纤维细胞和上皮细胞等。低剂量、长期（1～3 个月）使用 MA 的治疗方案往往有更好的效果。

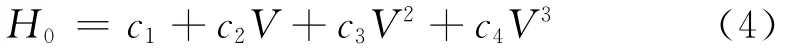
控制点至俯冲点弹道亦为上述三次曲线形式。给定滑翔段起点、控制点的情况下，高度速度曲线满足下列等式，可以解出c1、c2、c3、c4四个系数。

式中：Hd、Hc表示滑翔段起点和控制点的高度；示滑翔段起点和控制点的高度随速度变化率。

2）落点约束。飞行器在一定初始条件下再入飞行，根据飞行任务的需要，要求飞行器的终端弹道参数满足一定的条件，对于导弹来说，通常有落地速度、落地弹道倾角的要求与射程的要求。即：

同样，给定控制点和滑翔段终点，可解出控制点和滑翔段终点的高度速度曲线。

1）过程约束。飞行器再入过程是一个非常复杂的飞行过程，必须考虑热流、动压以及法向过载等因素，即这些因素不能超过飞行器的最大承受能力。通过一定简化，可将约束表示在高度－速度（H－V）剖面内[3]。

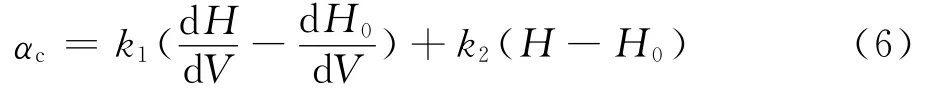
式中：αc表示攻角指令为给定高度速度曲线上的高度和高度随速度变化率为当前弹道实际的高度和高度随速度变化率；k1、k2为调整系数，调整其取值使实际弹道能较好的跟踪给定高度速度曲线。

3）控制量的限制。攻角、侧倾角等控制量的幅值和变化率不能超过限制值。

2.4 侧向弹道控制

对于远距离飞行的飞行器，必须考虑哥氏惯性力和离心惯性力的影响，这两项作用力会引起导弹的侧向运动，在滑翔段的飞行过程中引入常值侧倾角，通过改变侧倾角的符号来控制侧向运动。基准弹道设计时，可通过使侧倾角变号两次的方式来实现弹道，迭代调整侧倾角变号时机，消除侧向运动偏差，使得弹道通过目标。

根据飞行任务需要，还可通过引入侧向误差走廊来控制侧向运动轨迹，实现迂回攻击弹道。详见文献[4]。

3 弹道设计实例

飞行器数据采用美国波音公司1998年设计的再入机动飞行器CAV－L的相关参数[6]。取再入点高度80km、速度5000m／s、速度倾角0°。落点速度要求为800m／s以上，落角要求为80°以上。弹道起点经纬度均为0°，目标点经度为0°，纬度为22.48°。最大热流限制：˙Qmax＝3000kW；最大动压限制：qmax＝400kPa；最大过载限制：ny，max＝6。

下降段攻角取最大攻角20°，侧倾角为0°。以速度倾角为零时刻作为下降段终点，积分三自由度弹道方程可得Vd＝4614.7m／s，Hd＝31.5km。下降段弹道曲线与速度曲线如图2、图3所示。

本文基于云、雪和其他地物在高分四号卫星图像上的光谱响应特征差异，充分利用高分四号卫星高重访观测特性以及全色多光谱成像的优势，提出雪盖提取技术方案，主要技术路线图1所示.

这个嘛，自然是“柿子要拣软的捏”啦！初二学生的心理防线相对其他年级的学生要脆弱得多，比较容易被我“攻击”。

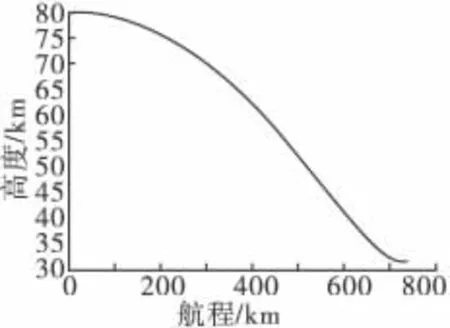
图2 下降段弹道曲线

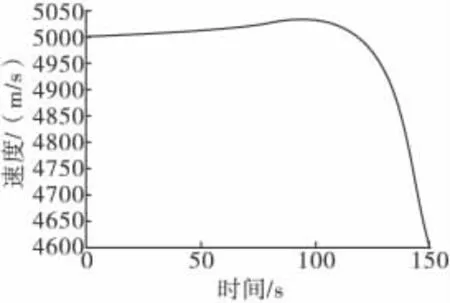
图3 下降段速度曲线

末制导段起点高度取为20km。通过迭代可得，在末制导段初速1130m／s，攻角－10.5°，侧倾角0°的情况下，落点参数恰好满足要求。则Vf0＝1130m／s，Hf0＝20km。末制导段的速度与倾角变化曲线如图4、图5所示。

图4 末制导段速度曲线

图5 末制导段倾角曲线

滑翔段用于侧向弹道控制的常值侧倾角取为30°。先取控制点为 （ （Vd＋Vf0）／2，（Hd＋Hf0）／2） ，确定一组合适的系数k1、k2，使实际弹道能较好的跟踪给定高度速度曲线；然后在满足约束的情况下，调整控制点，使总航程为指定值；然后调整侧倾角的变号时机，控制侧向运动；调整侧向运动会引起总航程的少许改变，最后需要重新微调控制点调整纵向弹道，经过几轮迭代后达到所需的精度。如图6～图9所示。

图6 H－V剖面内弹道与约束

图7 不同航程弹道的实现

图8 侧向运动的调整

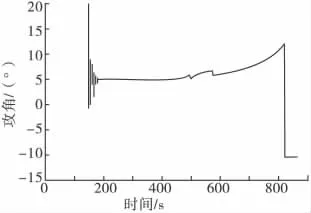
图9 跟踪弹道的攻角曲线

4 结束语

文中根据滑翔式飞行器的弹道特征，将其整个再入弹道分为下降段、滑翔段和末制导段，给出了全再入弹道的设计方法。该方法简单易行，思路清晰，能快速得到一条针对某一飞行任务的弹道，且设计中兼顾了再入弹道的可飞性和可控性，得到的弹道比较平滑，可用于制导控制系统设计。但由于采用二段三次H－V曲线的形式来调整弹道，调整能力受限，无法完成最大射程弹道计算等导弹总体性能分析任务。

[1]赵汉元.飞行器再入动力学和制导[M].长沙：国防科技大学出版社，1997.

[2]郑总准，谢富强，王永骥.高超声速飞行器多约束参考轨迹快速规划算法[J].计算技术与自动化，2009，28（1）：88－91.

[3]闫晓东，唐硕.亚轨道飞行器返回轨道设计方法研究[J].宇航学报，2008，29（2）：467－471.

[4]Shen Zuojun，Lu Ping.On board generation of three－dimensional constrained entry trajectories[J].Journal of Guidance，Control and Dynamics，2003，26（1）：110－121.

[5]Shen Z，Lu Ping.On board entry trajectory planning expanded to sub－orbital flight，AIAA2003－5736[R].2003.

[6]Philips T H.A common aero vehicle（CAV）model，description，and employment guide[R].Report from Schafer Corporation for AFRL and AFSPC，Jan.2003.