改进型BP网络PID在电动舵机控制中的应用*

张 元，周长省，郑 健

（南京理工大学机械工程学院，南京 210094）

0 引言

弹用电动舵机目前大都使用无刷直流电动机（BLDCM），传统的BLDCM系统一般采用PID控制，但面对复杂的非线性系统，PID参数不易整定[1]。BP网络属于前馈型人工神经网络，可以根据在线信息的正向传播、误差反向传播、记忆（权值）训练和学习收敛四个过程，在线修正连接权，使误差沿梯度方向下降，最后使控制进入稳定状态。

文中采用BP神经网络的PID对电动舵机进行转角位置控制，并在此基础上进行了改进。仿真结果表明，改进后的BP神经网络PID控制方法反应快，无超调，与传统PID控制方法相比具有更好的动静态性能、控制精度以及鲁棒性。

1 电动舵机的数学模型

文中以“120°导通型”开关方式为例，分析电动舵机的数学模型。为了便于分析，假定[3]：

1）三相绕组完全对称，气隙磁场为方波，定子电流、转子磁场分布皆对称；

2）忽略齿槽、换相过程和电枢反应等的影响；

3）电枢绕组在定子内表面均匀连续分布；

4）磁路不饱和，不计涡流和磁滞损耗；

5）转子上无阻尼绕组，永磁体也不起作用。

根据基尔霍夫电压定律得定子各相的电压方程为：

式中：ua、ub、uc为定子相绕组电压；ea、eb、ec为定子相绕组的电动势；ia、ib、ic为定子每相 绕 组 的电流；r1为定子每相绕组的电阻；Ls为定子每相绕组的自感；Lm为定子任意两相绕组之间的互感。

由于定子绕组采用星型连接，且无中线，故有：

于是有：

将式（2）代入式（3）得无刷直流电动机数学模型的状态空间表达式为：

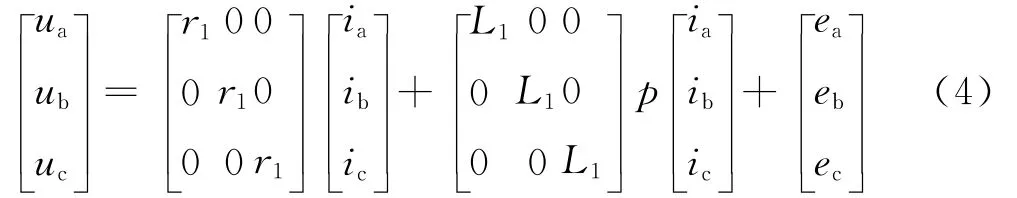
式中：L1＝Ls－Lm为定子每相绕组的等效电感；p为微分算子，p＝d／dt。

电磁转矩方程：

式中：Tem为电机提供的转矩；ω为电机转速。

动力学方程：

式中：TL为负载转矩；J为折算到电机轴上总的转动惯量。

2 BP神经网络PID控制器设计

基于BP网络的PID控制器结构如图1所示，控制器由两部分构成，其中经典的PID控制器直接对被控对象进行闭环控制，并且3个参数kp、ki、kd为在线调整方式；而在线调整的任务由BP网络完成，即根据系统运行的实时数据rin（k），yout（k），error（k）按照BP算法调节PID控制器的参数kp（k）、ki（k）、kd（k），以达到性能指标的最优化。其中BP网络的结构如图2所示，BP网络设置为3层，网络结构为

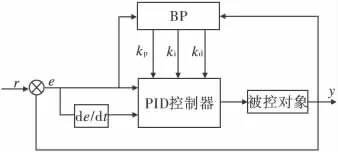
图1 基于BP网络的PID控制器结构

图2 BP神经网络结构

2.1 控制算法

基于BP网络整定PID控制的算法描述如下[4]：

1）确定BP网络的结构，即确定输入层节点数和隐含层节点数，并确定各层加权系数的初值w（1）ij（0）和，选定学习速率的初值η，此时k＝1；

2）采样得到rin（k）和yout（k），计算误差error（k）＝rin（k）－yout（k）；

3）计算BP网络各层神经元的输入、输出，输出层的输出即为PID控制器的三个可调参数kp、ki、kd；

4）根据PID的控制算法，由PID参数kp（k）、ki（k）、kd（k），计算PID控制器的输出u （k）及Δu （k）；

6）置k＝k＋1，返回到2）。

2.2 局限及改进

BP网络由于其很好的逼近非线性映射的能力，因而它可用于信息处理、图像识别、模型辨识、系统控制等多个方面。对于控制方面的应用，其很好的逼近特性和泛化能力是一个优点[5]。而收敛速度慢却是一个缺点，这一点难以满足具有适应功能的实时控制的要求，文中就BP算法的缺点提出了两点改进：

1）加惯性项。为了使收敛速度更快，可在加权系数修正公式中增加一个惯性项，使加权系数变化更平稳。故可改为：

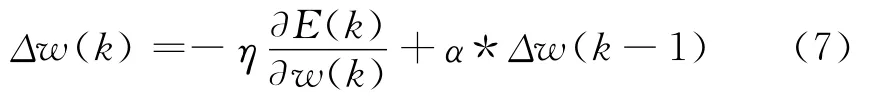
式中：α为惯性系数。

2）加比例系数。由于可调参数kp、ki、kd均取非负的Sigmoid函数，其值在（0，1）之间，使得本算法的应用具有局限性，故加入一个比例系数k，使kp、ki、kd可以在更大的范围内调整，变为：

3 仿真研究

文中采用的电动舵机参数为：额定功率120W，额定转矩0.062N·m；额定转速15600r／min；额定电压24V；额定电流4.75A；转动惯量8.91g·cm2；转矩常数0.013N·m／A；机械时间常数1.59ms；每相电阻0.329Ω；每相电感0.0308mH；磁极对数2；相数3。给电机一个20°的偏转信号，仿真结果见图3～图6。

图3 常规BP网络PID阶跃响应曲线

图4 传统BP－PID参数变化曲线

图5 阶跃响应曲线对比

图6 改进BP－PID参数变化曲线

从仿真结果可以看出，对于常规BP网络PID控制器（见图3），由于受到参数kp、ki、kd在（0，1）之间的限制，对电机转角信号响应很慢，误差跟踪能力很差，调节时间达到了9s，远远不符合电机转角控制的要求。常规PID控制器（见图5）虽然上升时间很快，但上升有震荡，而改进型的BP网络PID控制器改善了这些不足，通过图5和图6可以看出，PID参数变化的范围更大，上升时间更快，动态性能更好。

由此证明，基于无刷直流电机的转角控制，对传统BP网络PID控制器的改进是行之有效的。

4 结论

文中设计了一种改进的BP神经网络PID控制系统，实现了对电动舵机的位置控制。针对传统算法的不足，对其进行了改进，加入了惯量项和比例系数，通过仿真对比发现，该方法响应快、超调量小、鲁棒性强，动态特性明显优于传统PID控制。

在BLDCM这类高度非线性系统中，采用神经网络是极有前景的，它具有提高系统快速性、稳定性和鲁棒性的潜力。神经网络作为人工智能控制的重要分支，将会在实际中获得更加广泛的应用。

[1]K J Astrom，T Hagglund.The future of PID control[J].Control Engineering Practice，2001，9（11）：1163－1175.

[2]王凌，刘卫国.基于模糊PI控制的无刷直流电机调速系统仿真[J].计算机仿真，2009，26（10）：186－189.

[3]曹菁，朱纪洪.电动舵机模糊自适应PID控制研究[J].微电机，2007，40（10）：89－92.

[4]刘金琨.先进PID控制 MATLAB仿真[M].2版.北京：电子工业出版社，2001.

[5]李国勇.智能预测控制及其 MATLAB实现[M].2版.北京：电子工业出版社，2010.