平板封头圆柱形爆炸容器振动特性分析*

年 岗，顾晓辉，成凤生，曾星星

（南京理工大学机械工程学院，南京 210094）

0 引言

爆炸容器是爆炸实验中常见设备，主要结构包括壳体、平板或椭圆封头及法兰盘等。这些结构件与内爆炸冲击载荷会发生复杂的相互作用，从而引起振动。这些振动不仅关系到结构件的工作性能，也影响着其寿命和强度，因此探索爆炸容器的振动规律，对于提高其设计制造水平和安全使用情况，具有重要的现实意义[1－2]。一般而言，为节省经费，对于设计当量不大的爆炸容器，可以采用带有加强筋的平板封头[3]。

文中拟对某一平板封头圆柱形爆炸容器的壳体振动响应进行分析研究，该容器设计当量为50gTNT，它由两块标准的平板封头和一段圆柱形壳体焊接相连，长0.8m、内径0.8m、壁厚12mm、平板封头厚度20mm，其结构见图1。采用柱状钝化黑索今炸药在中心点爆炸加载的方式，监测壳体外表面3个测点的振动加速度波形，并分析容器壳体在不同强度冲击载荷作用下的振动特性。

图1 容器结构与测点布局图

1 测点布局与测试系统

1.1 测点布局

实验共布有3路加速度测点。加速度测量在壳体中环面上的小法兰盘中心设置一个测点，如图1中A点，在壳体上方设置测点B，其水平方向上距A点0.2m，而在距A点0.3m同一水平方向上的大法兰盘中心设置测点C。压力测量在靠近B点处设置测点D，测点布局见图1。

1.2 测试系统简介

测试系统主要由压力传感器、加速度传感器、内嵌式数据记录仪及计算机等组成。根据以往的实验经验来选择合适的加速度计，A点、B点选用JF100C型加速度计，C点选用型加速度计，D点型压力传感器。加速度传感器采样频率均为250kHz，压力传感器采样频率为500kHz。

图2 测试系统示意图

2 测试结果与分析

2.1 圆柱壳体固有频率分析

容器外径与内径比小于1.1，所以适用薄壳理论[4]。设圆柱壳体内径为R，长度为L，h为壁厚，E为壳体材料杨氏弹性模量，ρ、μ为材料密度和泊松比。选用柱坐标系，轴向、环向、法向分别用x、φ、z表示，设中面上一微元P受到力N、力矩M和剪力Q、S的作用时，轴向、环向、径向的位移分别为u、v、w，建立如图3的坐标系。微元P受力如图4所示，设在x面上（x为常量的横截面上）拉应力为Nx；纵向剪力为Sxφ；作用于单位宽度上的横向剪力为Qx；弯矩为Mx；扭矩为 Mxφ。

图3 容器柱坐标系

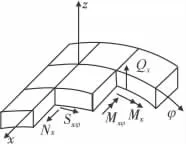
图4 微元受力示意图

圆柱薄壳平衡微分方程如下：

式中：X、Y、Z分别为微元P 轴向、环向、径向所受的外载荷和约束反力，壳体产生自振时上式中X、Y、Z分别取：

Donnell简化理论是振动分析中应用最为广泛的一种简化方法，它假设在平衡微分方程中，只考虑Z方向的惯性分量而忽略X、Y方向惯性分量和剪切力项，并引入应力函数Φ（x，φ），且满足：

基于以上的假设，对式（1）平衡方程进行推导，得到Donnell方程式：

式中：D为圆柱薄壳的弯曲刚度，∇2、∇2k为微分算子：

实验用圆柱形爆炸容器两端为简支闭口，故端面可视为剪力薄膜，即端部边界各点径向和环向的位移被阻止，转动和轴向位移是自由的，其边界条件为：

在两端简支的条件下，中面微元的位移解可以用三角函数表示，设振型函数为：

式中：m为轴向模态阶次或半波数，n为环向模态阶次或波数。将振型函数代入式（4），得到振型方程[5]：

解得角频率为：

从上式可以明显看出角频率是由两部分组成的：第一部分由薄膜振动引起；第二部分则对应着弯曲振动，当m及n增加时弯曲振动逐渐占主导地位。

考虑到两端封头的约束作用，取m＝1，n＝1，2，3，…，18。将结构参数和材料特性参数代入式（9）计算，则角频率公式化简为：

可以得到圆柱壳体固有振动频率，见表1。

表1 圆柱壳体各阶固有振动频率（m＝1）

2.2 内爆炸冲击载荷频谱分析

实验对容器壳体中环面处的反射超压进行了测量，测点D在3.6g、5g和10g药量下的反射超压波形及相应频谱图如图5所示。由实测信号波形及相应的频谱图可知，中心点爆炸在容器壳体上产生的冲击波载荷具有脉冲特征，冲击载荷在壳体振动的整个频率范围内（10kHz以内）的频谱具有超带宽特征，分布均匀且无明显峰值。因此认为壳体的振动频率不受冲击载荷的影响，而主要相关于壳体自身的固有频率[6]。

图5 3.6g和10g药量时测点D处反射超压波形及频谱分布

2.3 圆柱壳体实测响应的频谱分析

内爆炸冲击中的振动信号属于非周期平稳信号，选择FFT算法对其进行功率谱分析。图6、图7所示为测点A及测点分别在3.6g、5g和10g三种药量下的振动加速度波形图，而图8、图9为对应的频谱图。

图6 测点A加速度信号波形图

图7 测点C加速度信号波形图

图8 测点A加速度信号的频谱波形

图9 测点C加速度信号的频谱波形

在实验药量范围内，由统计的频谱波形可以看出，壳体振动频率范围较宽，主要分布在前11阶固有频率内。

由图6和图7分析得知，中环面（与装药同一截面位置）上测点A处所受爆炸载荷最大，而远离中环面的位置测点C由于距离增加和角度的变化，载荷不断下降。

由表1和图8可知，在实验药量范围内，中环面测点A处振动以高阶固有频率（弯曲振动频率）为主，并且随着实验药量增大幅值也在增大，说明容器壳体吸收的振动能量在增加，特别是呼吸振动频率（n＝1，m＝1）附近的频率成分明显增多，振动主频有向其靠近的趋势。从角频率公式可以看出，增大半径可以提高呼吸振动频率，而使振动频率远离呼吸振动频率可以避免谐振，提高容器的安全性能。工程实际中采用在中环面外侧焊接加强层的方法来实现，同时又能减轻重量和节约经费。

由表1和图9可以看出，在实验药量范围内，测点C低阶固有频率（薄膜振动频率和非轴对称弯曲振动频率）成分较多且峰值明显，说明远离中环面的壳体振动主频主要以低频为主，且低药量时低频谱线较多，说明低频成分更易被激发，引起的谐振会影响容器的安全。分析认为，这些低频振动的产生主要是由于壳体结构并非完全的对称造成的，特别是在壳体表面开有大小不一的传感器孔、观察孔和清扫孔，此外装药位置的偏心也是原因之一。所以为提高爆炸容器的安全性能，壳体上实验用的孔或盘类结构应尽量选在靠近中环面处开设。

3 结论

由圆柱壳体固有振动模态分析以及实测得到的壳体振动频谱可以得到以下结论：

1）实验证实了内爆炸冲击载荷具有脉冲特征，频谱具有超带宽特征，分布均匀无明显峰值，说明壳体振动频率不受冲击载荷的影响，主要由壳体结构本身固有频率决定；

2）在实验药量范围内，由实测信号频谱分析表明，壳体振动频率范围主要分布在11阶以内；

3）靠近中环面的壳体振动主频以高阶固有频率为主，且随冲击载荷的增大有向呼吸振动频率靠近的趋势。工程实际中可以采用在中环面外侧焊接加强层的方法提高呼吸振动频率，从而避免谐振提高容器的安全性能；

4）远离中环面的壳体低阶固有频率更易被激发，引起的谐振会影响容器的安全。通过减少壳体非对称结构，将壳体上孔或盘类结构开设在中环面附近的办法来减少这种影响。

[1]Duffy T A，Mitchell D.Containment of explosions in cylindrical shells[J].Int J.Mach Sic，1973，23（2）：215－237.

[2]钟方平，陈春毅，林俊德，等.带平板封头的双层爆炸容器动力响应的实验研究[J].爆炸与冲击，1999，19（3）：199－203.

[3]赵士达.爆炸容器[J].爆炸与冲击，1989，9（1）：85－96.

[4]曹志远.壳体振动力学[M].北京：铁道出版社，1989.

[5]陈铁云，陈伯真.弹性薄壳力学[M].武汉：华中工学院出版社，1982.

[6]霍宏发.椭球封头圆柱形爆炸容器振动特性研究[J].机械科学与技术，2000，19（6）：968－969.