一种比例尺蒙特卡罗滤波算法＊

赵 新，宁小磊，梁 兴

（中国华阴兵器试验中心，陕西华阴 714200）

0 引言

随着计算机技术的发展，一种基于Monte Carlo方法的粒子滤波器［1－13］（particle filter，PF）为解决非线性非高斯滤波问题提供了新途径，其基本思想是用一组带有权值的粒子集表示解决问题时需要的后验概率密度，然后用这一近似的表示来计算系统的状态估计［3］。然而，在粒子滤波器的设计过程中，普遍存在计算量较大和粒子退化等问题，限制了其在工程领域中的实际应用。常用的解决退化问题的方法有重采样和适当选取建议分布。重采样虽然在一定程度上可以解决粒子退化问题，但却因此带来了粒子枯竭的问题。为此，文中提出了一种新的比例尺粒子滤波算法（scale particle filter，SPF）。该算法按粒子重要性权值将粒子集划分成好（重要性权值大）粒子群和较差（重要性权值小）粒子群，然后对好粒子和差粒子求取比例尺加权值，从而生成一些备选粒子，并通过重要性权值的优选实现重采样后粒子集多样性的增加。

1 基本粒子滤波器算法及其缺陷

设非高斯、非线性随机状态空间模型为［5－9］：

式中：xk和zk分别是k时刻的系统状态变量和量测值；映射分别是系统状态转移模型函数和量测模型函数；ωk和vk分别是过程噪声和观测噪声。状态估计问题描述可归结为利用所有可能得到的观测序列递归的估计当前时刻状态xk的后验概率分布由于包括序贯估计的完全信息，进而可得到系统状态估计所需参数如均值、方差等信息。）一般由下列方法可以得到：

然而，式（2）～式（4）所示Bayes递推过程中的积分一般不可积。粒子滤波通过采用Monte Carlo采样技术实现了上述积分运算，具体过程可描述为以下两个阶段：

1中随机抽取的样本。

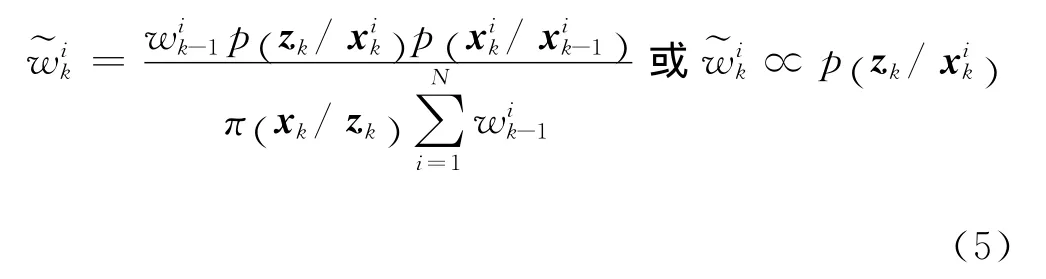
图1给出了基本粒子滤波器算法的迭代过程。

图1 基本粒子滤波器方法

建议分布的选取是设计粒子滤波的关键技术之一，它对滤波算法效率的影响是明显的，尤其关系到粒子权值的退化速度。Doucet［13］等给出了一个最优的建议分布它能使粒子权重的方差为0，但遗憾的是一般从中抽样是困难的。在实际应用中，建议分布通常选取为先验状态转移概率的形式，它使粒子的采样和权值的递推计算容易实现，但没有引入系统最近观测信息，具有一定的盲目性，容易引起粒子退化，使得重要性采样后粒子重要性权值方差加大，多数粒子的权值趋于0，只有少数粒子的权值趋于1。这就浪费了有限的计算资源，降低了系统状态的推理精度。克服退化问题的一个有效方法是在权重规格化处理后，根据权重进行重采样。重采样过程将权重高的粒子复制多份，权重微小的粒子则被删除，粒子被复制的概率与权重成正比，从而把计算资源按照粒子权值进行分配。但重采样容易引起粒子多样性的丧失，使大量粒子成为权值较大粒子的子代，极大减少了参与估计的支撑集样本，引起粒子枯竭现象，降低了滤波效果。

2 比例尺粒子滤波器算法

样本集“多样性”变差会导致粒子滤波出现退化现象，以下给出一种改善样本集多样性的策略，使好样本被保留参与状态估计，以提高粒子滤波的估计与跟踪能力。

2.1 算法思想

比例尺粒子滤波算法的基本思路是：在重要性抽样后，将粒子集按权值递增的顺序进行排序；然后，选择一些权值较大的粒子作为榜样群，剩余的粒子作为候选粒子；接着，对榜样群和候选群中的粒子序贯求取以初始设置的比例尺为参数的加权值，生成一些候选粒子；最后，依据粒子重要性权值对重要性抽样生成的候选粒子和比例尺加权生成的粒子实现粒子优选。优选法则为：重要性权值大者，优选晋级；重要性权值小者，优选失败，给以淘汰。

2.2 算法步骤

比例尺粒子滤波算法描述如下：

步骤2重要性采样。当k≥1时：

3）按粒子重要性权值将粒子集划分为好粒子集和较差粒子集

其中：xk′为好粒子群；N′为好粒子的个数；xk″为较差粒子群；N″为较差粒子的个数。它们的确定方法可以初始设置时给以确定，也可以根据粒子退化情况动态自适应的确定。

4）比例尺加权求取备选粒子

方法是从好粒子群选择一个最好的粒子，然后序贯的从较差粒子群中抽取粒子按下式以生成备选粒子：

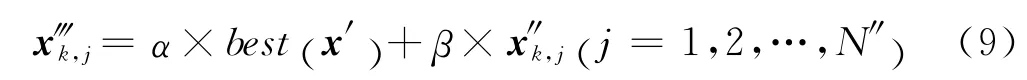
5）计算粒子权值

6）归一化权值

7）优选粒子

步骤4结果输出。按下式对结果进行估计：

其中：δ（）·为在xik的狄拉克delta函数。

步骤5令k＝k＋1，返回步骤2。

2.3 算法分析

1）算法有效性分析。比例尺粒子滤波算法在重要性抽样之后，通过初始设置比例参数，对重要性采样粒子集某些粒子求取加权值，生成一些备选粒子，并通过重要性权值的度量，实现了粒子的优选，使较好的粒子参与状态估计，从而缓解了粒子退化对滤波结果的影响。同时，这些备选粒子包括了粒子集中的好粒子和较差粒子信息，充分利用了粒子滤波的信息，所以能够最大限度的改进粒子滤波性能。

2）算法复杂度分析。比例尺粒子滤波算法，仅在重要性抽样之后对某些粒子实行比例加权计算，其计算量相对于基本粒子滤波算法仅增加了（）O N″，可见，这种改进策略基本上不增加算法的复杂度。此外，如果基本粒子滤波器没有出现粒子退化现象，可以避过比例尺加权计算步骤，进一步降低运算量。当然，此时运行此步可以提高算法精度。

3）算法实用性分析。比例尺粒子滤波算法原理简单，工程实现方便，但却能有效缓解粒子退化现象对粒子滤波造成的不良影响，因此，很有前景。同时，根据粒子滤波的具体情况，可以一直运行，亦可以根据需要间断运行；此外，比例尺加权系数和参与计算的粒子数也可以根据具体情况自适应的调整。所有这些都反映了比例尺粒子滤波算法的优势，使其更具有工程应用前景。

3 数字仿真

文中使用一个广泛使用的非线性模型检验比例尺粒子滤波算法的有效性。该模型运动模型和观测模型为［8］：

一般用均方根误差（RMSE）来度量粒子滤波算法的误差，单次运行的RMSE按式（14）计算：

多次独立实验时，采用RMSE的均值对滤波结果进行度量，即：

其中：M为滤波迭代步数；Tf为Monte Carlo仿真次数；xk为第k步的状态真值；＾xk为第k步的状态估计。

图2 不同非线性滤波算法产生的状态估计曲线

图3 不同非线性滤波算法产生的RMSE随仿真次数的变化曲线

图2给出了不同粒子滤波器进行一次独立实验所产生的状态估计结果，可以看出，SPF所估计的状态能较好的与真实状态吻合，这说明该算法是有效的。

图3给出了经过100次独立实验、不同非线性滤波算法状态估计的RMSE随粒子数变化的柱状图，可以非常明显地看出：比例尺粒子滤波算法的估计精度优于EKF和基本粒子滤波算法，且滤波器比较稳定。其中，EKF100次估计的，其方差为149.9207；基本粒子滤波算法100次估计的，其方差为0.9359；比例尺粒子滤波算法100次估计的，其方差为0.1808。

4 结束语

粒子滤波器在解决非线性非高斯滤波问题方面具有明显的优势，目前已吸引众多学者进行研究。文中针对粒子滤波的退化和枯竭问题，提出一种新型粒子滤波器——比例尺粒子滤波算法（SPF），该算法通过比例尺加权策略为粒子滤波生成一些备选粒子，并使用重要性权值对其进行了优选，从而得到更好的支持粒子集参与状态估计。仿真结果表明，比例尺粒子滤波在滤波精度和算法稳定性上均优于基本粒子滤波。

［1］Anderson B D O，Moore J B.Optimal filtering［M］.Prentice－Hall，1979.

［2］王法胜，赵清杰.一种用于解决非线性滤波问题的新型粒子滤波算法［J］.计算机学报，2008，31（2）：346－352.

［3］武元新.对偶四元数导航算法与非线性高斯滤波研究［D］.长沙：国防科技大学，2005.

［4］De Freitas.Sequential Monte Carlo methods to train neural network models［J］.Neural Computation，2000，12（4）：955－993.

［5］R van der Merwe，A Doucet，J F G de Freitas，et al.The unscented particles filter［Z］.Adv.Neural Inform.Process.Syst.，Dec.2000.

［6］段琢华，蔡自兴，于金霞.移动机器人软故障检测与补偿的自适应粒子滤波算法［J］.中国科学E辑，2008，38（4）：565－578.

［7］宁小磊，王宏力，张琪，等.区间衍生粒子滤波器［J］.物理学报，2010，59（7）：24－32.

［8］宁小磊，王宏力，宁宇琪，等.高斯衍生粒子滤波器［J］.西安交通大学学报，2010，44（6）：72－77.

［9］Julier S J，Uhlmann J K.Unscented filtering and nonlinear estimation［J］.Proceedings of the IEEE，2004，92（3）：401－422.

［10］Pitt M K，Shephard N.Filtering via simulation：auxiliary particle filters［J］.Journal of the American Statistical Association，1999，94（2）：590－599.

［11］Jayesh H Kotecha，Petar M Djuric.Gaussian sum particle filtering［J］.IEEE Transactions on Signal Processing，Oct.2003，51（10）：2602－2611.

［12］Gordon N J，Salmond D J，Smith A F M.Novel approach to nonlinear/non－Gaussian Bayesian state estimation［J］.IEE Proceedings on Radar and Signal Processing，1993，140（2）：107－113.

［13］Doucet A.On sequential simulation－based methods for Bayesian filtering［R］.University of Cambridge：Technical Report，CUED/F－INFENG/TR.310，1998.