基于BP人工神经网络的末修弹落点预测导引模式＊

曹营军，朱宗平，李立春，邵 毅

（北京特种车辆研究所，北京 100072）

0 引言

由于炮口初始干扰和外弹道各种不确定因素的存在，末修弹实际飞行状态与理想运动状态之间有一定的偏差存在。从运动学的观点看，导引方法能确定弹丸在末修段的理想飞行状态，以获得对目标的最小脱靶量。而弹道点的诸元参数不同时，在同样弹道干扰下，弹丸落点是不同的，即弹道点特征参数决定了弹丸落点。如果根据弹道参数状态确定出弹丸落点，就可以修正弹道参数的方式修正弹丸落点。

文中以GPS全球定位系统为导航体制，以脉冲直接力作用于末修弹质心直接获得对质心速度矢量修正为研究背景，以BP人工神经网络为数学工具对落点预测导引模式进行深入分析研究。

1 落点预测导引模式

1.1 剩余射程预测

落点预测导引模式，是以实际弹道点诸元下弹丸的预测落点与目标点之间的偏差作为弹道偏差量，对速度矢量进行修正的［1］。每次脉冲修正是以减少落点偏差量作为直接目的，该方法的关键是根据当前弹道点的诸元参数建立一个落点预测模型，即剩余射程（当前弹道点与预测落点之间的纵向距离）预测模型。

落点预测的关键是根据实时弹道点的诸元参数建立一个剩余射程预测模型：

式中：A为弹道诸元参数，即剩余射程L的解释变量。

文献［2］中，将弹丸剩余射程预测问题变成了寻找剩余射程与弹道特征参数之间联系的问题。

1.2 解释变量选取

数学模型是处理变量之间相关关系的数学工具，用于研究一个因变量与一个或多个解释变量之间相互的依赖关系，并估计或预测因变量值。因为要建立剩余射程模型，故剩余射程是因变量，解释变量是与剩余射程有关的弹道参数［3－4］。

解释变量的选取应该遵守以下两个原则：一是由于弹载计算机性能的限制，要求选取的解释变量（弹道参数）需与因变量（剩余射程）之间具有较强的相关关系，及相关系数要大；二是敏感弹道参数的技术在工程上要易于实现，且成本不会太高。

导引模式的研究是在质点弹道学的范围内展开的，所以主要分析质点弹道特征参数：位置坐标x、y、z和速度分量Vx、Vy、Vz对剩余射程的影响程度，即相关关系。剩余射程的大小主要受到纵向速度Vx的大小以及弹丸在空中剩余飞行时间t的影响，而剩余飞行时间t主要由竖直方向速度Vy和弹道高y决定。所以，文中尝试取弹道高y、速度分量Vx、Vy为解释变量，建立剩余射程预测模型。

2 BP神经网络剩余射程预测模型

2.1 建立BP人工神经网络

误差反向传播神经网络即BP神经网络以非线性大规模并行处理为基础，由大量神经元经过一定的抽象、简化与模拟形成的大规模、非线性动力学系统，具有人工信息处理模型功用，具有高速运算能力。通过网络训练学习实现非线性函数映射，广泛应用于性能预测、模式识别、模糊控制等过程。

2.1.1 确定BP网络结构

根据Kolmogorov定理［5－6］可知，总存在一个三层的神经网络，能精确实现任意的连续映射f：RN0→RNm。输入层神经元数目由影响剩余射程的因素个数决定，输出层神经元数目只有一个，对应于剩余射程。

由1.2节中分析可知，BP模型输入层神经元N1为3个，分别为弹道高y、水平速度方向分量Vx、竖直速度分量Vy，输出层神经元N3为1个，表示剩余射程L。目前，隐含层神经元节点数尚无统一确定公式，根据文献［5］，确定隐含层节点数N2如下：

当输入层神经元数为N1，输出层神经元数为N3时：

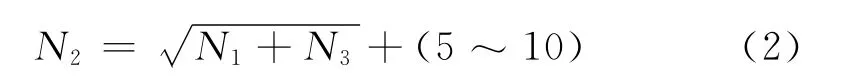
根据上述确定隐含层神经元数的原则，结合剩余射程预测的特点，隐含层神经元数取为8。综上所述，剩余射程预测BP模型取为型，如图1。

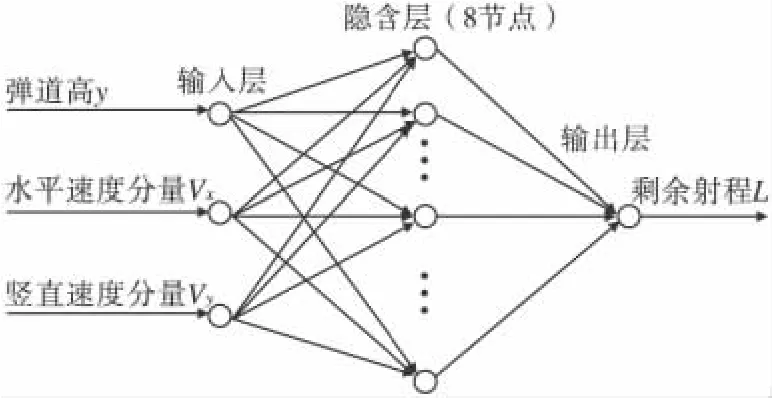
图1 剩余射程BP神经网络预测模型

基于Simulink仿真工具，建立了BP网络训练模型。

2.1.2 BP网络训练

训练学习用试验数据的选取，要能够很强的代表末修段的弹道特性，要最大程度的表现出因变量与解释变量之间的相关性。在各种随机扰动因素作用情况下，结合末修弹射角范围，在10°、15°、20°、25°、30°、35°、40°、45°、50°、55°、60°射角条件下，各进行100条蒙特卡洛模拟打靶试验。数据采集从每条弹道的弹道顶点开始，并结合相对应的剩余射程组成回归数据对，采集数据时间间隔为0.25s。

为提高BP网络的训练速度，BP神经网络的输入、输出值需要作标准化处理，一般将数据归一化到［0.1，0.9］范围内较好，根据文献［7］将数据标准化处理如下：

利用上述的BP网络学习参数和训练模式对，对末修弹的剩余射程模型进行了18395次训练后，得到稳定的BP神经网络模型。

2.1.3 落点预测仿真分析

以2.1.2节中建立剩余射程神经网络预测模型，在45°射角下，在6自由度弹道模型上利用得到的预测模型进行仿真，并和实际剩余射程进行比较，对比效果见图2。

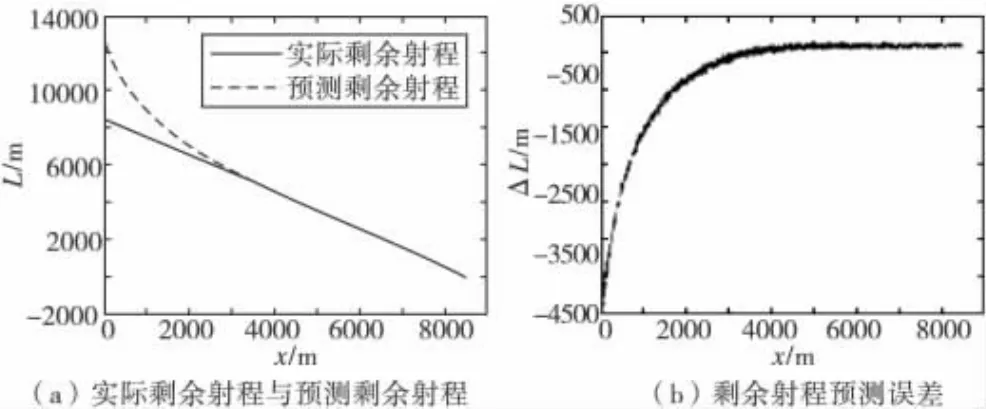
图2 剩余射程神经网络预测模型分析

分析图2可知，神经网络剩余射程的预测值和实际值在弹道前期（弹道顶点前）差别比较大，究其原因是因为神经网络剩余射程模型训练用的试验数据取自弹道后期（弹道顶点后），但前期的模型误差对弹道修正没有实质性影响。

2.2 导引模式分析

落点预测导引模式基于当前弹道参数（y、Vx、Vy）对弹丸落点进行预测，以目标点与预测落点之间的距离为一种广义概念上的弹道偏差。问题的关键是利用建立的落点预测模型，根据实时弹道点的诸元参数预测弹丸落点，根据预测偏差量确定点火脉冲需求数nxy。

剩余射程预测值L为：

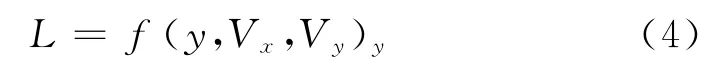
剩余射程实际值L1为：

式中：xT为目标点在惯性坐标系中的纵向坐标。

根据式（4）、式（5），得到预测落点偏差ΔL 为：

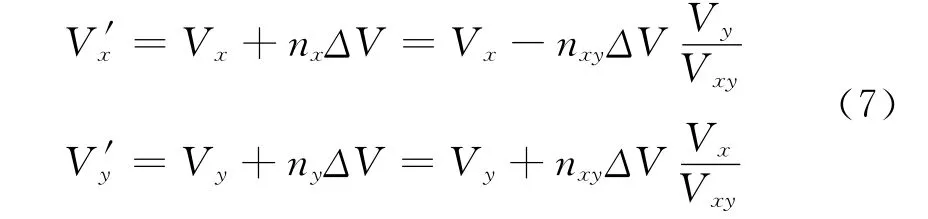
为分析问题简单，认为弹轴与速度方向一致，即攻角为零。脉冲修正后，由于脉冲作用时间短（毫秒级），认为弹丸位置不发生变化，而只是修正了速度矢量，修正后的速度分量如下［1］：利用神经网络法预测弹丸落点时，由于神经网络数学模型是隐性函数，不能得到具体的函数形式，所以不能直接得到脉冲需求数解析表达式。而在文献［1］中，以线性回归法预测弹丸落点得到脉冲需求数nxy为：

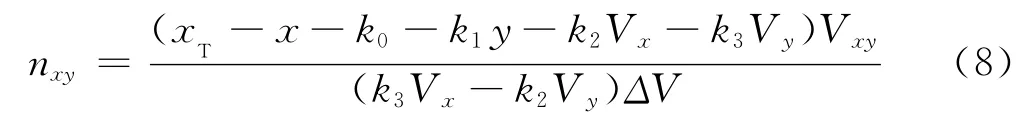
文中结合线性回归法，采用线性插值的方法得到脉冲需求数nxy。以式（8）计算得到的nxy为第一个脉冲需求数，结合式（7）得到修正后的纵向平面内的速度分量，利用搭建的神经网络模型对落点进行预测，如果实际剩余射程有差异，则采用线性插值的方法得到第二个脉冲需求数，再采用模型对剩余射程进行预测，如此反复，直至得到最佳的脉冲需求数nxy。

3 仿真效果分析

分别以回归法射程预测模型和神经网络法射程预测模型，在45°射角下，采用6个40N·s大小的脉冲，分别在无控模式、纵向采用落点预测导引模式（横向采用速度追踪导引模式）下各进行500次蒙特卡洛打靶试验，试验结果见表1，弹丸落点散布见图3。

表1 落点预测导引模式控制效果

分析表1和图3可知，采用基于BP神经网络的落点预测导引模式对末段弹道进行修正时，x向落点散布都明显减小，圆概率偏差CEP都明显降低，落点散布明显集中，说明采用落点预测导引模式对末修段进行控制，能够明显提高末修弹落点精度。

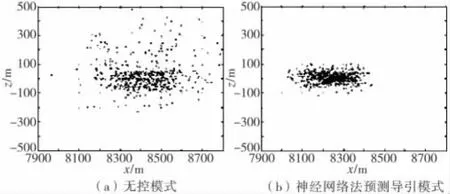
图3 神经网络法落点预测导引模式落点散布效果

4 结论

1）落点预测导引模式可以用于对末修弹进行导引与控制，提高了末修弹落点精度；

2）将BP人工神经网络技术作为数学工具引入末修弹落点预测导引是合理可行的；

3）界定落点预测为一种导引模式，拓宽了导引模式的深度和概念范畴。

结合不同的工程应用背景，对预测模型还需要更深入具体的优化分析研究，以期最大程度的提高末修弹落点精度，提高其综合毁伤能力。

［1］曹营军.基于脉冲控制的修正迫弹制导与控制技术研究［D］.北京：北京理工大学，2008.

［2］张成.远程火箭弹射程控制研究［D］.北京：北京理工大学，2005.

［3］钱杏芳，林瑞雄，赵亚男.导弹飞行力学［M］.北京：北京理工大学，2000.

［4］高惠璇.应用多元统计分析［M］.北京：北京大学出版社，2005.

［5］胡伍生.神经网络理论及其工程应用［M］.北京：测绘出版社，2006.

［6］Hush D R，Home B G.Progress in supervised neural networks［J］.IEEE Signal Processing Magzine，1993，10（1）：8－39.

［7］许禄，胡昌玉.化学中的人工神经网络法［J］.化学进展，2000（1）：18－31.