圆柱形弹丸高速撞击薄板的碎片云特性数值模拟

盖芳芳， 刘先应， 刘 恂， 赵继涛

(1.黑龙江科技大学 理学院，哈尔滨 150022;2.哈尔滨理工大学 建筑工程学院，哈尔滨 150080)

随着人类航天活动的日益增多，空间碎片环境日趋复杂，严重威胁在轨航天器的安全运行[1]。目前，国内外针对空间碎片撞击航天防护的研究主要采用球形弹丸撞击防护结构[2－3]，而空间碎片形状多种多样。研究表明，在相同的撞击条件下非球形弹丸比相同质量的球形弹丸损伤性更大[4－8]，因此，确定弹丸形状对超高速撞击过程的影响非常重要。由于实验费用较高及超高速撞击实验对撞击速度、质量、形状和材料等的限制，超高速撞击数值模拟成为研究防护结构防护性能的有效方法之一[9－11]。笔者采用 AUTODYN －2D 软件对柱形弹丸(国产航空材料Al－2017)超高速正撞击单层薄铝板(Al－2A12)防护结构形成的碎片云进行数值模拟，研究柱形弹丸长径比对碎片云特性的影响。

1 计算模型及数值模拟方案

根据弹丸几何形状的轴对称性，应用AUTODYN－2D轴对称非线性动力学分析软件，采用SPH方法建立圆柱形弹丸高速撞击单层薄铝板计算模型，几何模型如图1所示(由于轴对称，仅需相对于对称轴建立一半弹丸和薄板)。弹丸采用Al－2017铝合金材料，薄板采用Al－2A12铝合金材料，弹丸质量为316 mg，板厚度为1 mm，质点直径为0.1 mm。材料的状态方程采用的是AUTODYN软件数据库提供的Shock状态方程，强度模型采用Johnson－Cook强度模型。为保证绝大部分撞击体材料为固体状态，设定撞击速度为5 km/s。

图1 初始几何模型Fig.1 Initial geometry model

为了研究圆柱形弹丸长径比(L/D，其中，D为弹丸直径，L为弹丸长度)对碎片云特性的影响，在相同质量和速度条件下，选取25组数值模拟工况。弹丸的长径比介于0.1～20.0之间，数值模拟工况的具体参数如表1所示。

表1 数值模拟工况Table 1 Simulation cases

2 结果与分析

2.1 碎片云形态

图2给出了撞击20 μs后不同长径比圆柱形弹丸撞击单层板形成的碎片云形态数值模拟结果。由图2可见，在长径比分别为0.6、1.4与3.0时，碎片云形态发生了较大的改变，并且弹丸长径比不同，弹丸的破碎程度不同。当弹丸长径比L/D＜1.4时，弹丸破碎较好，且有明显的分层;当弹丸长径比L/D＜0.6时，形成的碎片云中弹丸与薄板的材料质量较分散;当弹丸长径比介于0.6～1.1之间时，形成的碎片云中弹丸材料较集中，主要位于弹丸的撞击轴上;当弹丸长径比介于1.4～2.0之间时，撞击后弹丸发生破碎，但破碎并不充分，碎片云中含有较大的弹丸碎片，并且大部分的弹丸与薄板材料位于碎片云前端的弹丸撞击轴上，质量较集中;当弹丸长径比L/D≥3.0时，撞击后弹丸头部发生破碎，后部未发生破碎，保持原有形态，且位于弹丸撞击轴上。

综上所述，当圆柱形弹丸撞击速度、质量相同时，弹丸长径比不同，碎片云形态将发生较大的改变。弹丸长径比越大，碎片云质量越集中;当弹丸长径比L/D≥3.0时，撞击后弹丸有剩余长度，且随着弹丸长径比的增加，弹丸剩余长度增加。

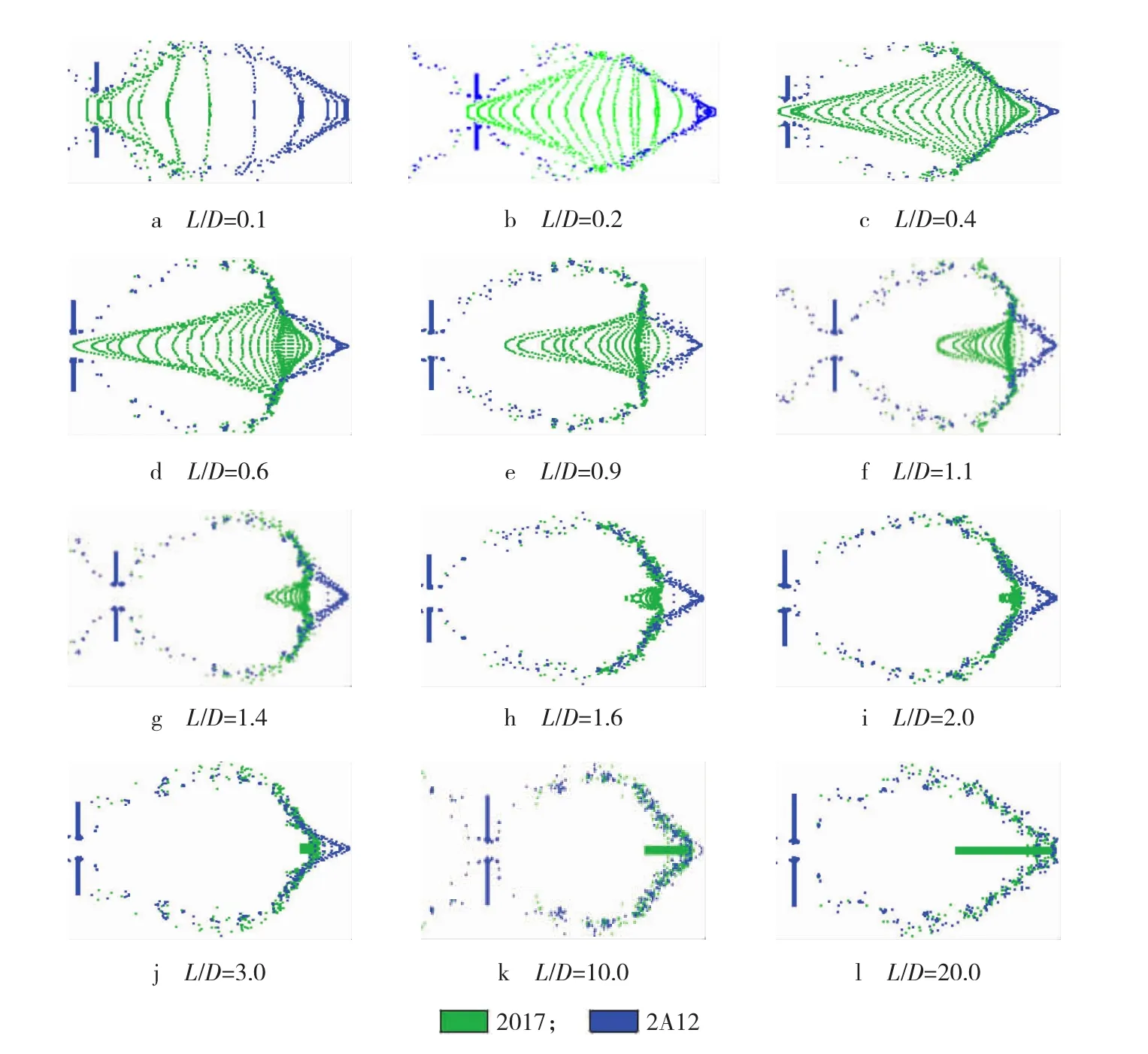
图2 不同长径比圆柱形弹丸高速撞击单层板碎片云形态数值模拟结果Fig.2 Simulation results of debris clouds morphology of thin plates impacted by projectiles with different ratio between length and radius

2.2 碎片云特征参数

2.2.1 尺寸及速度

为进一步分析圆柱形弹丸长径比对碎片云特性的影响，选取碎片云轴向长度、径向扩展直径、前端速度及穿孔直径进行分析。

图3、4分别给出了撞击20 μs后碎片云的轴向长度(L1)、径向扩展直径(D1)、前端速度(v1)随弹丸长径比的变化规律。由图3可见，当弹丸撞击速度为5 km/s时，碎片云轴向长度、径向扩展直径随着弹丸长径比变化不大，基本保持一致。又由图4可见，当弹丸长径比变化时，碎片云前端速度也基本保持一致。由此可知，弹丸长径比对碎片云尺寸、前端轴向速度影响不大。但由图2给出的碎片云形态随弹丸长径比的变化可见，弹丸长径比越大，碎片云质量越集中，碎片云中包含的碎片越大，且均位于撞击轴上碎片云前端，即碎片云前端碎片具有的动能随着弹丸长径比的增加而增大。由以上分析可知，随着弹丸长径比的增加，碎片云前端动能增大，即撞击产生的碎片云对航天器舱壁的损伤能力更强。

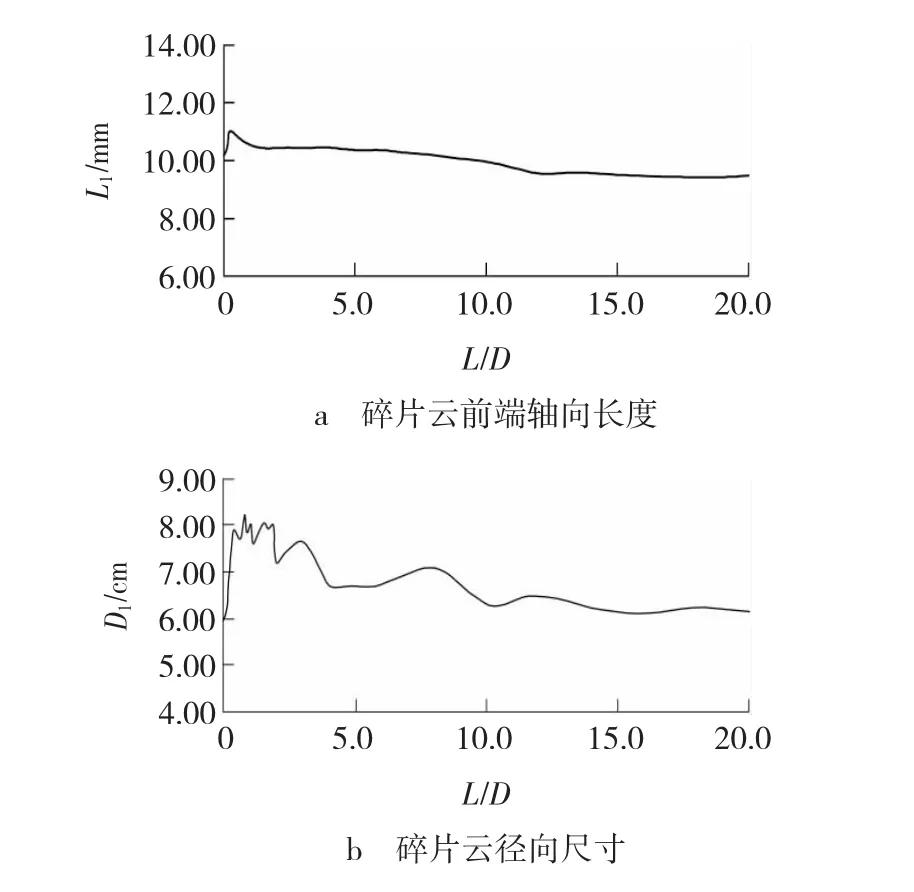
图3 不同长径比弹丸的碎片云尺寸Fig.3 Size of debris clouds by projectiles with different ratio between length and radius

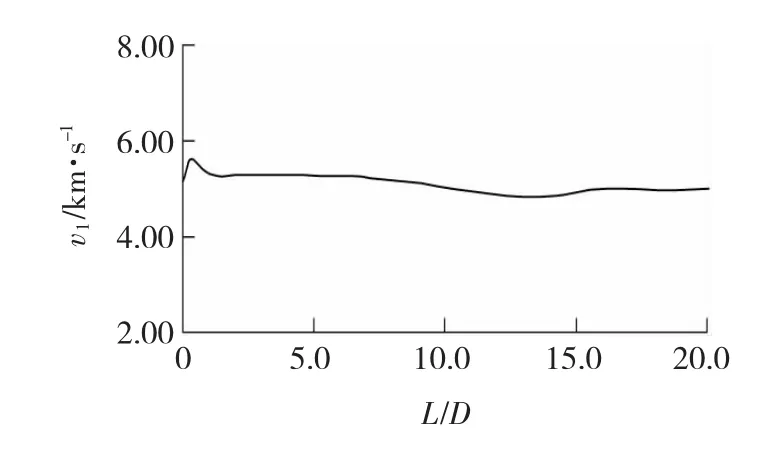
图4 碎片云前端轴向速度Fig.4 Tip particle axial velocity of debris clouds

为了考察弹丸长径比对薄板损伤程度的影响，文中给出了薄板穿孔直径随弹丸长径比的变化曲线，如图5所示，其中，D2为碎片云穿孔直径。由图5可见，不同长径比的圆柱形弹丸撞击薄板产生的穿孔直径随着弹丸长径比的增加而减小，即当弹丸的质量、撞击速度相同时，随着弹丸长径比的增加，弹丸对薄板的损伤能力减弱。

图5 薄板穿孔直径曲线Fig.5 Curve graph of hole diameters of thin plates

2.2.2 弹丸参考点速度

为了分析不同长径比的圆柱形弹丸撞击单层薄铝板后的破碎情况及速度特性，基于前述模型，在圆柱形弹丸上设置了四个参考点，参考点设置位置见图1。其中，参考点1、2位于弹丸前端表面，参考点3、4位于弹丸后端表面，且参考点2、4位于弹丸撞击轴上，参考点1、3位于弹丸外侧表面。

图6a给出了四个参考点轴向速度(va)随弹丸长径比的变化曲线。由图6a可以看出，当弹丸长径比L/D≥3.0，即撞击后弹丸有剩余长度时，随着弹丸长径比的增加，2～4参考点的轴向速度均保持在4.9 km/s左右，曲线近似为直线，即当弹丸长径比L/D≥3.0时，弹丸长径比对碎片云轴向速度影响不大。对于位于弹丸后表面的参考点3、4而言，在长径比L/D≥3.0时弹丸未发生破碎，仍沿着撞击轴方向运动，因此，轴向速度随弹丸长径比变化不大。参考点2位于撞击轴上，弹丸长径比对其轴向速度影响不大。在弹丸长径比介于0.1～3.0之间时，参考点3、4的轴向速度随弹丸长径比增加而增加，参考点2的轴向速度随弹丸长径比的增加先增加后减小。对于参考点1，弹丸材料在撞击过程中均会发生反溅，与弹丸长径比无关，且参考点1的轴向速度随着弹丸长径比的增加反溅速度减小。

图6b给出了四个参考点径向速度(vr)随弹丸长径比的变化曲线。由图6b可见，位于弹丸撞击轴上的参考点2、4，径向速度不随弹丸长径比变化而变化，始终在±0 km/s附近，即参考点2、4始终保持在撞击轴上;位于弹丸后表面的参考点3，纵向速度在弹丸长径比L/D＜1.4时随着长径比的增大而减小，当弹丸长径比L/D＞1.4时，弹丸长径比对碎片云径向速度影响不大，速度在±0 km/s附近，即当弹丸长径比L/D＞1.4时，参考点3位于撞击轴附近。参考点1的纵向速度随弹丸长径比变化不大，纵向速度维持在1 km/s左右。

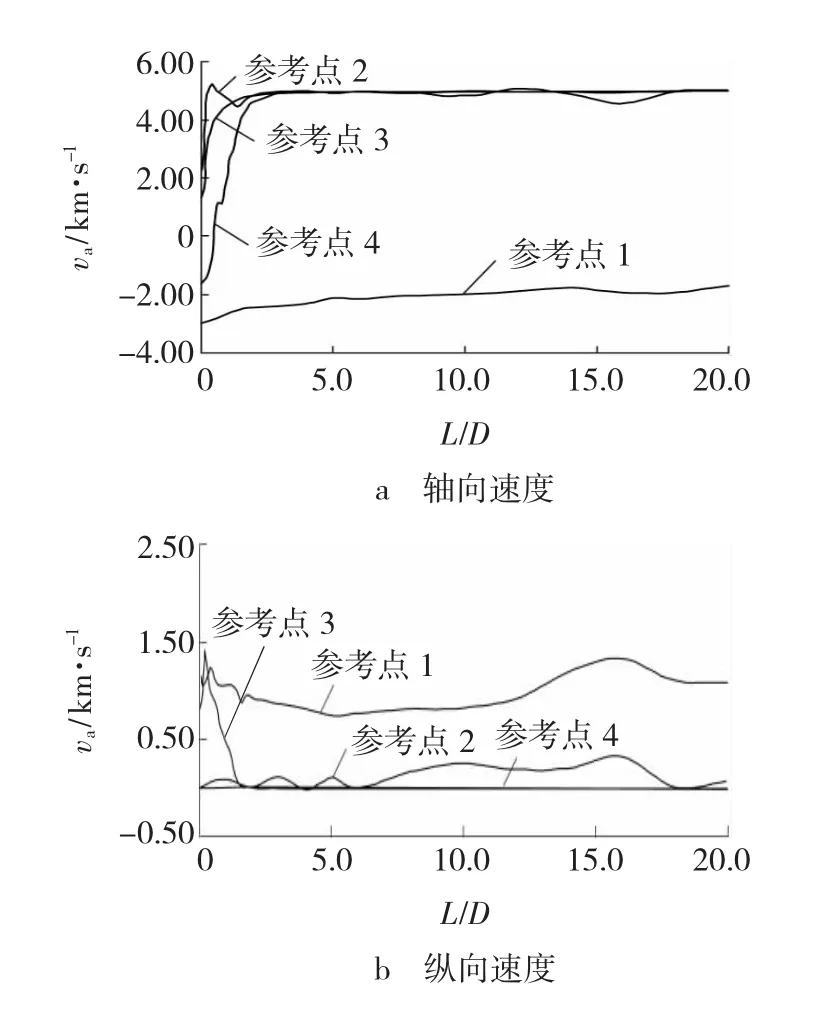
图6 弹丸参考点速度随长径比变化曲线Fig.6 Curves of reference point velocity with different ratio between length and radius

综合四个参考点轴向速度、纵向速度的分析结果可知，位于撞击轴上参考点2、4的轴向速度为4.9 km/s左右，纵向速度在±0 km/s附近，可以得出，位于撞击轴上的弹丸碎片撞击后仍在撞击轴上运动。当弹丸长径比L/D＞1.4时，参考点3的纵向速度在±0 km/s附近，即当弹丸长径比L/D＞1.4时，位于弹丸后表面的材料在撞击后运动方向与弹丸撞击方向相同。该结论与图1中当弹丸长径比L/D＞1.4时，碎片云中弹丸的大部分材料集中在撞击轴上的分析相符。位于参考点1附近的弹丸，在该文研究范围内，撞击过程中均发生反溅。

3 结论

应用AUTODYN－2D软件，采用SPH方法对圆柱形弹丸撞击防护屏产生的碎片云特性进行数值模拟研究。在弹丸的质量、撞击速度相同的情况下，分析圆柱形弹丸长径比对碎片云形态、运动参量的影响，所得结论如下:

(1)弹丸长径比越大，碎片云质量越集中;当弹丸长径比L/D≥3.0时，撞击后弹丸有剩余长度，且随着弹丸长径比的增加，弹丸剩余长度增加。

(2)随着弹丸长径比的增加，碎片云前端动能增大，对航天器舱壁的损伤能力增强，而弹丸对薄板的损伤能力减弱。

(3)位于撞击轴上的弹丸撞击后仍在撞击轴上运动。在该文研究范围内，位于弹丸前表面外侧的材料在撞击过程中将发生反溅。

[1]SMIRNOV N N，KISELEV A B，KONDRATYEV K A，et al.Impact of debris particles on space structures modeling[J].Acta Astronautica，2010，67(3/4):333－343.

[2]张 伟，庞宝君，张泽华.航天器微流星体及空间碎片防护结构性能分析[J].哈尔滨工业大学学报，2002，34(5):603－606.

[3]GRAHAM G A，KEARSLEY A T，GRADY M M.Natural and simulated hypervelocity impacts into solar cells[J].International Journal of Impact Engineering，1999，23(1):319－330.

[4]SCHARFER F K，HERRWERTH M，HIERMAIER S J，et al.Shape effects in hypervelocity impact on semi-infinite metallic targets[J].International Journal of Impact Engineering，2001，26(1):699－711.

[5]HU K F，SCHONBERG W P.Ballistic limit curves for non-spherical projectiles impacting dual wall spacecraft systems[J].International Journal of Impact Engineering，2003，29(1－10):345－355.

[6]WILLIAMSEN J E，EVANS S W.Predicting orbital debris shape and orientation effects on spacecraft shield ballistic limits based on characteristic length[J].International Journal of Impact Engineering，2006，33(1－12):862－871.

[7]徐 英，时家明，林志丹.撞击物形状和速度对高速撞击结果的影响[J].弹箭与制导学报，2010，30(2):106－110.

[8]盖芳芳，于丽艳，于月民.非球形弹丸超高速撞击充气压力容器碎片云特性数值模拟[J].黑龙江科技学院学报，2013，23(3):231－235.

[9]贾光辉，黄 海，胡震东.超高速撞击数值仿真结果分析[J].爆炸与冲击，2005，25(1):47－53.

[10]徐金中.基于SPH方法的空间碎片超高速碰撞特性及其防护结构设计研究[D].长沙:国防科学技术大学，2008:55－65.

[11]CORVONATO E，DESTEFANIS R，FARAUD M.Integral model for the description of the debris cloud structure and impact[J].International Journal of Impact Engineering，2001，26(1－10):115－128.