深部巷道围岩蠕变的数值模拟

张周鑫,　刘丽红

(安徽理工大学 地球与环境学院, 安徽 淮南 232001)



深部巷道围岩蠕变的数值模拟

张周鑫,刘丽红

(安徽理工大学 地球与环境学院, 安徽 淮南 232001)

煤矿深部开采时,针对高地应力下岩体蠕变导致的巷道围岩变形问题,分析了围岩变形破坏特征,并结合现场相关地质资料,采用FLAC3D程序的Burgers蠕变模块,对不同围压条件下巷道围岩蠕变问题进行模拟研究。结果表明:围岩的蠕变存在着初始蠕变和稳定蠕变两个阶段；围岩的蠕变移近量、变形速率和应力均随时间的延长而增大,最终趋于稳定。该研究对高地应力条件下巷道施工有一定指导意义。

巷道; 高地应力; 围岩蠕变; 数值模拟; FALC3D

(School of Earth & Environment, Anhui University of Science & Technology, Huainan 232001, China)

0　引　言

随着浅部煤炭资源的逐渐萎缩,向深部开采的力度与需求在不断地加大。大量工程实践表明,深部硐室、巷道开挖后,在外界荷载的长期作用下围岩的应力-应变状态及破坏形态都会随时间的变化而不断改变,从而表现出明显的时效特征和流变特性。天然岩体属于不连续、非均质、各向异性的力学介质,大量的流变实验研究表明,在单轴应力条件下当岩体所处的应力水平较低时,岩石就会呈现出类似固体材料的黏弹性变形特征;一旦加载应力超过岩体应力阀值,则会出现类似流体材料的黏塑性变形特征。近年来,煤矿的深部开采使巷道的安全稳定性问题逐渐显现,而这又与岩石的流变力学特性密切相关。目前,国内关于围岩蠕变的理论研究成果较为丰富[1-6],其中,王永岩等[7]对深部工程中不同深度的巷道围岩在高地应力作用下的蠕变破坏过程进行了数值模拟,得到了时间-蠕变、水平地应力-蠕变曲线组和时间-水平地应力-蠕变三维曲面, 应用Mohr-Coulomb和Griffith破坏准则,获得了高地应力岩体的非线性蠕变破坏的规律。但深部巷道围岩流变特性的研究还较少,因此,文中应用FLAC3D数值模拟软件中的Burgers蠕变模型,模拟分析不同围压条件下,围岩的应力、形变、位移速率随时间的变化关系;同时,从流变的角度,运用力学理论,对高地应力下巷道围岩蠕变特性进行分析研究。

1　数值模型

1.1研究背景

谢一矿谢李大井服务于-660 m以下深部水平,以综采综掘为主,为深井开采实验矿井。文中数值模型以此为工程背景,设计尺寸60 m×100 m×60 m,巷道半圆部分半径为2 m,侧帮高2 m,巷道置于单一岩层中,顶底岩层简单化处理为岩组;模型施加水平约束,底界垂直约束,顶界面据不同深度h分别设置不同压力。为较好反应不同围压条件下巷道蠕变特征,结合矿井实际,拟定-660、-960和-1 200 m三个水平为具体研究对象。

1.2模型选取

FLAC3D软件在解决非线性大变形问题上具有很大的优势,其中的蠕变本构模型共有八个,该次模

拟选取能很好的描述这种煤岩蠕变规律的Burgers蠕变模型[8-12]。该模型是由一个开尔文模型和一个马克斯威尔模型串联而成的,其中马克斯威尔模型具有瞬时蠕变、稳态蠕变和非线性松弛,且具有黏性流动的特征;开尔文模型具有衰减蠕变和弹性后效的特征。模型的具体表达式为

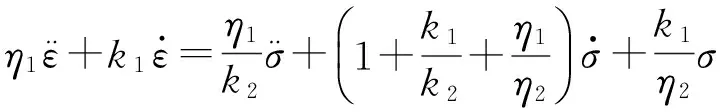
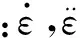
k——刚度系数;

η——黏度系数。

Burgers模型如图1所示,图1a为本构模型,图1b为蠕变移近量随时间变化关系,图1c为当应力值一定时形变量与时间的关系。

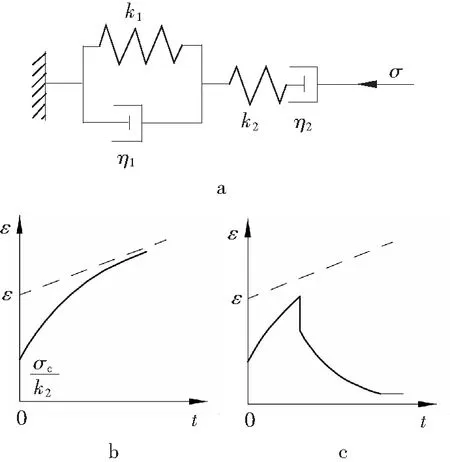
图1　Burgers模型Fig. 1　Burgers model

1.3参数确定

根据相关资料建立模型,所需的各参数见表1,计算模型及初始最大主应力平衡如图2、3所示。

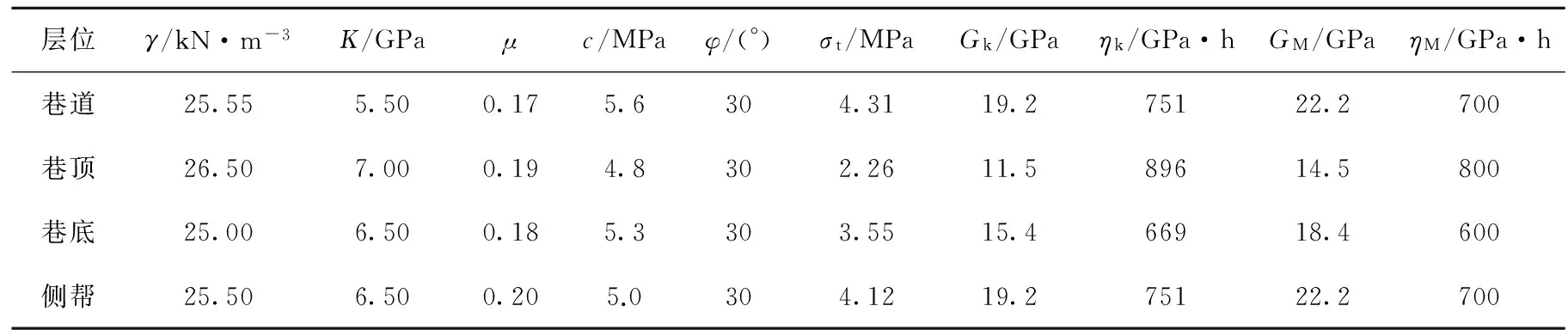
表1　模型参数Table 1　Parameters of model

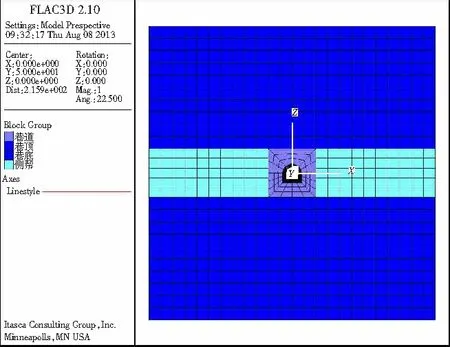
图2　计算模型Fig. 2　Calculation model

图3　最大主应力平衡Fig. 3　Map of max main stress balance

2　结果与分析

由于蠕变计算与动力计算不能耦合,因此计算过程中先用蠕变计算应力场,然后进行瞬态的动力计算。蠕变过程由偏应力状态控制,从数值计算的精度来讲,最大蠕变时间步长可以表示成材料黏性常数和剪切模量的比值。计算过程自动调整时间步长, 同时在计算的过程中设置检测点对蠕变移近量及速度进行采样。

设置巷道蠕变时间为20 a,导出巷道检测点形变图表,分析无支护巷道的蠕变特性。由图4可知,无支护巷道围岩在不同的围压条件下，在开始的250 d左右处于初始蠕变阶段,随后有一个较短时间的过度阶段,270 d之后进入稳定蠕变阶段。由于围压的不同,围岩蠕变移近量也表现出不同的曲线特性,如图4所示,随着深度的增加,形变量的变化率越大,越能更好地反应围压大小对岩石蠕变的影响。

图5为相同检测点围岩蠕变速度曲线,总体趋势是在蠕变时间为250 d内围岩变形速率相差很大,在某一时刻达到了峰值速率,呈现出类抛物线特征;随后经历一段时间的波动,最终分别达到稳定变形速率的状态。同时,在巷顶及侧帮的速率检测结果表明,由于深度的影响,变形速率的峰值与稳定状态值也呈对应关系。

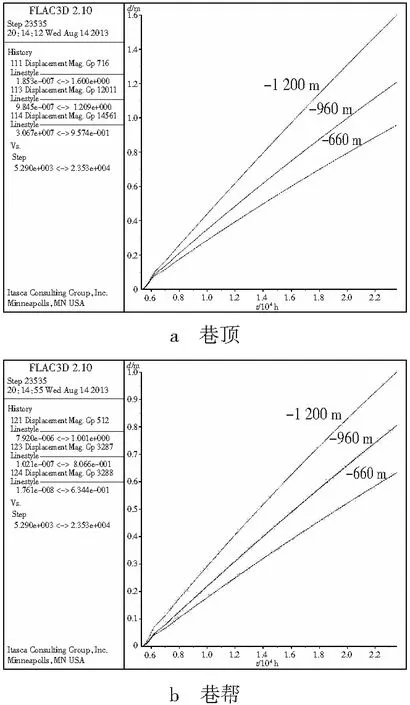
图4　岩石形变时程曲线Fig. 4　Time-histories curve of deformation in roadway rock

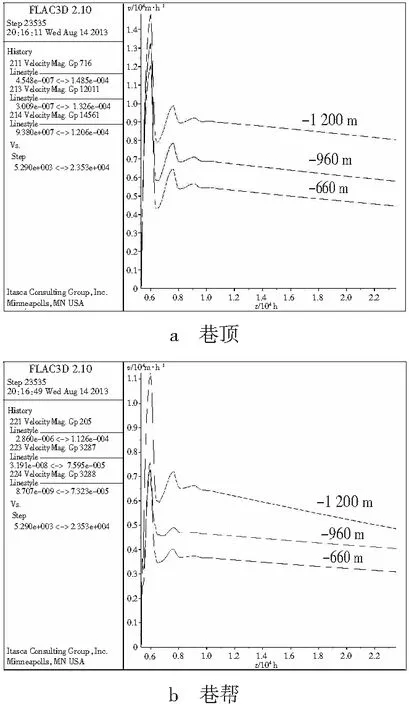
图5　岩石蠕变速率曲线Fig. 5　Velocity curve of rocks creep

图6a为巷道深度是-660 m时的垂直应力云图,由图6a可知,巷道中心及附近位置应力最小为1 MPa,两帮位置最高达10 MPa,且在模型范围内拉、压应力同时存在;应力的总体形态呈现出以巷道中心为轴对称的均匀分布,顶底板范围内表现出应力拱型特征。当深度增加到-960 m时,巷道围压增大,围岩垂直应力云图的形态特征略微发生变化,在巷道两帮外围小范围内应力集中达到最大的压应力,形态几乎呈对称均匀分布,巷道横向5 m范围内为拉应力区,应力最小(图6b)。当巷道深为-1 200 m时,受深部地应力影响,模型全局范围内受压应力作用,且在巷道侧帮横向上达到最大,顶底板应力近乎梯度变化(图6c)。

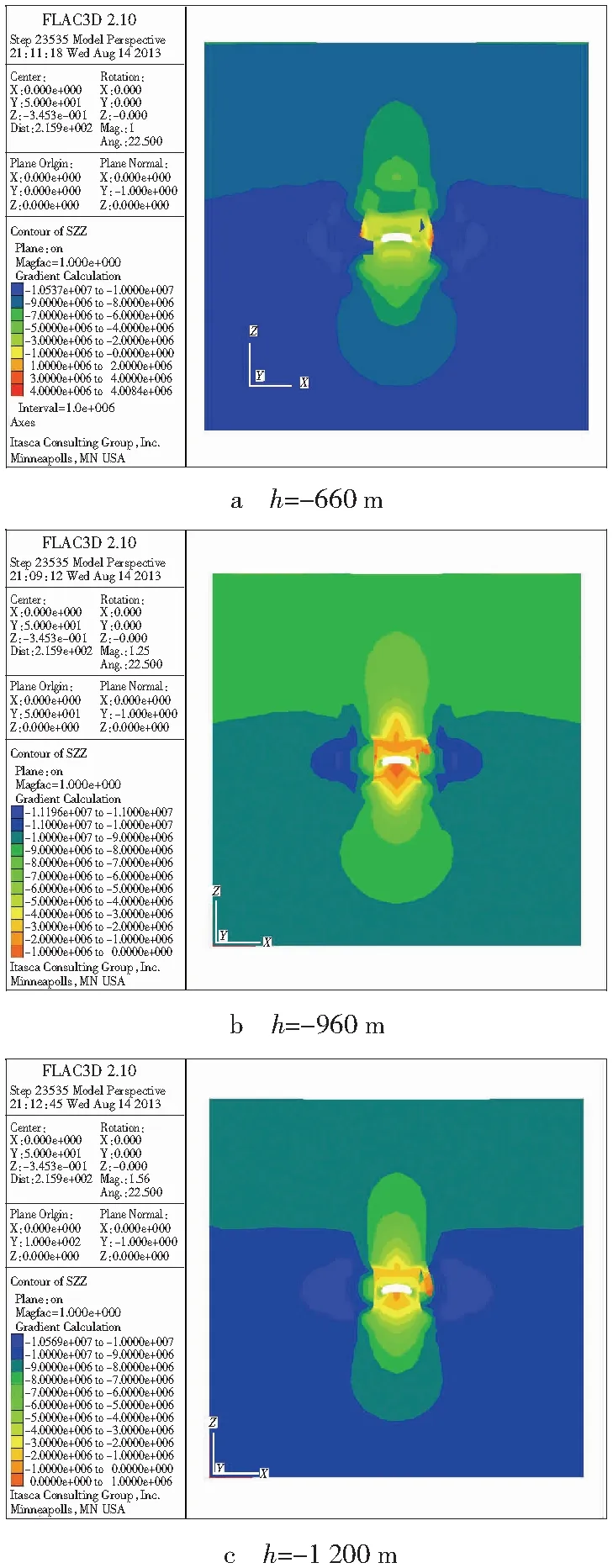
图6　不同深度围岩蠕变垂直应力云图Fig. 6　Vertical stress nephogram of surrounding rock under different depth

3　结　论

(1)运用FLAC3D软件蠕变模块分析了不同围压条件下,无支护巷道的蠕变特性,得到了不同深度巷道围岩的形变量、变形速率及应力变化特征图,并分析了巷道蠕变的应力场分布规律,描绘了巷道顶板及两帮的蠕变位移曲线和变形速率曲线,清晰地反应出围岩蠕变的应力、应变随时间变化的流变特征。

(2)不同深度的巷道围岩蠕变表现出相似的特征,均分为初始蠕变和稳态蠕变两个阶段,且随着深度增加蠕变量增大且加快;进入到稳态蠕变之后表现出几乎线性的黏弹性特征。

(3)确定具体条件下蠕变的时间历程,在相应阶段采取措施,可在一定程度上控制巷道围岩变形。

[1]李大伟, 侯朝炯. 围岩应变软化巷道锚杆支护作用的计算[J]. 采矿与安全工程学报, 2008, 25(1): 123-126.

[2]薛琳. 巷道围岩支护系统黏弹性分析蠕变柔量法[J]. 煤炭学报, 1996, 21(6): 591-595.

[3]王祥秋, 杨林德, 高文华. 软弱围岩蠕变损伤机理及合理支护时间的反演分析[J]. 岩石力学与工程学报, 2004, 23(5): 793-796.

[4]华心祝, 吕凡任. 锚注软岩巷道流变研究[J]. 岩石力学与工程学报, 2003, 22(2): 297-303.

[5]张源, 万志军, 李付臣， 等. 不稳定覆岩下沿空掘巷围岩大变形机理[J]. 采矿与安全工程学报, 2012, 29(4): 451-458.[6]刘夕才. 软岩巷道的粘弹性流变分析[J].矿山压力与顶板管理, 1997(1): 29-31.

[7]王永岩, 李媛. 软岩流变模型实验相似准则的推演及应用[J]. 辽宁工程技术大学学报:自然科学版, 2012, 31(3): 354-357.[8]张向东, 郑雨天, 吕兴亚, 等. 软弱岩体Berger 模型及井巷流变地压[J]. 中国有色金属学报, 1997, 7(1): 13-17.

[9]刘栋. 深部围岩蠕变特性试验研究[D]. 长沙: 湖南科技大学, 2011.

[10]韩猛, 王连国. 巷道围岩蠕变特性及支护效果数值模拟研究[J]. 矿业工程, 2011, 9(4): 61-64.

[11]邵祥泽, 潘志存, 张培森. 高地应力巷道围岩的蠕变数值模拟[J]. 采矿与安全工程学报, 2006, 23(2): 245-248.

[12]王东, 董正筑, 张爱萍, 等. 软岩巷道围岩指数蠕变模型流变分析[J]. 合肥工业大学学报:自然科学版, 2007, 30(11): 1485-1488.

(编辑王冬)

Numerical simulation on creep for surrounding rocks of deep laneway

ZHANGZhouxin,LIULihong

Aimed at addressing the deformation of the surrounding rock of roadway triggered by the creep of rock mass subjected to high in-situ stress, such as occurs in deep coalmining, this paper describes an analysis of the distortion and failure character of surrounding rock and a simulation on the creep of tunnel surrounding rock under the different confining pressure, combined with related field geological data and using the burgers creep module of FLAC3D. The results show that rock deformation around roadway, deformation rate, and stress increase with time and tend to be stable. The creep involves two stages: initial creep and steady creep. This research is of a certain guiding significance for the construction of roadway under the high in-situ stress.

mining roadway; high stress; surrounding rocks creep; numerical simulation; FLAC3D

2013-09-17

国家自然科学基金项目(41201017)

张周鑫(1988-),男,安徽省安庆人,硕士,研究方向:水文地质与工程地质,E-mail:zhxzhang88@163.com。

10.3969/j.issn.1671-0118.2013.06.004

TD315.3

1671-0118(2013)06-0519-04

A