一种改进的离焦模型
王婧林, 李俊山
(第二炮兵工程大学 信息工程系,西安 710025)
0 引言
随着科学技术的迅速发展,各种成像传感器的应用正在迅速增加。数字图像处理技术也进入了应用的新时代,如图像增强、复原、压缩与识别等。尽管许多成像系统可以实现自动聚焦,但离焦模糊现象仍然存在[1]。离焦现象是一种由摄像机和物体的相对运动造成的常见图像退化现象。对离焦模糊图像的复原技术一直是国内外图像处理领域的重要研究内容[2]。
常用成像系统的离焦模型描述离焦现象。典型离焦模型由点扩散函数及其参数组成。点扩散函数描述输入物为一点光源时其输出像的光场分布。对于理想的成像系统,点扩散函数通常可描述为将物空间中的一点映射于成像空间中的一点。但当图像发生离焦现象时,该物空间中的一点将映射于像空间中的具有不同光强的点集。
典型的离焦图像复原方法是选择离焦模型(如圆盘离焦模型)并在图像的变换域(如频域)内寻找零点位置确定模型参数,后通过逆变换获得清晰图像[3-5]。该方法需要手动选择离焦模型,因此难以在自动图像处理系统和批量图像处理系统中应用。为了解决该问题,笔者提出一种改进的离焦模型,该模型根据离焦图像的圆对称性估算离焦的点扩散函数及其参数。
1 技术背景
首先回顾图像退化模型。成像区域内对象的不同深度将导致产生离焦图像。目前,常用于描述该现象的退化模型如图1所示。图1中g(x,y)是退化图像,f(x,y)是原始图像,h(x,y)是成像系统的点扩散函数,n(x,y)是加性噪声。添加的噪声影响原始图像,并在某些情况下,产生退化图像。而图像复原是图像退化的逆过程[6]。
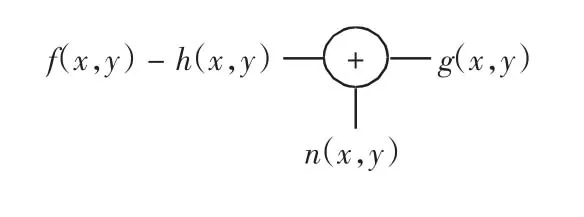
图1 图像退化模型Fig.1 Degradation model
如果成像系统是不变的线性移动,退化过程可表示为式(1):
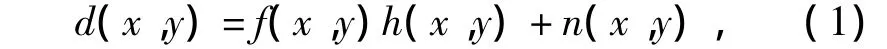
相应的频域表达式如式(2)所示:
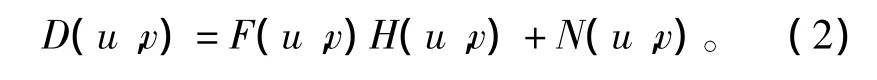
由上述分析可知,根据离焦模型,通过逆变换离焦图像即可实现图像复原,其关键是如何确定离焦模型,即点退化函数及其参数。下面分析典型的离焦模型及其点退化函数,即圆盘离焦模型和高斯离焦模型。
1.1 经典圆盘离焦模型
经典圆盘离焦模型源于几何光学关于离焦图像方面的研究。几何光学表明:物空间中的一点通过理想成像系统后在图像空间中将形成与之对应的像点,然而,当现实中由物面、镜面或成像平面造成的距离不满足高斯成像公式时,该像点实际将形成一圆盘[3]。该过程的原理如图2所示。其点扩散函数可以近似为圆盘函数:

式中,需要求解的模糊半径r是唯一的未知参数。半径确定后,能够在频域内得到退化函数的表达式。然后,通过相应的滤波器可以导出原始图像的频域表达式,并且通过逆傅里叶变换实现图像复原。
为确定模糊半径r,对式(3)所给的退化模型进行傅里叶变换,得到:
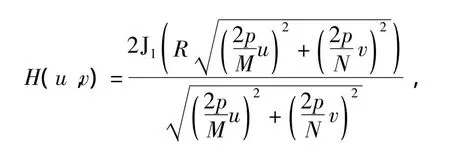
式中,J1(·)为一阶第一类Bessel函数,且二维傅里叶变换的尺寸为M×N。根据一阶第一类Bessel函数的性质可知H(u,v)位于频域的第一个暗环中,第一个零点的轨迹如式(4)所示:
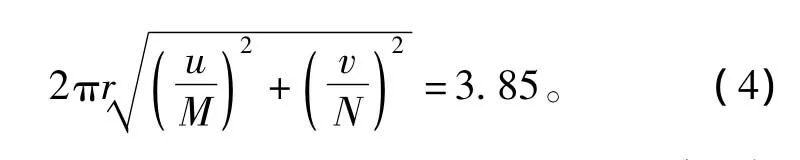
对于一个相对较小的噪声,通过式(4)可知:如果找到u,v是对应于离焦模糊图像傅里叶变换的第一个零(暗环),那么r可以通过式(4)求得。

图2 圆盘离焦模型原理Fig.2 Schematic of disk defocus
1.2 高斯积分离焦模型
高斯积分离焦模型与圆盘离焦模型间有差异。它不是来源于光学知识,而是通过考虑各种因素得到的一个近似模型,高斯积分离焦模型的原理如图 3所示[3]。
相应公式可表达为
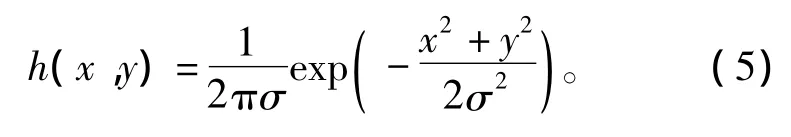
在式(5)中,模糊半径σ是唯一的未知参数,其决定于离焦模糊图像。进而可以通过滤波得到离焦复原。通过离焦模糊图像的零焦点求得参数的方法不适合高斯模型。它可以通过空间域边缘函数曲线的检测而得到。从式(5)的积分公式可知,线扩散函数仍然服从高斯分布,如式(6)所示
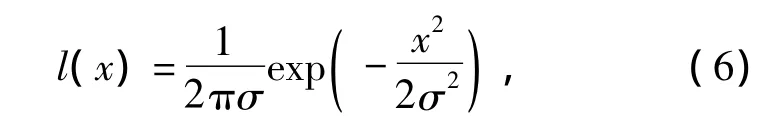
同时,从式(5)的积分公式可获得边缘函数:
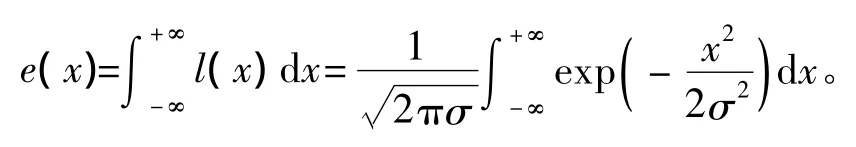
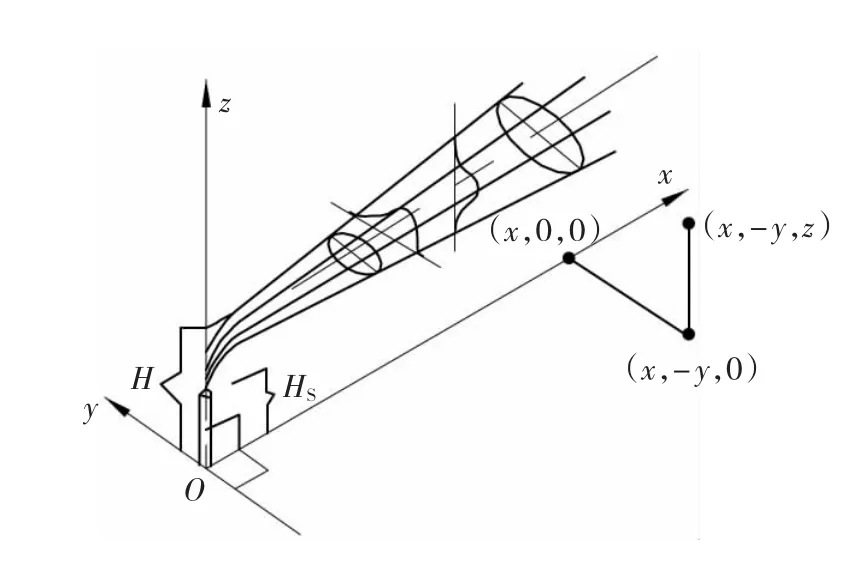
图3 高斯离焦模型Fig.3 Schematic of Gaussian defocus
2 离焦模型的改进
认知心理学实验表明,人的肉眼对边缘的反应比对点和线的反应更敏感;同时,边缘在成像系统中直边物体的反应也很容易获得;基于上述原因,文中通过对直边物体的反应得到线扩散函数。然而,将线扩散函数用于任意成像系统是困难的。因为,任意系统在像空间内不同方向上的线扩散函数不尽相同,即线扩散函数不能完全反映所有系统的特征,而需要从不同方向衡量其有效性。但当系统为圆对称时,即在像空间内各方向均对称时,线扩散函数可完全描述系统特征[7]。文中研究通过线扩散函数作为描述圆对称系统的离焦模型函数。
如前所述,对于圆系统中的逆阿贝尔变换,任意方向的线扩散函数可以决定点扩散函数。假设,圆对称情况下的点扩散函数h(x,y)具有如下形式:
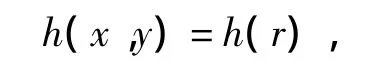
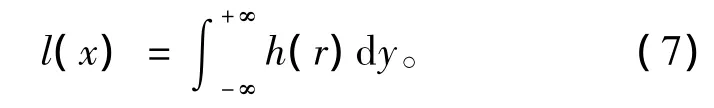
相反,利用线扩散函数的点扩散函数,可以定义边缘函数
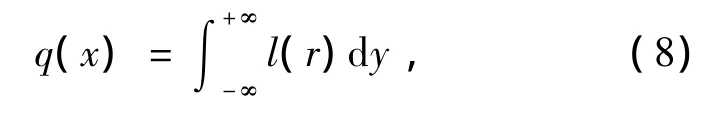
则点扩散函数:
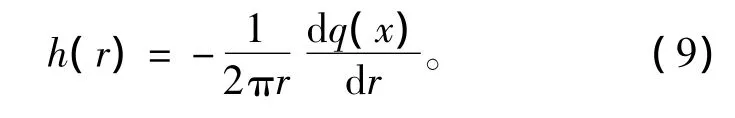
合并方程(8)和(9)可以得到
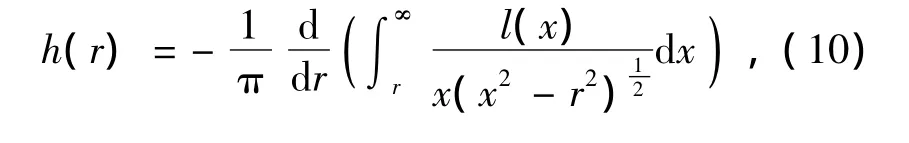
式(10)表示的是逆阿贝尔变换。将式(10)带入式(7)可以得到阿贝尔变换
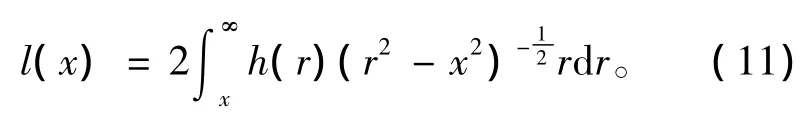
在计算过程中,积分的上限可设为模糊半径R(由于其圆对称性,在一个有限的圆形区域,h(x,y)可以非零)。
采用式(11)计算点扩散函数,需要估计系统的模糊半径R。一种可行的方法是通过高斯分布的点扩散函数近似估计模糊半径R。并由引人注目的高斯模型参数确定σ。而后,令R0=2σ为模糊半径的初始值,通过斐波纳契最优搜索法得知R的实际值接近于R0。
3 验证实验
为了验证方法的有效性,文中将提出的离焦模型应用于经典的离焦模糊图像复原算法中[3,6]。该算法以高斯分布点扩散函数近似估计模糊半径R,然后确定点扩散函数并进行离焦复原。文中将上述算法用于实际图片并与采用圆盘离焦模型和高斯离焦模型的算法所得结果进行比较,如图4所示。为了便于对比,各复原图片中的局部被原尺寸展示于图5。将复原图片与对应的清晰图片(图5a)对比可以发现,采用增强离焦模型的复原图像较采用圆盘模型和高斯模型的复原图像更加清晰。

图4 实验结果Fig.4 Experiment results

图5 局部图片Fig.5 Lccal image
4 结束语
当前研究常用离焦模型描述离焦模糊现象。离焦模型由点扩散函数及其参数组成。常用的离焦图像复原方法使用离焦模型逆变换获得清晰图像。为此,需要预先选择离焦模型,并通过分析离焦图像获得模型参数。文中分析对比了目前常见的离焦模型(圆盘模型和高斯模型),并针对这些模型往往不能准确描述离焦模糊现象的问题,提出一种改进的离焦模型。该模型根据离焦图像的圆对称性估算离焦的点扩散函数及其参数,从而准确描述离焦现象。该模型被应用于典型的离焦复原算法中,真实图像实验证明了该模型的有效性。
[1]吴振宇,杜少军,姚洪利.采用聚焦度量的散焦模糊图像参数鉴别及复原[J].红外与激光工程,2011,40(4):772-776.
[2]QIN FENGQING.Blind image restoration based on wiener filtering and defocus point spread function estimation[C]//2012 5thInternational Congress on Image and Signal Processing(CISP).Chongqing,China:IEEE,2012:360-363.
[3]章毓晋.图像处理和分析基础[M].北京:高等教学出版社,2011.
[4]曹茂永,孙农亮,郁道银.离焦模糊图像清晰度评价函数的研究[J].仪器仪表学报,2001,22(22):259-268.
[5]孙 辉,张 葆,刘晶红,等.离焦模糊图像的维纳滤波恢复[J].光学技术,2009,35(2):295-298.
[6]何志彪,张新访,朱光喜.离焦模糊图像增强技术的研究[J].红外与毫米波学报,2001,20(6):447-450.
[7]刘 昶,王 玲.基于小波的离焦模糊图像清晰度判定[J].计算机应用与软件,2008,25(7):239-240.

