月球探测器动力下降段最优轨迹参数化方法
乔衍迪,张泽旭,2,邓涵之,徐田来,2
(1.哈尔滨工业大学深空探测基础研究中心,哈尔滨 150001;2. 陕西省组合与智能导航重点实验室,西安 710000;3. 济南大学自动化与电气工程学院,济南 250022)
0 引 言
近年来,包括中美在内的多个国家组织均推出了自己的探月计划,月球探测重新成为深空探测任务的焦点。月球探测器软着陆过程主要分为动力下降段、姿态调整段和垂直下降段三个阶段,其中动力下降段要求探测器距离从距月面15 km下降到3 km,探测器的速度从1.7 km/s降至0附近,为保证后续姿态调整段具有充分的高度与速度余量,要求动力下降段的末制导具有高精度的速度和高度。但是,从月球轨道离轨进行霍曼转移,进入动力下降段容易出现高度控制偏差,本文充分考虑动力下降段的起始高度波动影响,提出一种高精度参数化制导方法,在燃料更省的基础上实现高精度动力下降段末制导。
随着航天技术的发展,对月球探测器实现自主高精度制导的需求更加迫切。月球软着陆制导方法主要分为三类:重力转弯制导法、标称轨道制导法和显式制导法,国内外对各种制导方法已经开展了多年深入的研究工作。重力转弯制导法原理简单,多出现在20世纪低成本探月任务设计中。标称轨迹法即设计一条着陆轨迹,探测器根据位置和速度信息跟踪理想轨迹实现软着陆。文献[1-2]将月球软着陆轨迹进行离散化,再利用序列二次规划方法(Sequential quadratic programming,SQP)进行数值求解。文献[3]针对软着陆与采样返回轨道进行B样条数值逼近,在复杂约束下得到了高精度着陆轨迹,但是标称轨迹法对于初始偏差敏感,不一定能够实现完美跟踪。显式制导法根据探测器的实时位置和速度信息,实时计算制导指令。文献[4-5]利用高斯-伪谱法实现了探测器二维定点软着陆轨道优化,求解了月面安全的着陆区范围。文献[6-8]对闭环软着陆轨迹跟踪算法进行了研究,有效地减小了制导误差,提高了制导系统的稳定性。文献[9]考虑到月球软着陆任务的工程实际,设计了可以实现机载计算机自主规划的月球软着陆显式制导律,该方法计算简单,可以快速规划出着陆轨迹。文献[10]提出了混合制导方法(Hybrid guidance law,HGL),但是该制导律只适用于软着陆姿态调整段,以实现目标着陆点的重决策;近年来随着最优问题的研究深入,更多的数学规划方法被应用到时深空探测领域。文献[11-12]运用凸优化理论解决月球软着陆问题常出现的局部无解问题,得到的最终着陆高度误差约200 m。文献[13]将状态和控制变量进行参数化,结合迭代的方法,解决了非线性系统最优控制问题。文献[14-16]结合了控制变量参数化方法和强化技术,并成功应用于月球软着陆轨迹的优化问题,但构建的动力学参数复杂,控制变量较多,不适合运用探测器的机载计算机解算,且需要用到专业的数学软件,实用性较差。本文综合考虑月球探测器软着陆动力下降段的快速性和工程实用性,简化控制变量,提出了一种改进的燃料最优的显式制导律,并利用控制变量参数化方法,快速规划着陆轨迹,引入时间尺度变换方法,求解得到了软着陆动力下降段最优着陆轨迹。
1 软着陆动力学模型
月球探测器软着陆动力下降段中,探测器从15 km的椭圆轨道下降至月球表面3 km处,且横向行程较长,但是历时较短,因此可以将月球视为均匀球体,忽略月球自转,建立三维软着陆模型[17]。
用U,V,W表示探测器在探测器着陆坐标系中的速度分量,有:
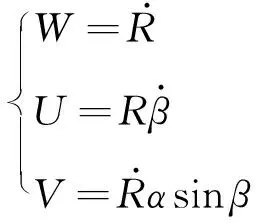
(1)
式中:α和β为着陆坐标系的方位角和仰角,R为探测器与月心的距离。在不考虑摄动影响且忽略月球自转情况下,得到月球探测器动力下降段的动力学模型,有:
(2)
式中:μ为月心引力常数,F为探测器制动发动机推力且为常数,Φ为探测器推力仰角,Θ为推力的推力倾角,Isp为制动发动机的比冲,gE为地球重力加速度,m为探测器的总质量。
探测器软着陆过程动力下降段的初始位置和初始速度可写为:
(3)
动力下降阶段的终端约束条件除了速度分量约束外,还包括高度约束:
(4)
2 月球探测器软着陆燃料最优轨道求解
2.1 最优控制问题
利用最优控制方法直接求解月球探测器软着陆问题比较复杂,动力学模型具有较强的非线性,且难以获得解析形式的表达式。通常需要利用给定初值进行迭代的方法求解,不利于在飞行器上实现自主控制。因此,需要对软着陆模型进行简化。
引入两个假设:1)假设月球表面为平面,引力场均匀,且月球引力加速度为常数,则月心惯性坐标系和探测器着陆坐标系Oxoyozo的瞬时坐标轴一致,用u,v,w表示探测器的速度分量;2)假设探测器采用变推力发动机,即制动加速度不随着探测器的质量发生变化,是常值。
基于假设,式(1)所表示的动力学模型可简化为:
(5)
式中:aN表示探测器推力F与质量m的比值,gm为月球的引力加速度,θ为简化后探测器推力仰角,φ为推力倾角。
探测器在动力下降段需要消耗大量的燃料抵消初始速度,因此应将燃料作为最优控制问题的性能指标。对于动力下降段的连续制动控制,燃料最优目标函数:

(6)
寻求最优控制变量u*=[θ*,φ*]T,使得探测器在短时间由式(3)的初始状态完成动力下降过程,并满足式(4)的终端约束。与之对应的状态变量[x*,y*,z*]T即为动力下降段的最优着陆轨迹。
对于月球探测器软着陆动力下降段的最优控制问题,通常根据状态变量和控制变量的初值,猜测协状态变量或中间变量,利用迭代的方法对当前状态进行优化,即将剩余时间tgo划分出多个时间节点,分段进行控制变量u*=[θ*,φ*]T的优化,状态变量不断更迭,直到满足终值约束。
2.2 改进的制导律设计
结合月球探测器软着陆的动力下降段特点:经过霍夫曼转移,探测器在xoOozo平面内水平初始速度远大于另外两个方向的初始速度。因此,制动发动机的主要工作是抵消水平初始速度u0,则对于控制变量u=[θ,φ]T,推力倾角φ≈180°,并将推力仰角θ视为小量。
利用庞得里亚金极大值原理,可以得到Hamiltonian方程:
H=1+λuaNcosθcosφ+λvaNcosθsinφ+
λw(aNsinθ-gm)+λxu+λyv+λzw+
(7)
式中:λi(i=u,v,w,x,y,z)为共轭变量,且满足:
(8)
则最优解为:
(9)
(10)
简化为:
(11)
tanθ≈sinθ=κ1+κ2t
(12)
式(5)的探测器动力学方程可以写作:
(13)
求解两点边值问题,得到ψ0、κ1、κ2和tgo。
(14)
则月球探测器软着陆的动力下降段的历时tgo为:
(15)
改进的显式制导律在探测器软着陆过程中无需解算协状态变量,根据当前的速度解算得到推力仰角,探测器高度的表达式为三次多项式,通过多步迭代可以获得探测器的最优燃料制导律的着陆轨迹。
3 控制变量参数化方法求解着陆轨迹
3.1 控制变量参数化
上节中,根据庞得里亚金极大值原理将月球软着陆转化为两点边值问题求解,但由于协状态变量的初值没有物理意义,迭代计算引入了积分问题,计算量较大。因此,本节采用控制变量参数化(CVP)方法,将月球软着陆轨道离散化,分段求解最优控制问题。
本文将采用基于标称轨迹的离散化方法解决分段最优控制问题,月球软着陆最优制导问题转化为含有一般约束的数学规划问题,通过内点法求解[18]。
(16)
对于式(16),寻找控制变量u,使目标函数:
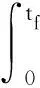
(17)
最小,Φ0(t,x(t),u(t))其中为终端性能指标,L0(t,x(t),u(t))为积分性能指标。
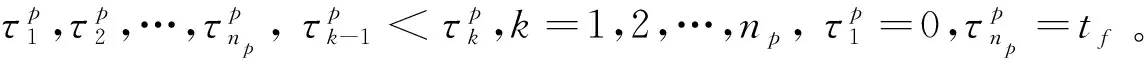
(18)

3.2 时间尺度变换
若时间序列不固定那么求取参数的梯度信息变得很困难[20]。为此,引入时间尺度变换法,假设新的时间变量s∈[0,1],将不确定的下降时间t1重定义到s∈[0,1]中:
(19)
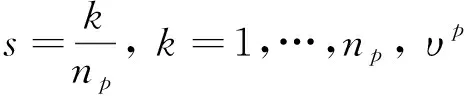
(20)
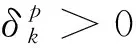
(21)
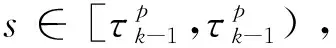
t1(1)=tf
t1(0)=0
定义:
wp(s)=up(t1(s))
则
(22)
将时间尺度变换式(16)代入非线性系统中:
δp,σp)υp(s)
(23)
及
(24)
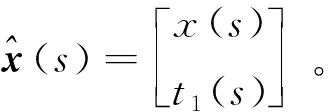
由于软着陆任务动力下降段的主要任务是抵消探测器较大的水平速度,使其在姿态调整段的初始速度接近于0,且下降高度不低于3 km,将速度u,w与月心距r作为路径约束。最优控制问题的目标函数写作:
(25)
由此,转换状态约束进入目标函数中,采用变分法给出系统(16)梯度信息,定义变分系统如下:
(26)
则一阶梯度信息可以通过下式得到:
(27)
由此采用变分法,可以求解状态方程组,具有较好的数值稳定性和较高的精度,所需求解的微分方程不多,不会给求解带来负担。先给出梯度信息与终端约束之差ε的值,检验是否符合约束条件,若不符合,重新规划控制变量参数的取值范围。显然,对于每条轨迹一定能够找到足够小的取值范围使约束条件满足,当减小到给定值时这个计算过程就停止。很明显,当误差足够小时,能够达到满足要求的近似。误差定为ε≤10-3。
下面给出基于标称轨迹的控制变量参数化算法具体的实现流程图,如图1所示。
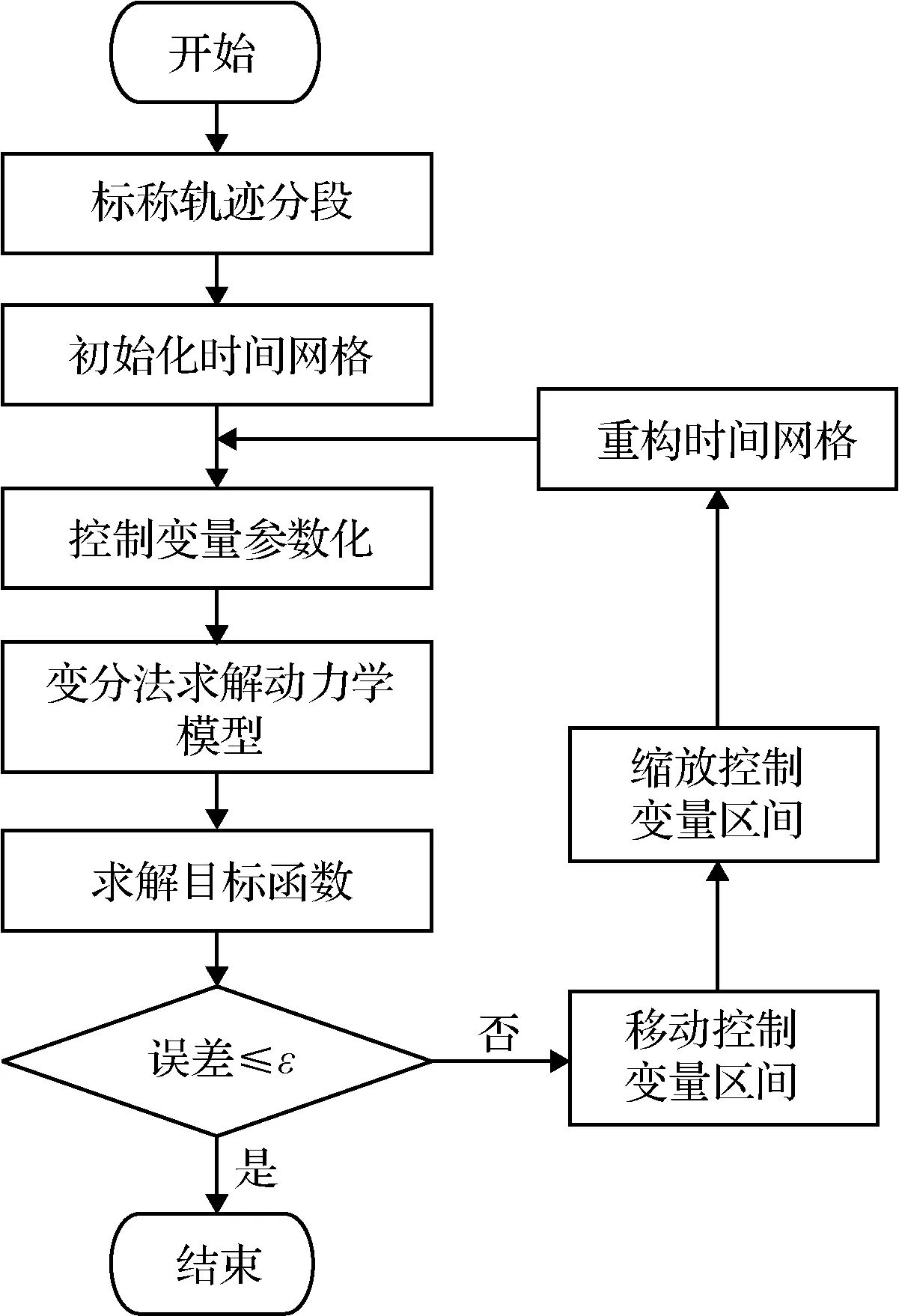
图1 基于标称轨迹的控制变量参数化算法流程图Fig.1 Flow chart of trajectory generation algorithm based on control variable parameterization method
4 仿真校验
月球探测器的初始质量m0=750 kg;制动发动机的最大推力为Fmax=1750 N,比冲为Isp=316 s;初始水平速度为U0=1692 m/s,其它两个方向初始速度分量为W0=V0=0。月球引力常数μ=4.903×1012m3/s2,近月点与月心距离R0=1753 km,最终着陆点与月球表面的距离为RF=1741.03 km,最终着陆速度约束分别为|Uf|≤1 m/s,|Wf|≤1.5 m/s,|Vf|≤3.8 m/s,由改进的多项式制导方法得到的着陆时间为607.956 s,利用CVP方法得到的最终着陆时间为605.85 s,减少了2.1 s。
如图2所示,动力下降段结束时,由改进的多项式制导律得到的探测器的最终质量为396.94 kg,由CVP算法得到的最终质量为398.69 kg,燃料少消耗了1.75 kg。

图2 质量变化曲线Fig.2 The mass curve
如图3所示,月球探测器在动力下降段结束时三轴速度分别为Uf=0.309 m/s,Wf=-1.094 m/s,Vf=2.981 m/s,满足着陆速度约束,且竖直速度分量较小,经过姿态调整段,可以实现竖直安全着陆。
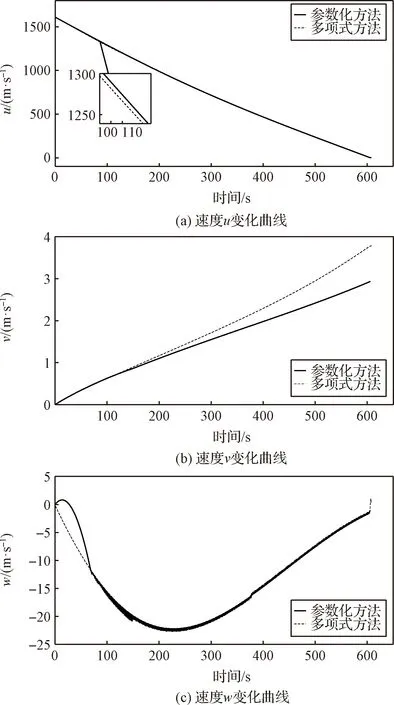
图3 速度变化曲线Fig.3 The velocity curve of soft landing
如图4和图5所示,月球软着陆的最终着陆高度为1741.03 km,水平行程约为638.7 km。
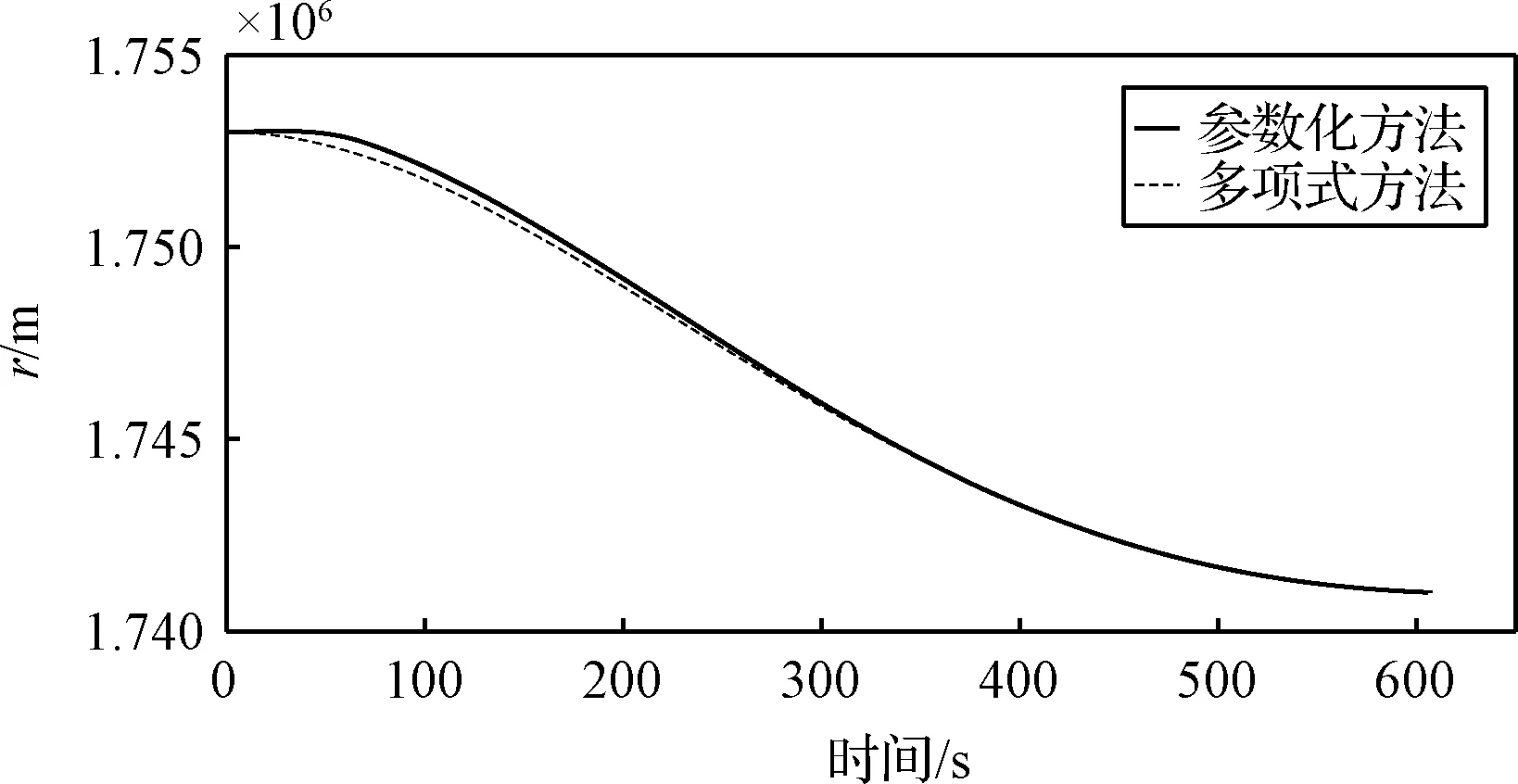
图4 高度变化曲线Fig.4 The height curve
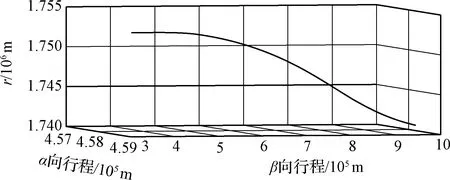
图5 着陆轨迹曲线Fig.5 The trajectory of soft landing
图6所示为月球探测器的推力仰角的变化曲线,可以看出采用改进的多项式制导律在动力下降段末端需要进行固定参数,否则会产生跳变,而CVP方法得到的控制曲线更加平缓,在450 s后基本不再需要再规划,更具有实现性。
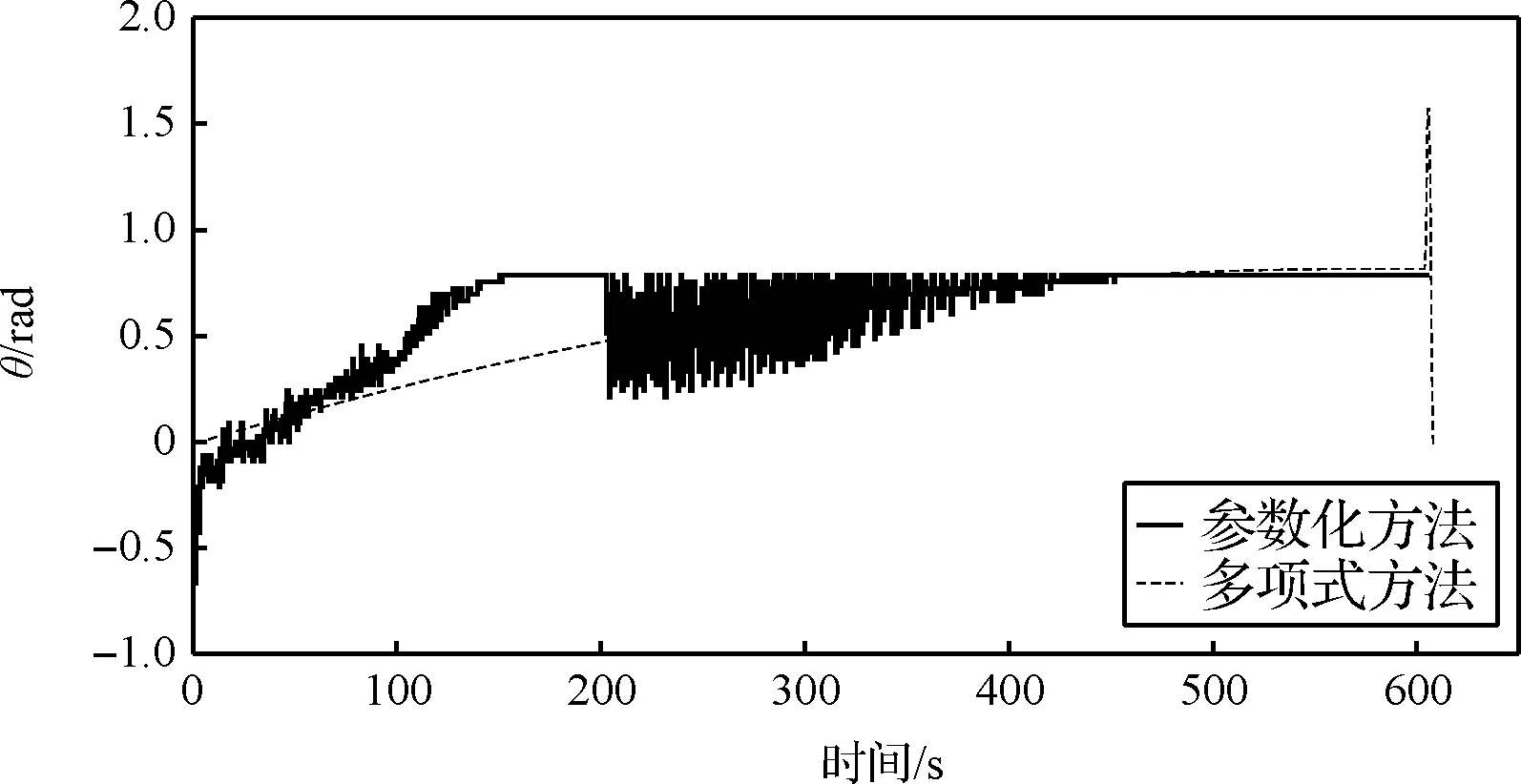
图6 控制变量θ变化曲线Fig.6 The control variable θ curve
5 着陆精度仿真分析
下面给出测量误差情况下采用变推力方案的着陆参数和着陆误差分布情况。以下关于误差的分析均采用蒙特卡罗打靶,打靶次数为700次,假设各误差均符合正态分布。
图7给出了月球探测器在月心惯性坐标系3个方向上初始着陆点在1753±1 km的散布示意图。本文中给出的动力下降段起始点误差散布分别在500 m、1 km和3 km范围的球体内。

图7 着陆起始点分布示意图Fig.7 Initial landing site dispersion
图8给出了700次打靶计算中动力下降段结束时高度误差的散布情况。图8(a)所示是起始点误差在±500 m情况下动力下降段结束时高度误差和着陆速度的散布情况,可以看出在绝大多数情况下,高度误差不大于30 m,符合着陆安全要求,且90%以上的竖直速度小于1 m/s,水平速度不大于1.5 m/s;图8(b)所示为起始点误差±1000 m时的误差分布情况,可以看出轨迹的高度误差依然保持在50 m以内,大致满足σ分布准则,且竖直方向的速度在±1 m/s以内,水平方向的速度绝大多数在1~2 m/s之间,符合仿真给了的精度要求;图8(c)所示为高度误差±3000 m时的误差分布情况,多数误差分布在±100 m以内,满足σ分布准则,半数以上分布在±20 m内,竖直方向的着陆速度不大于1 m/s,水平方向的着陆速度不大于4 m/s,为姿态调整段安全着陆提供保障。
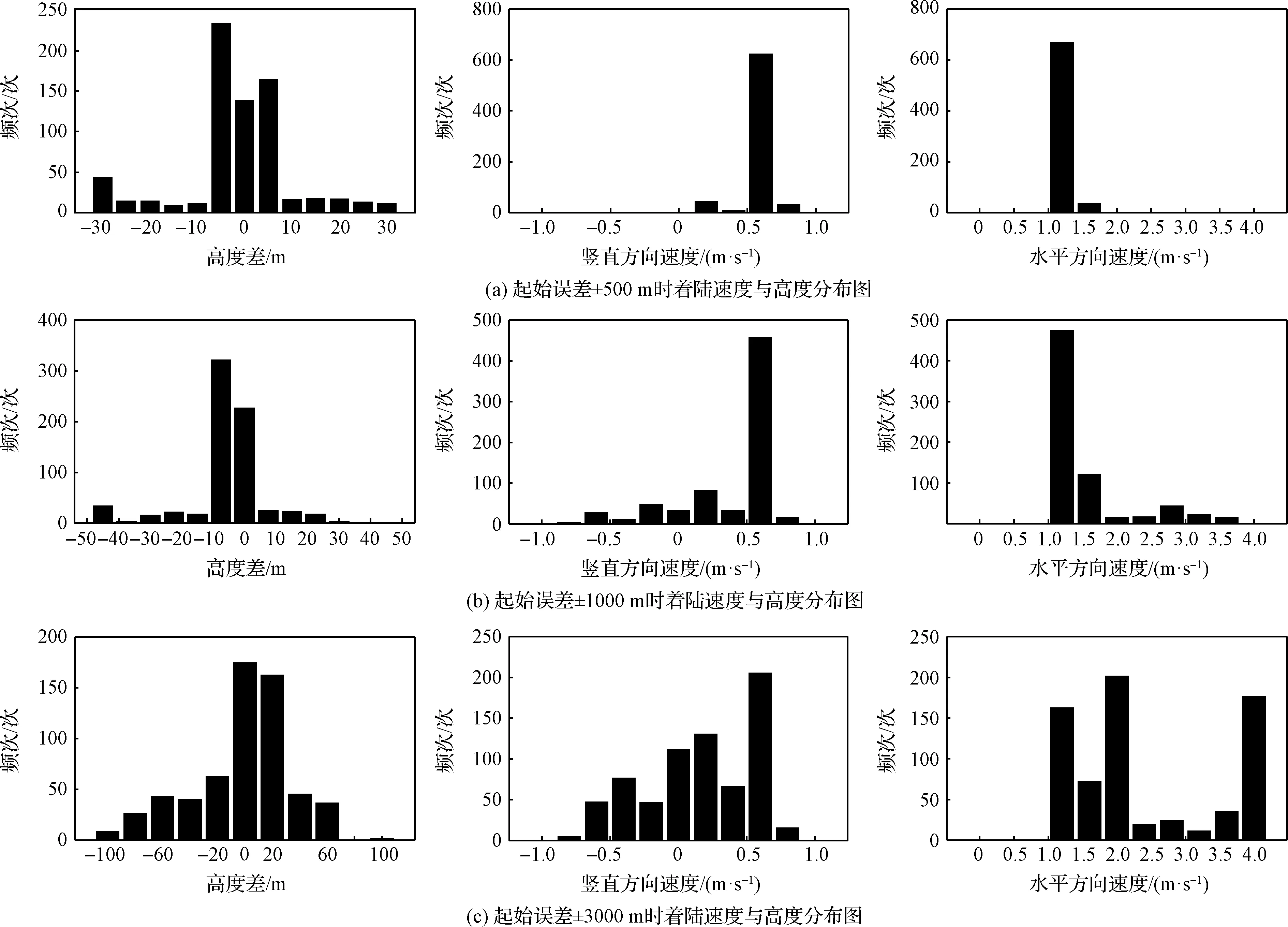
图8 高度误差分布情况Fig.8 Dispersion in final altitude
图9给出了700次打靶计算中着陆轨迹的散布情况。图9(a)、(b)和(c)分别给出了起始点误差±500 m、±1000 m和±3000 m情况下动力下降段结束时轨迹的散布情况,可以看到动力下降段结束时,着陆轨迹大致分布在同一平面上,证明算法满足任务要求的着陆高度精度要求。
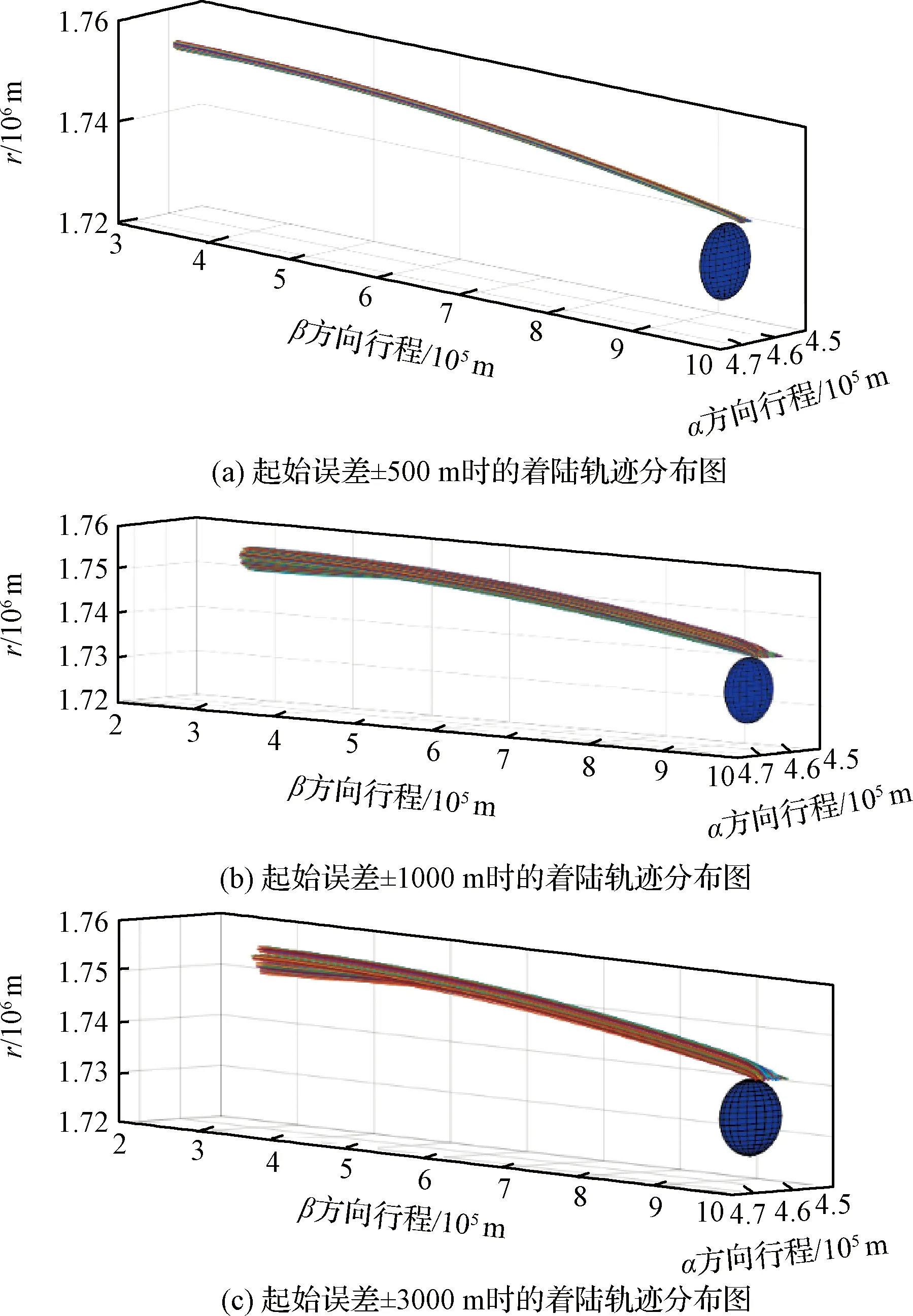
图9 轨迹分布图Fig.9 3D landing trajectories MC simulation
6 结 论
本文提出了一种改进的显式制导方法,简化控制变量,避免了制导末段剩余时间发散问题,并利用控制变量参数化方法将着陆轨迹分段,引入时间尺度变换方法,运用经典的非线性规划方法求解每段控制变量最优数值解,最终得到月球探测器动力下降段燃料最优着陆轨迹。仿真结果表明,相比于传统的显式制导律,本文提出的方法燃料消耗更少。蒙特卡罗打靶实验证明,本文提出的算法在初始着陆点存在±20%误差的情况下,依然能够保证足够的着陆高度和速度裕量,保障姿态调整段和垂直着陆段探测器安全着陆。

