地月高能共振循环轨道的快速计算及最优选择
郑 越,泮斌峰,唐 硕
(1.西安航空学院,西安 710077;2. 西北工业大学航天学院,西安 710072)
0 引 言
地月循环轨道是周期性往返于地球与月球之间并在地球和月球附近不做停留的一类周期轨道。运行在循环轨道上的探测器不需要轨道机动或只需进行少量轨道机动即可运载人员和物资往返于地月之间。与直接转移相比,循环飞行器能够被重复使用,转移过程中不需要消耗大量能量重新将星际转移飞行器从地面运送到星际转移入轨点。因此,循环轨道可以用于完成长期的、持续的月球探测任务,是一种有研究价值和发展潜力的轨道转移方案。
地月循环轨道最早在1957年由Egorov[1]发现。随后,研究人员找到了更多的轨道[2-4],其中最有实践价值的是1963年Arenstorf[5-6]发现的两条轨道,这两条轨道被命名为Arenstorf轨道,后来被用于阿波罗计划。Anthony等[7]对不同循环轨道的特征进行了归纳。在国内,杨雷等[8]提出了地月循环轨道重访轨道空间站系统的概念,初步研究了基于空间站的载人月球探测飞行任务方案。张文博等[9]研究了地月循环轨道的动力学建模方法。罗宗富等[10]对一类特殊的地月循环轨道——双月旁转向轨道进行了研究。文献[11-12]设计了周期轨道的一般计算方法,所计算出的轨道包括地月循环轨道。文献[13]对地月系统下的轨道进行分类,并分析了地月循环轨道的低能转移特性。文献[14]通过不变流形实现不同共振比循环轨道的同宿连接。
在限制性三体问题中,当质量比参数μ→0时,周期轨道经变形后收敛于二体的非退化周期轨道,其中包括开普勒椭圆弧与碰撞奇点,碰撞奇点可以由质量较小的主天体的近似开普勒轨道替代。Poincaré[15]将变形后不包含碰撞奇点的开普勒轨道构成的周期轨道命名为第一类周期轨道,变形后包含碰撞奇点的开普勒轨道构成的周期轨道命名为第二类周期轨道。在地月三体系统中,与第一类周期轨道相比,第二类周期轨道的近月点距离月球较近,具有更高的工程应用价值。但是,月球相当于一个碰撞点,靠近碰撞点的开普勒椭圆轨道也会发生相应的形变。1968年,Hénon[16]根据受碰撞点影响的第二类周期轨道的组成弧段对第二类周期轨道族进行分类。2013年,Casoliva等[17]将地月循环轨道分为与月球公转轨道具有一定共振关系的高能共振循环轨道和利用平动点而实现的低能循环轨道。满足第二类周期轨道特性的高能共振循环轨道与月球距离较近,易于实现与月球停泊轨道的交会,且这类轨道与月球公转具有共振特性,所以成为当前研究的重点。
针对满足第二类周期轨道特性的地月高能共振循环轨道,目前的轨道计算方法主要有延拓法[18]和圆锥曲线拼接法[19]。延拓法根据二体系统下的开普勒椭圆轨道状态量,通过质量比参数μ的逐渐增大而得到三体系统下的地月循环轨道。Casoliva等[20]根据探测器与月球的共振关系,通过延拓法计算出三体系统下的地月循环轨道。这种方法在逐渐增大μ的过程中,必须计算出一系列循环轨道后才能最终得到地月系统下的循环轨道,计算量较大。而且该方法在构造共振比大于2.3,即具有更小的近地点半径和近月点半径的地月循环轨道时会失败。圆锥曲线拼接法根据开普勒椭圆轨道构建第二类周期轨道的初值。张文博[21]采用圆锥曲线拼接法,根据轨道弧段的分类设计了共振比为1∶1的五类地月系统循环轨道,并给出了最优轨道。该方法由于缺乏对轨道拓扑特性的分析,构造出的某些类型的地月循环轨道的共振特性发生了改变,而且尚未构造出共振比大于2.3的循环轨道。
针对现有的地月高能共振轨道计算方法所存在的计算量大、有可能改变共振特性和不能构造共振比大于2.3的轨道等缺点,本文提出一种高能共振循环轨道的快速计算方法。该方法根据开普勒椭圆轨道在受碰撞点影响后的组成弧段对满足第二类周期轨道特性的地月高能共振循环进行分类;利用μ→0时二体开普勒椭圆轨道的共振比和拓扑结构,计算出三体系统下的地月高能共振循环轨道;最后,根据能量、稳定性、时间周期、距地球和月球的距离,选择出适用于长期月球探测任务的最优轨道。
1 动力学模型
考虑地月圆型限制性三体问题(Circular restricted three-body problem,CRTBP),质量可以忽略的探测器在地球和月球两个主天体的引力作用下的运动,其中主天体绕其公共质心做匀速圆周运动[22-24]。归一化地球质量m1和月球质量m2之比为单位质量(m1/m2=0.0123),则:
(1)

(2)
其中:Ω为旋转坐标系下的等效势能:
(3)
设矢量r1,r2为探测器到两个主天体的距离,有:
(4)
CRTBP系统中,存在雅可比积分如下:
(5)
在地月三体系统中,单位长度为地月之间的距离L=3.844×105km,单位时间为T=104 h,单位速度为V=1024 m/s。
2 轨道分类
在地月三体系统下,与质量比参数μ→0时的二体开普勒椭圆轨道相比,月球相当于一个碰撞点,开普勒椭圆轨道经过碰撞点附近时,轨道的部分弧段会在月球引力影响下而发生形变。根据轨道发生形变后的组成弧段,能够对高能共振循环轨道的类型进行划分。


图1 轨道弧段Fig.1 Orbit arcs
根据受月球影响后飞行器轨道的组成弧段和运动方向,可将由S弧构成的高能共振循环轨道分为六类,其分类方法见表1。由于S弧对称于开普勒椭圆轨道的拱线,则由S弧构成的循环轨道在旋转坐标系下也具有对称性。

表1 第二类周期轨道分类Table 1 Classification of second species period orbits
3 二体开普勒椭圆轨道
对于地月CRTBP,如果忽略月球质量,即质量比参数μ→0,系统近似为以地球为中心的二体系统。那么μ→0时的地月循环轨道在地心惯性坐标系下由开普勒椭圆轨道构成。根据轨道共振比,能够得出μ→0情况下的地月循环轨道。
3.1 轨道共振比
在地月CRTBP下,假设质量比参数μ→0,则探测器做开普勒椭圆运动,并且其运动周期为:
(6)
其中:a为椭圆轨道半长轴,μE等价于地球质量,而在归一化单位情况下,有μE=1。由于月球公转周期TM=2π,所以探测器开普勒椭圆运动与月球公转之间的共振比[25-26]为:
(7)
式中:p与q互质,表示轨道共振比,M与K分别表示探测器和月球运行的圈数,即探测器绕地球运转M圈的同时,月球绕地球运转K圈。开普勒椭圆轨道是在地心惯性坐标系下建立的。根据轨道共振特性,如果令椭圆轨道围绕地球运转M圈,则月球围绕地球运转K圈。那么,此时开普勒椭圆轨道在地月质心旋转坐标系下也形成首尾相连的周期轨道,且轨道周期为:
T=2Kπ
(8)
根据式(6)和式(7),可知开普勒轨道半长轴与轨道共振比之间的关系为:
(9)
因此,通过探测器和月球围绕地球运行的圈数,可以得到循环轨道与月球公转的共振比,进而计算出椭圆轨道半长轴,其结果见表2(共振比为互质数,如p∶q=M∶K=4∶2=2∶1)。

表2 探测器轨道半长轴(归一化单位)与共振比的关系Table 2 Relation between the semimajor axis (normalized units) and resonances ratio of the spacecraft orbit
3.2 轨道特征参数
构造μ→0情况下的地月循环轨道需要筛选出适合的轨道共振比,所以需要考虑如下参数:
1)月球公转圈数约束
月球公转周期为27天。对于由开普勒椭圆轨道组成的循环轨道,轨道周期由月球公转圈数来决定。在空间转移任务中,尤其是循环轨道用于载人任务时,通常希望轨道周期尽可能短。
2)半长轴约束
一方面,考虑探测器轨道最小近地点距离rPEmin=0.017(距地球表面167 km),最小近月点距离rPMmin=0.0048(距离月球表面100 km),则开普勒椭圆轨道的长轴半径必须满足如下关系:
2a>1+rPEmin+rPMmin
(10)
另一方面,开普勒椭圆轨道的半长轴不宜过大,因为过大的半长轴意味着较远的近地点或者近月点距离,也会带来较高的转移能耗和较长的周期。
3.3 开普勒循环轨道
综合构造循环轨道时需要的轨道特征参数条件,参照表2,选择共振比为2∶1和5∶2的开普勒椭圆轨道。
对地月三体系统下循环轨道进行建模,需要先根据CRTBP动力学方程和轨道共振比构造出在μ→0情况下的循环轨道,再根据轨道状态量将其扩展到μ=0.01215的CRTBP动力学方程。设μ→0时开普勒椭圆轨道近地点距离为rPE,远地点距离为rAE,则有:
rPE+rAE=2a
(11)
图2为μ→0时地月系统的开普勒椭圆轨道,近地点和远地点分别为P和Q,由于地月之间的距离rEM=1,则远地点到月球轨道的距离rQM能够通过下式计算:
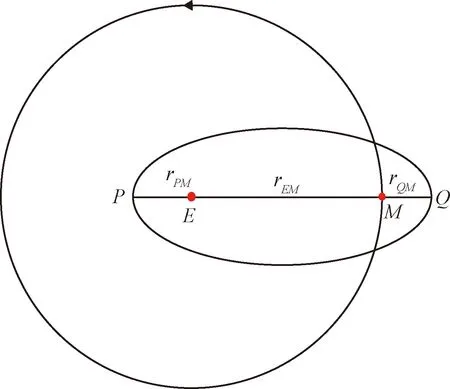
图2 地月系统μ→0时的开普勒轨道Fig.2 Keplerian orbits in the Earth-Moon system when μ→0
rQM=rAE-rEM=2a-rPE-1
(12)
对于共振比为2∶1和5∶2的椭圆轨道,近月点rPM=rQM,根据最小近地点距离和最小近月点距离,可以得到rPE和rPM的取值范围为:
(13)
而轨道的近地点和近月点满足如下关系:
rPE+rPM=2a-1
(14)
在μ→0的情况下构造循环轨道需要给出轨道初始状态和轨道周期。循环轨道的周期为2qπ,轨道初始状态的设置分为顺行和逆行两种情况,轨道在质心旋转坐标系下的初始状态分别为:
(15)
只要近地点和近月点距离选择合适,便可通过微分修正迭代得到循环轨道。令rPE=rPM=(2a-1)/2,相应的可以得到rAE=2a-rPE。图3、图4、图5和图6分别为地月系统下μ→0时的开普勒椭圆轨道在质心旋转坐标系(‘o’代表轨道起点)和地心惯性坐标系(‘o’和‘+’分别代表轨道起点和终点)下的运动轨迹。其中,图3和图4分别为共振比为2∶1的开普勒顺行和逆行轨道;图5和图6分别为共振比为5∶2的开普勒顺行和逆行轨道。

图3 共振比为2∶1的顺行开普勒轨道Fig.3 Prograde Keplerian orbits with resonance ratio 2∶1

图4 共振比为2∶1的逆行开普勒轨道Fig.4 Retrograde Keplerian orbits with resonance ratio 2∶1
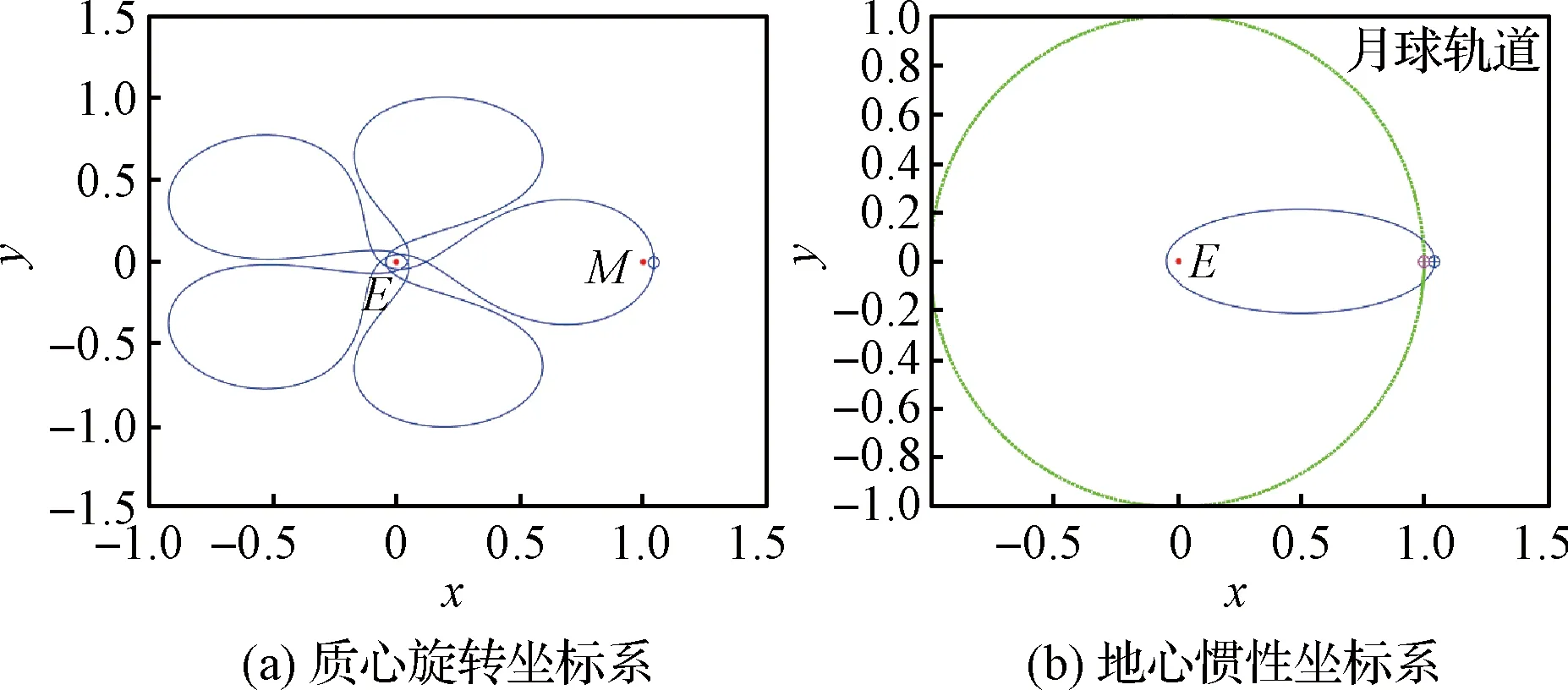
图5 共振比为5∶2的顺行开普勒轨道Fig.5 Prograde Keplerian orbits with resonance ratio 5∶2

图6 共振比为5∶2的逆行开普勒轨道Fig.6 Retrograde Keplerian orbits with resonance ratio 5∶2
4 高能共振轨道的计算
在地月CRTBP中,当忽略月球引力时,三体系统下的循环轨道可以演变为二体系统下围绕地球运行数圈的开普勒椭圆轨道,且循环轨道与月球公转周期存在严格的共振比;如果对二体系统下开普勒椭圆轨道引入月球扰动,椭圆轨道运行至月球附近时会发生形变,二体系统下由开普勒轨道组成的循环轨道也会根据月球引力的影响而演变成不同的轨道类型。本节将μ→0情况下的二体开普勒轨道演变到μ=0.01215下的地月CRTBP中,并根据轨道类型计算出相应的地月循环轨道。
4.1 拓扑结构分析
当循环轨道存在共振特性时,其共振比可根据轨道周期和轨道以地球为中心的卷绕数[27-28]来计算。循环轨道的卷绕数W(γ,H)是一个整数,表示循环轨道γ绕定点H运动的总圈数。如果轨道沿逆时针方向运动,则卷绕数为正数;如果轨道沿顺时针方向运动,则卷绕数为负数。设循环轨道的周期为T,则探测器和月球绕地球旋转的圈数M和K分别为:

(16)
同一弧段类型的循环轨道如果在旋转坐标系下有相同的卷绕数,则在惯性坐标系下就有相同的共振比。当质量比参数从μ→0演变到μ=0.01215时,相对于地球,循环轨道也必然保持相同的拓扑结构。所以,可将循环轨道在旋转坐标系下的卷绕数作为计算三体系统下循环轨道的条件。
与表2中不同类型的地月循环轨道相对应,可将循环轨道卷绕数作为计算循环轨道的判断条件。本文研究共振比为2∶1和 5∶2的地月循环轨道。根据式(16)可判断:AⅠ类和BⅠ类循环轨道逆时针绕地心运行一圈;AⅡ类和BⅡ类循环轨道顺时针绕地心运行三圈。C类轨道在一个周期内通过月球正面和背面,因此可认为是由轨道运行方向相同的A类和B类循环轨道组成,周期为4π的C类循环轨道的共振比为2∶1。其中,CⅠ类轨道逆时针绕地心运行两圈;CⅡ类轨道顺时针绕地心运行六圈。
4.2 时间条件
在地月CRTBP下,假设μ→0,则探测器运行轨道为开普勒椭圆轨道。μ从μ→0增大到μ=0.01215,系统引入月球扰动。当探测器运行至月球附近时,开普勒轨道受月球引力的影响会发生形变而演化出CRTBP下的循环轨道。根据轨道的形变,可估计μ=0.01215时地月循环轨道的周期。
AⅠ类和AⅡ类循环轨道的近月点出现在月球背面;BⅠ类和BⅡ类循环轨道的近月点出现在月球正面;CⅠ类和CⅡ类循环轨道在一个周期内分别经过月球正面和反面。由此可知:AⅠ类和AⅡ类循环轨道由椭圆轨道及其一段内弧组成;BⅠ类和BⅡ类循环轨道由椭圆轨道及其一段外弧组成;CⅠ类和CⅡ类循环轨道由椭圆轨道及其内弧和外弧共同组成。所以,C类轨道的时间周期近似于月球公转周期的整数倍,A类、B类轨道的时间周期需要通过计算来预估。
图7为地月三体系统下A类和B类循环轨道运行轨迹示意图。椭圆轨道的长轴连接近地点P和远地点Q并与月球公转圆轨道交于点N。以新演化出的循环轨道的近月点S0为起点,则S0与月球公转的起点M0和地心E位于同一条直线上,那么轨道的近月点距离为rS0M0。设循环轨道的终点为S1,则将S1与地心连接,连线与月球轨道相交于M1,因此不同类型的循环轨道的时间周期可以近似为:

图7 地月CRTBP中不同类型的循环轨道示意图Fig.7 Different types of cycler in the CRTBP
AⅠ类:T=TS0PS1+2π(p-1)a3/2=2qπ-TM1NM0
AⅡ类:T=TS0PS1+2π(p-1)a3/2=2qπ+TM0 NM1
BⅠ类:T=TS0QS1+2π(p-1)a3/2=2qπ+TM0 NM1
BⅡ类:T=TS0QS1+2π(p-1)a3/2=2qπ-TM1 NM0
CⅠ、CⅡ类:T=2π(p-1)a3/2=2qπ
其中:
TM0 NM1=TM1NM0=4θπ
(17)
令椭圆轨道中除了地心外的另一个焦点为F,则地心E与F之间的距离为:
rEF=2(a-rPE)
(18)
设置近月点距离为rM0S0,地心与近月点S0之间的距离为:
(19)
那么S0与F之间的距离rS0F可以通过下式计算:
rS0F=2a-rES0
(20)
由此可以通过余弦公式计算出θ的值,进而预估地月循环轨道的周期。
4.3 计算方法
对于地月CRTBP,μ=0.01215时的地月循环轨道是μ→0情况下的共振轨道通过月球附近时因月球引力导致轨道变形而得到的。尽管二体开普勒椭圆轨道演变为三体系统下的循环轨道时,通常会因为受到月球引力的影响而改变轨道的近月点高度,但是它们具有相同的拓扑结构。所以,三体系统下的循环轨道状态量可通过二体开普勒椭圆轨道来预估。
循环轨道的计算方法通过以下三步实现:
1) 选定循环轨道类型和近月点距离rS0M0, 根据时间条件估计循环轨道的周期,轨道初始点速度的大小通过二体开普勒椭圆轨道组成的参考周期轨道的雅可比常数C来估算的,速度方向垂直向下。
2) 以μ→0情况下的二体开普勒椭圆轨道的拓扑结构作为参考周期轨道,根据估算时间和卷绕数,利用微分修正法计算出地月循环轨道。
3) 如果通过微分修正法不能计算得到循环轨道,则回到步骤(1),调整二体开普勒椭圆轨道的近月点距离,直到计算出地月循环轨道为止。
图8、图9、图10、图11、图12和图13分别为通过2∶1共振轨道演化得到的不同类型的循环轨道;图14、图15、图16和图17分别为通过5∶2共振轨道演化得到的不同类型的循环轨道。循环轨道的近月点距离月球表面均为10000 km。

图8 共振比为2∶1的AⅠ类地月循环轨道Fig.8 Type AⅠ Earth-Moon cyclers with 2∶1 resonance

图9 共振比为2∶1的AⅡ类地月循环轨道Fig.9 Type AⅡ Earth-Moon cyclers with 2∶1 resonance

图10 共振比为2∶1的BⅠ类地月循环轨道Fig.10 Type BⅠ Earth-Moon cyclers with 2∶1 resonance

图11 共振比为2∶1的BⅡ类地月循环轨道Fig.11 Type BⅡ Earth-Moon cyclers with 2∶1 resonance

图12 共振比为2∶1的CⅠ类地月循环轨道Fig.12 Type CI Earth-Moon cyclers with 2∶1 resonance
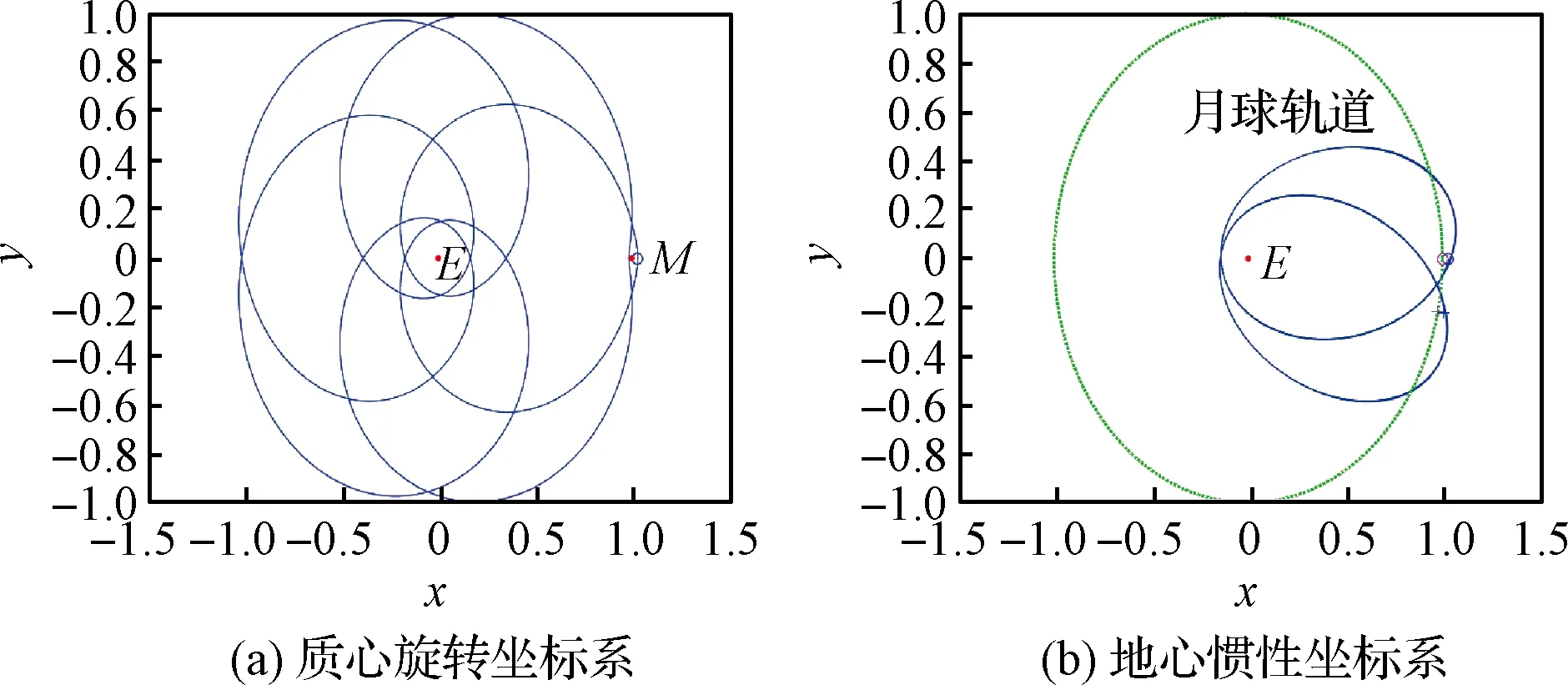
图13 共振比为2∶1的CⅡ类地月循环轨道Fig.13 Type CⅡ Earth-Moon cyclers with 2∶1 resonance

图14 共振比为5∶2的AⅠ类地月循环轨道Fig.14 Type AⅠ Earth-Moon cyclers with 5∶2 resonance
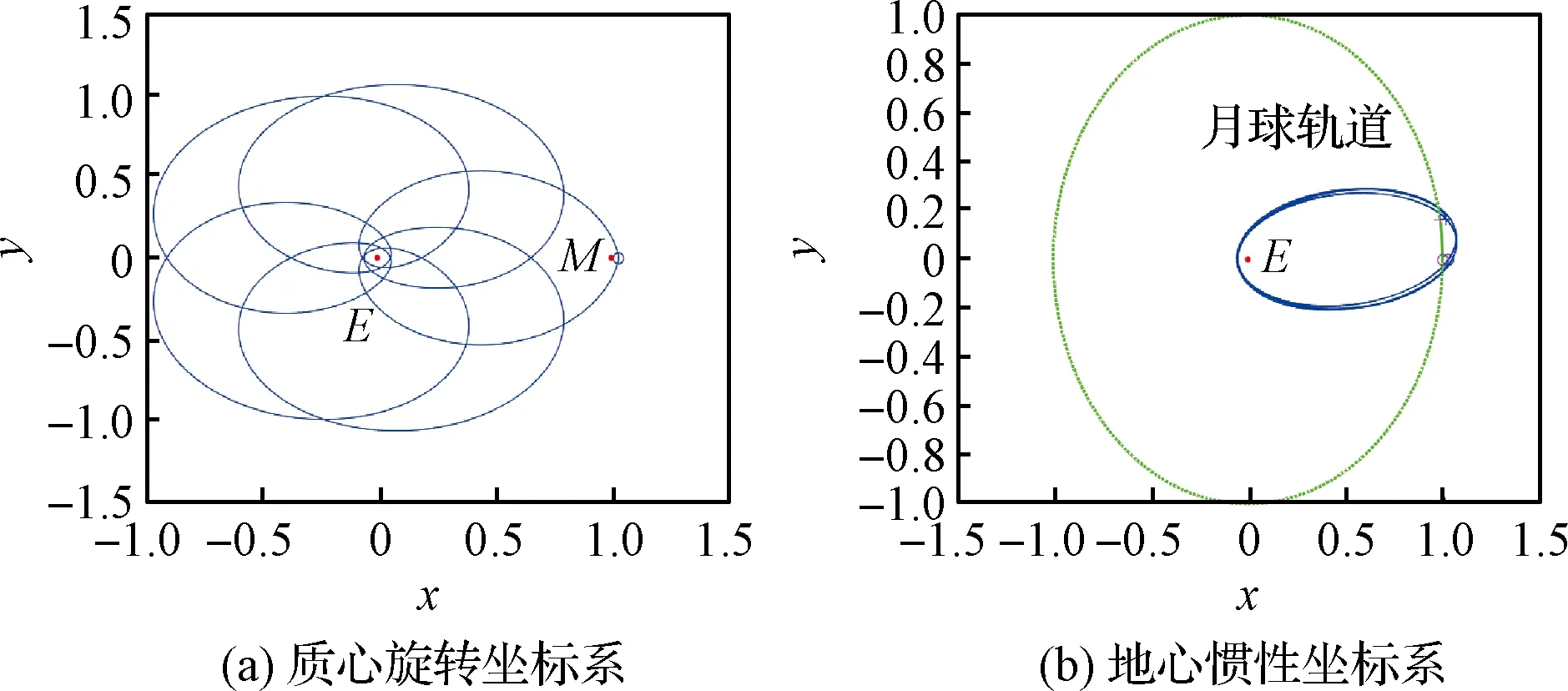
图15 共振比为5∶2的AⅡ类地月循环轨道Fig.15 Type AⅡ Earth-Moon cyclers with 5∶2 resonance

图16 共振比为5∶2的BⅠ类地月循环轨道Fig.16 BⅠ Earth-Moon cyclers with 5∶2 resonance
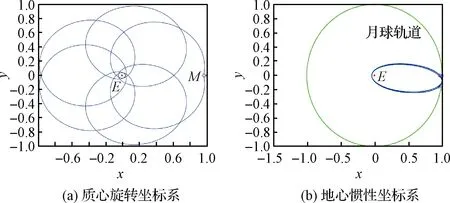
图17 共振比为5∶2的BⅡ类地月循环轨道Fig.17 Type BⅡ Earth-Moon cyclers with 5∶2 resonance
将本文方法与现有方法相比较。文献[20]将二体系统下的椭圆轨道初始状态作为计算初值,利用延拓法,通过不断增加μ计算出不同共振比的地月循环轨道。该方法计算量大,且在构造共振比大于2.3的轨道时未取得成功。文献[21]计算了共振比为2∶1的地月高能共振循环轨道,但是所得到的轨道中,BⅠ类和BⅡ类轨道的共振比发生了改变。本文方法能够准确、快速、有效的计算出地月高能共振循环轨道,其中包括共振比为5∶2的轨道(共振比大于2.3)。
4.4 轨道延拓
轨道延拓是通过延拓法得到与已知轨道相关的一族轨道。方法是选择轨道初始状态参数作为延拓参数,改变延拓参数,并利用微分修正法对其进行计算,从而得到与已知参考轨道相关的轨道族[29]。
最常用的延拓法为参数延拓法,通常选取有明确物理意义的延拓参数,例如位置参数、雅可比常数。为了保证轨道能够延拓成功,参数的改变不能过大。图18和图19分别为通过共振比为2∶1和5∶2的不同类型的地月循环轨道改初始位置后延拓得到的一系列循环轨道。
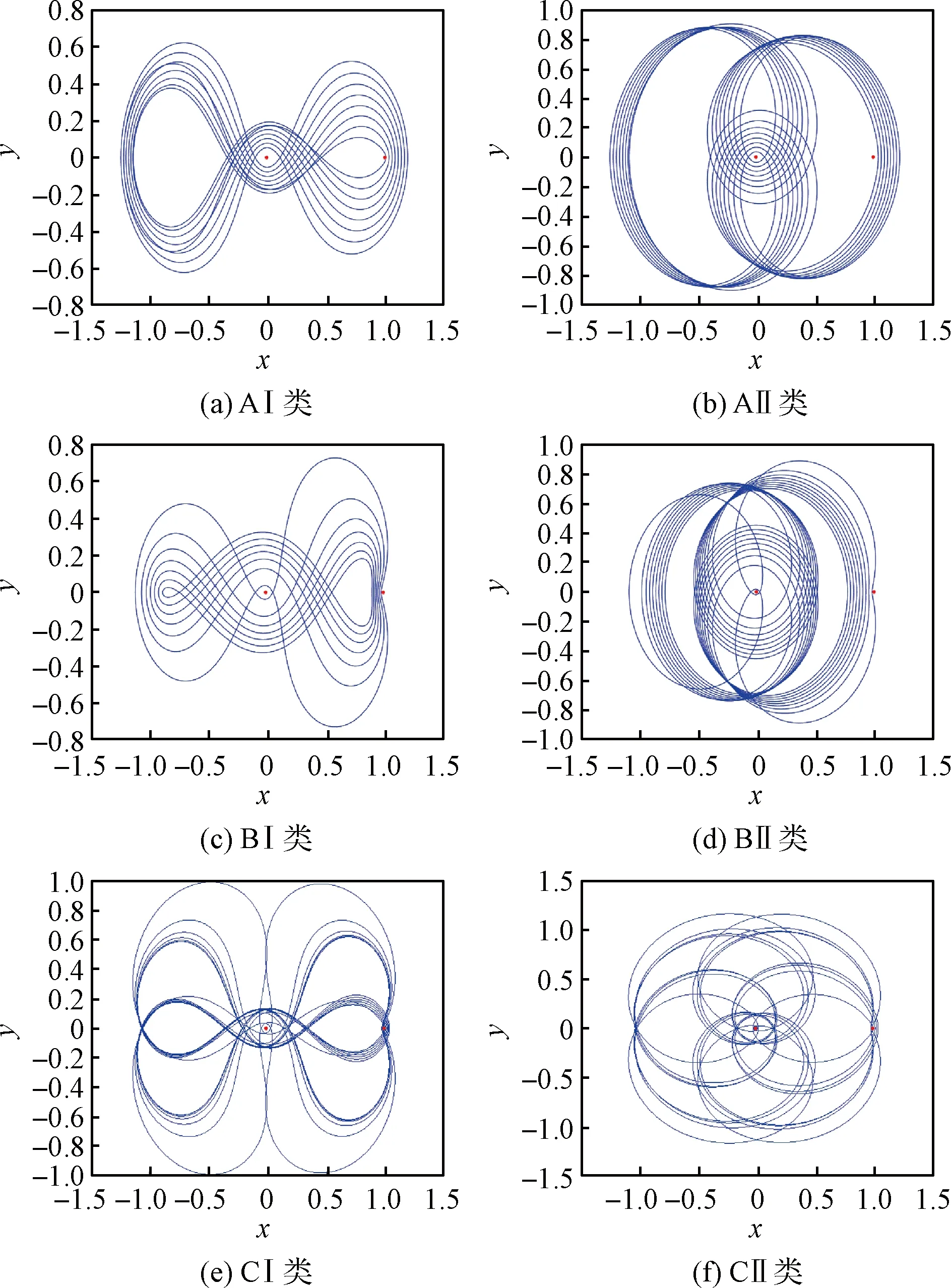
图18 不同类型地月循环轨道的延拓(共振比2∶1)Fig.18 Continuation of different types of Earth-Moon cyclers (2∶1 resonance)
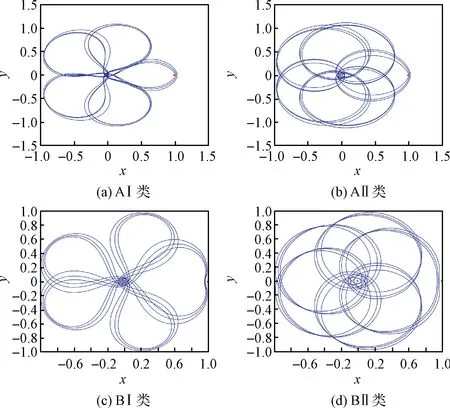
图19 不同类型地月循环轨道的延拓(共振比5∶2)Fig.19 Continuation of different types of Earth-Moon cyclers (5∶2 resonance)
5 最优轨道选择
在地月CRTBP中,存在无数个地月循环轨道,需要综合轨道的各项性能指标,找出适用于长期地月任务的循环轨道。
衡量地月循环轨道优劣的指标主要有能量、稳定性、时间周期、距离地球和月球的距离等。其中,轨道的能量直接决定了其用于地月转移时能耗的大小。显然,逆行轨道比顺行轨道具有更高的能量,轨道转移时也相应的需要更高的能耗。因此,用于地月任务的循环轨道只考虑顺行轨道。图20、图21、图22、图23和图24分别为共振比为2∶1的AⅠ类循环轨道、共振比为2∶1的BⅠ类循环轨道、共振比为5∶2的AⅠ类循环轨道、共振比为5∶2的BⅠ类循环轨道和共振比为2∶1的CⅠ类循环轨道的近地点距离地表高度、周期、雅可比常数和稳定判据随近月点距离月球表面高度变化时的性能指标。根据稳定性判据,不能到达月球背面的BⅠ类轨道不稳定,容易受到小扰动的影响,不适用于长期地月任务,所以只有AⅠ类和CⅠ类轨道可选择。再进一步对比循环轨道的各项指标,当CⅠ类轨道稳定时,近地点距离地球表面高度dM>25000 km,该类轨道不适用于实现地月转移任务。因此,可供选择的只有AⅠ类循环轨道。

图20 共振比2∶1的AⅠ类循环轨道的不同状态量随近月点高度的变化Fig.20 Variation of different state of type AⅠ cyclers with 2∶1 resonance as the increasing perilune distance

图21 共振比2∶1的BⅠ类循环轨道的不同状态量随距离月球表面高度的变化Fig.21 Variation of different states of type BⅠ cyclers with 2∶1 resonance as the increasing perilune distance

图22 共振比5∶2的AⅠ类循环轨道的不同状态量随距离月球表面高度的变化Fig.22 Variation of different states of type AⅠ cyclers with 5∶2 resonance as the increasing perilune distance

图23 共振比5∶2的BⅠ类循环轨道的不同状态量随距离月球表面高度的变化Fig.23 Variation of different states of type BⅠ cyclers with 5∶2 resonance as the increasing perilune distance

图24 共振比2∶1的CⅠ类循环轨道的不同状态量随距离月球表面高度的变化Fig.24 Variation of different states of type CⅠ cyclers with 2∶1 resonance as the increasing perilune distance
根据图22(d)可知,满足稳定性判据|s|<2的地月循环轨道距月球表面距离dM的可选区间为[11500 km,15400 km]。由图22可知,在该区间内,地月循环轨道距月球表面距离越远,轨道距离地球表面越近,轨道周期越长,雅可比积分越小。在地月循环轨道的近地点和近月点,通过施加脉冲能够分别实现与地球停泊轨道和月球停泊轨道之间的转移[30]。图25为dM∈[11500 km,15400 km]情况下探测器从地球停泊轨道进入地月循环轨道和从地月循环轨道进入月球停泊轨道时所需要的脉冲。与探测器从地球停泊轨道进入循环轨道所需要的脉冲量相比,探测器从不同高度的循环轨道进入月球停泊轨道所需要的脉冲量非常接近。所以,在保证稳定性的前提下,循环轨道近月点距月球越近,其近地点距地球越远,转移过程中所需要的总能耗越低;循环轨道近月点距月球越远,其近地点距地球越近,转移过程中所需要的总能耗越高。当dM=11500 km时,近地点距离地表高度dE=2588 km,探测器从地球停泊轨道进入循环轨道所需要的能耗为ΔvE=2636 m/s,探测器从循环轨道进入月球停泊轨道所需要的能耗为ΔvM=574 m/s,整个转移过程所需要的能耗最低,为3210 m/s;当dM=15400 km时,dE=1358 km,近地点距离地球最近,探测器从地球停泊轨道进入循环轨道所需要的能耗为ΔvE=2848 m/s,探测器从循环轨道进入月球停泊轨道所需要的能耗为ΔvM=576 m/s,整个转移过程所需要的能耗为3424 m/s。

图25 共振比5∶2的AⅠ类循环轨道随近月点高度变化时所需要的脉冲量Fig.25 The required pulses for type AⅠ cyclers with 5∶2 resonance as the increasing perilune distance
文献[21]从共振比为2∶1的AⅠ类轨道中选择出合适的轨道用于循环方案,其优点是稳定性高、周期短,但是其近地点半径和近月点半径过大,分别为72326 km和67674 km。本文所构造的共振比为5∶2的AⅠ类轨道尽管周期稍长,但其具有较小的近地点半径和近月点半径,更适合在地球和月球间进行轨道转移。另外,由于文献[21]中所选择的地月循环轨道距离地球过远,需要额外增加一段轨道来实现循环轨道的入轨设计。当探测器从距离地表500 km的地球停泊轨道出发时,探测器从地球停泊轨道进入循环轨道所需要的能耗为3411 km/s,转移时间约为6天,且未考虑探测器从循环轨道进入月球停泊轨道所需要的能耗。与之相比,本文选择的循环轨道的近地点半径和近月点半径较小,可以通过一个脉冲量直接实现循环轨道与地球停泊轨道和月球停泊轨道之间的转移,不需要入轨的过渡时间,且转移过程中所需要的能耗较低。
6 结 论
本文以二体开普勒椭圆轨道为参考,根据轨道共振比与半长轴的关系对地月高能共振循环轨道进行了构造,快速计算出圆型限制性三体问题下地月高能共振循环轨道的初始状态。克服了现有方法存在计算量大、有可能改变共振特性和不能构造共振比大于2.3的地月循环轨道等缺点。将能量、稳定性、时间周期、近地点高度和近月点高度作为衡量地月循环轨道优劣的指标,对高能共振循环轨道进行了最优选择。本文研究的高能共振循环轨道对长期月球探测任务的实现具有重要的意义,下一步需要将现有成果推广到三维空间内,并进一步对结构较为复杂的地月循环轨道进行研究。

