基于MADDPG的多无人机协同任务决策
李 波,越凯强,甘志刚,高佩忻
(西北工业大学电子信息学院,西安 710114)
0 引 言
近年来,无人机不但在房地产[1]、农业[2]、安保[3]、搜索救援[4]、地面勘探[5]、特殊物流[6]等许多商业领域取得了不俗的成绩[7],而且在军事领域也大放异彩,出色的完成了许多有人驾驶飞机难以完成的任务。然而,单个无人机受其飞行距离、飞行范围、弹载能力和应对突发状况能力的制约,难以发挥出其应有的作战效能。因此现有的研究都是基于多无人机系统[8]开展的,相比于单个无人机,多无人机系统具有更强的作战优势。对于多无人机系统而言,任务决策问题是重中之重,各国军事专家都在为如何解决无人机的任务决策问题而不断努力。
各国学者对于多无人机任务决策的研究都在如火如荼的进行,在多无人机协同搜索[9]、跟踪[10]、任务分配[11-12]、航迹规划[13]和编队控制[14]等研究中,都已取得了不俗的成果。同时,深度学习和强化学习的快速发展,也极大地加快了无人机系统智能化[15]的发展进程。赖俊和饶瑞[16]提出了一种基于空间位置标注的好奇心驱动的深度强化学习方法,解决了室内无人机随机目标搜索效率不高、准确率低等问题。Xu等[17]设计了一种新型仿生变形无人机模型,并采用了深度确定性策略梯度(Deep deterministic policy gradient,DDPG)算法作为仿生变形无人机的控制策略,可以使无人机在不同任务和飞行条件下完成快速的自主变形和空气动力学性能优化。王涛等[18]提出了一种基于强化学习方法暨模糊Q学习的多约束条件下自主导航控制算法,提高了复杂环境下无人机器人自主导航控制系统的自适应性和鲁棒性,通过对非完整性约束移动机器人运动模型的仿真,证明了该算法具有可移植性和通用性,可应用于无人机的空中躲避和拦截。Zhu等[19]以深度学习中的行动家-评论家(Actor-Critic)架构为基础,并结合预训练的ResNet网络,完成了无人机在离散3D环境中进行自主导航到达目的地的任务。
结合现有的研究成果进行分析可以发现,现有研究的不足有以下几点:
1) 大部分基于强化学习的无人机问题的研究都是针对静态任务展开的,且以DDPG为代表的智能算法具有学习和收敛速度慢,精度不高的缺陷。
2)相比于单架无人机,多无人机的相关问题研究过少。现在多数的多无人机协同任务决策依然使用DDPG算法[20],传统DDPG等智能算法在单架无人机相关领域表现优异,但是在多无人机环境下,由于涉及到的智能体数量多且复杂,收敛速度慢和精度不高的缺陷被放大,且随着无人机数量的增多,其适用能力下降。
2017年,多智能体深度确定性策略梯度(Multi-agent deep deterministic policy gradient,MADDPG)算法由OpenAI发表于NIPS,主要应用于多智能体的协同围捕、竞争[21-23]等场景,但MADDPG算法在多无人机协同任务决策作战应用中,特别是作战环境未知的情况下存在空白。为提高多无人机协同任务决策作战能力,本文提出了将深度强化学习中的MADDPG算法引入到多无人机系统中,设计一种能够符合多无人机系统特点的任务决策方法。
1 无人机任务决策与数学建模
1.1 任务决策分类
在解决多无人机任务决策问题时,首先要考虑战场环境的特殊背景。战场环境的多变性在一定程度上决定了任务决策的方法和难度。根据对战场环境的理解状况,可以将任务决策分为以下几种情况。任务决策分类如图1所示。
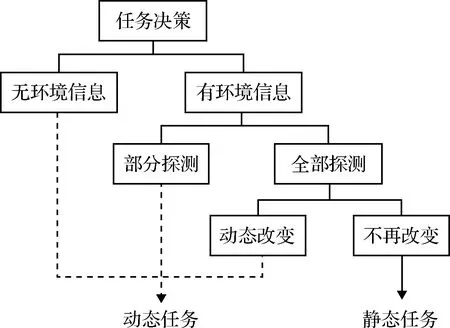
图1 任务决策分类Fig.1 Task decision classification
1)在开始任务之前已经掌握所有的战场环境。目标位置和战场中的防空雷达、防空导弹等一系列威胁区域均已被提前探测到,并且在无人机执行任务过程中不再发生改变,这一类战场情况对于无人机任务决策来说是最简单的,同时也是目前研究最为成熟的。只需要在任务开始执行之前,运用相关算法规划出最为合理且高效的航路,给无人机分配目标等任务信息,并加载给无人机,无人机就能够按照预定任务决策方案完成作战任务。
2)在任务开始前,只知道目标的位置,但是对作战区域的具体火力和威胁情况并未全部探测到或者只探测到一部分。这时就需要无人机一边执行任务一边进行探测,在执行任务的过程中对航路进行再规划,必要时对目标进行重分配。
3)还有一种情况更为复杂,目标区域的情况并未全部探测到,而且目标的位置也不是固定的,会随着时间移动。这是一种动态的战场环境,这种环境对无人机的智能化有着极高的挑战,需要无人机在复杂多变的环境中协同作战,动态实现规划航路以及目标任务分配,这也是最为复杂且最为困难的情况。
本文主要针对第二类情况做出任务决策,即目标和威胁源位置只进行一次初始化且均固定不变,作战区域的具体火力和威胁情况并未探测到。
1.2 无人机模型和威胁模型
1.2.1无人机建模
由于多无人机任务决策问题本身就具有高维度、高复杂性的特点,所以为简化研究问题,做出假设:认为多无人机为同构机型,具有相同的物理特性,并且在研究过程中不考虑无人机的形状大小等物理特性,将无人机简化为质心运动。则无人机质点在二维空间的简化运动模型定义为:
(1)

无人机在飞行过程中,由于惯性原因无法毫无约束的进行飞行转弯,在进行转弯飞行时会有一个最小转弯半径Rmin。如果航迹决策中的转弯半径Ruav小于无人机的最小转弯半径,则实际环境中无人机无法完成此动作决策。
1.2.2威胁建模
无人机在执行任务时,不但会遭遇来自地形和自然气候的威胁,而且还会遭遇来自敌方防空雷达、防空导弹等一系列防御措施的威胁,将这一系列对无人机安全能够造成危险的事物称为无人机威胁源。一般情况下,将无人机威胁分为自然威胁和军事威胁。本文在无人机攻击任务决策时,将环境因素理想化,忽略来自环境对无人机的威胁,主要考虑无人机的军事威胁,并且军事威胁以敌方雷达威胁和导弹威胁为主要威胁源。
雷达威胁主要是指无人机在敌方空域飞行时,能够探测并且对无人机造成影响的防空雷达。本文假设敌方防空雷达的探测范围是360度,在二维空间环境中等效为以雷达位置为中心,雷达水平方向探测最远距离Rmax为半径的圆周,定义为:
(2)
因此雷达威胁的数学模型为:
(3)
式中:UR是无人机当前位置与雷达位置的相对距离。
导弹威胁主要是指可以影响无人机正常飞行的防空导弹。和雷达威胁相同,导弹威胁在二维空间环境中也可以等效为圆周。但是不同的是,无人机与导弹的距离越近越容易被击中,无人机被击中的概率与无人机和导弹的距离成一定比例,因此导弹威胁数学模型如式(4)所示。
(4)
其中:UR是无人机当前位置与导弹位置的距离;dMmax为导弹所能攻击的最远距离,dMmin为导弹攻击允许的最近距离,一旦无人机与导弹的距离小于dMmin,则无人机一定会被击中。
无人机执行任务过程中,无论是静态任务还是动态任务都需要通过机载雷达设施对任务区域进行探测,以确定防空导弹等无人机威胁源的位置信息或者确保能够及时探测到突发威胁源的状况。这种探测行为可以更好的决策飞机的机动动作,规避危险,提高无人机的存活率。在无人机飞行探测过程中,将以机载雷达最大探测距离作为探测范围。
2 基于MADDPG的多无人机任务决策问题研究
2.1 DDPG算法
DDPG算法是Actor-Critic框架和DQN(Deep Q network)算法的结合体,解决了DQN算法收敛困难的问题。根据DDPG算法的特点可以将其分为D(Deep)和DPG(Deterministic policy gradient)两个部分。其中第一部分的D是指DDPG算法具有更深层次的网络结构,该算法继承了DQN中经验池和双层网络的结构,能够更有效的提高神经网络的学习效率。第二部分的DPG是指DDPG算法采用了确定性策略,Actor不再输出每个动作的概率,而是一个具体的动作。相比随机性策略,DPG大大减少了算法的采样数据量,提高了算法的效率,更有助于网络在连续动作空间中的学习。
DDPG算法从网络结构上来说应用了Actor-Critic的框架形式,所以具有两个网络:行动家(Actor)网络和评论家(Critic)网络。同时,Actor和Critic也都具备双网络结构,拥有各自的目标(Target)网络和估计(Eval)网络。DDPG的网络结构如图2所示。
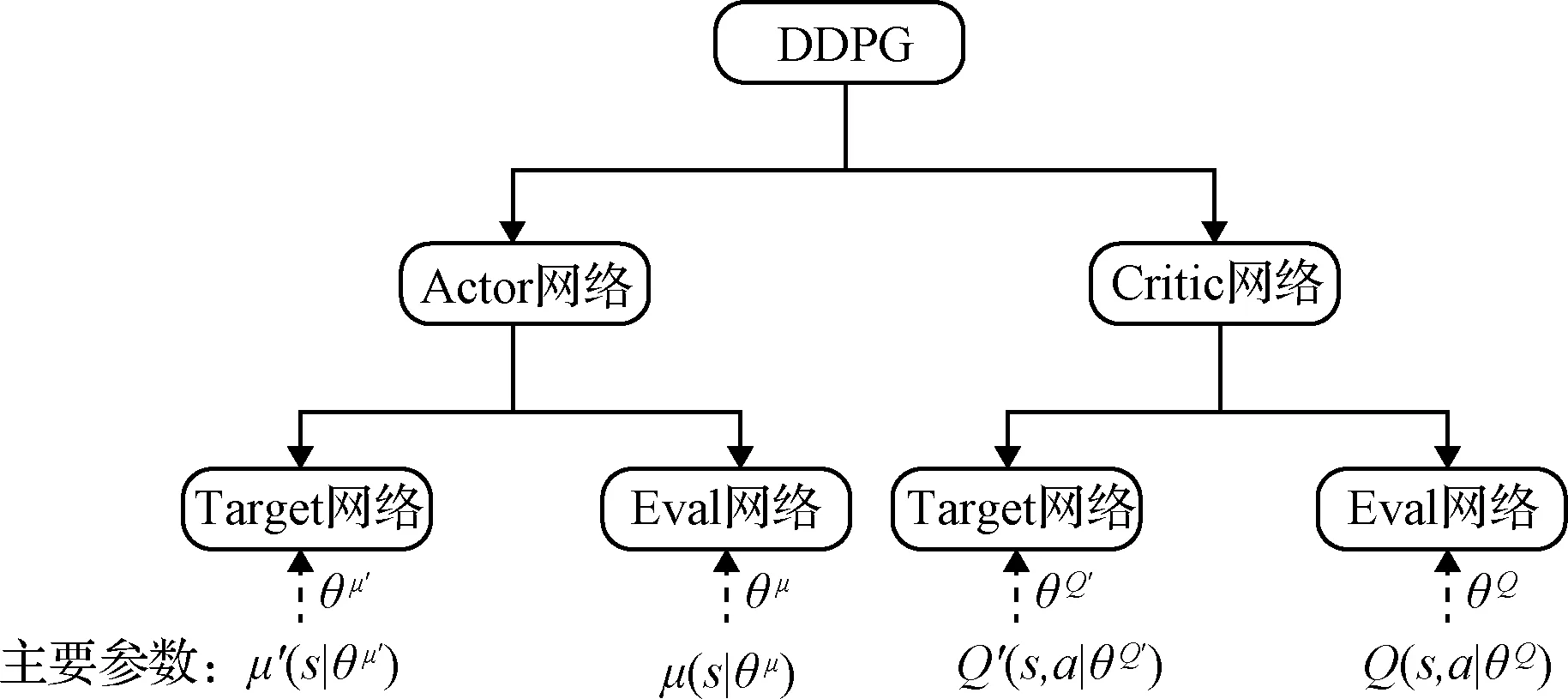
图2 DDPG的网络结构Fig.2 Network structure of DDPG
2.2 MADDPG算法模型
在多无人机的环境当中,传统的强化学习算法受到极大的挑战。在多无人机系统中每一个无人机都是独立的智能体,都需要不断的学习来达到改进其策略的目的。这样就导致从每一个无人机的角度来看,环境从静态转变为动态。这与传统强化学习收敛的条件大不相同,在一定程度上导致无法仅仅通过改变单个智能体自身的策略来适应不稳定的环境,并且传统策略梯度算法中方差大的问题会因为智能体数量的增多而被放大。而MADDPG算法就是针对这类问题而提出的一种基于多智能体环境的强化学习算法。
MADDPG算法基于Actor-Critic和DDPG进行了一系列的改进,并且采用集中式学习和分布式应用的原理,使其能够适用于传统强化学习算法无法处理的复杂多智能体环境。传统强化学习算法在学习和应用时都必须使用相同的信息数据,而MADDPG算法允许在学习时使用一些额外的信息(即全局信息),但是在应用决策的时候只使用局部信息。相对于传统Actor-Critic算法,MADDPG算法环境中共有M个智能体,第i个智能体的策略用πi表示,且其策略参数为θi,则可以得到M个智能体的策略集为π=π1,π2,…,πM,策略参数集合为θ=θ1,θ2,…,θM。第i个智能体的累计期望收益为:
(5)
其中:ri表示第i个智能体的奖励。
则针对随机策略,可以得到策略梯度公式为:
(6)

P(s′|s,a1,…,aM,π1,…,πM)=P(s′|s,a1,…,
aM)=P(s′|s,a1,…,aM,π′1,…,π′M)
(7)
同样可以将AC算法延伸到确定性策略μθi上,其回报期望梯度为:
(8)

(9)
其中,y由式(10)得到:
(10)
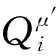

(11)
只要最小化上述代价函数,就能得到其他智能体策略的逼近。因此y可变为:
(12)
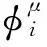
算法整体框架图如图3所示,根据算法整体框架图可知,针对单个智能体,首先将其状态输入到自身的策略网络当中,得到一个动作后输出并作用于环境中,此时会得到一个新的状态和回报值,最后将状态转移数据存入到智能体自身的经验池当中。所有智能体都会和环境进行不断的交互,不断的产生数据并存储到各自的经验池当中。
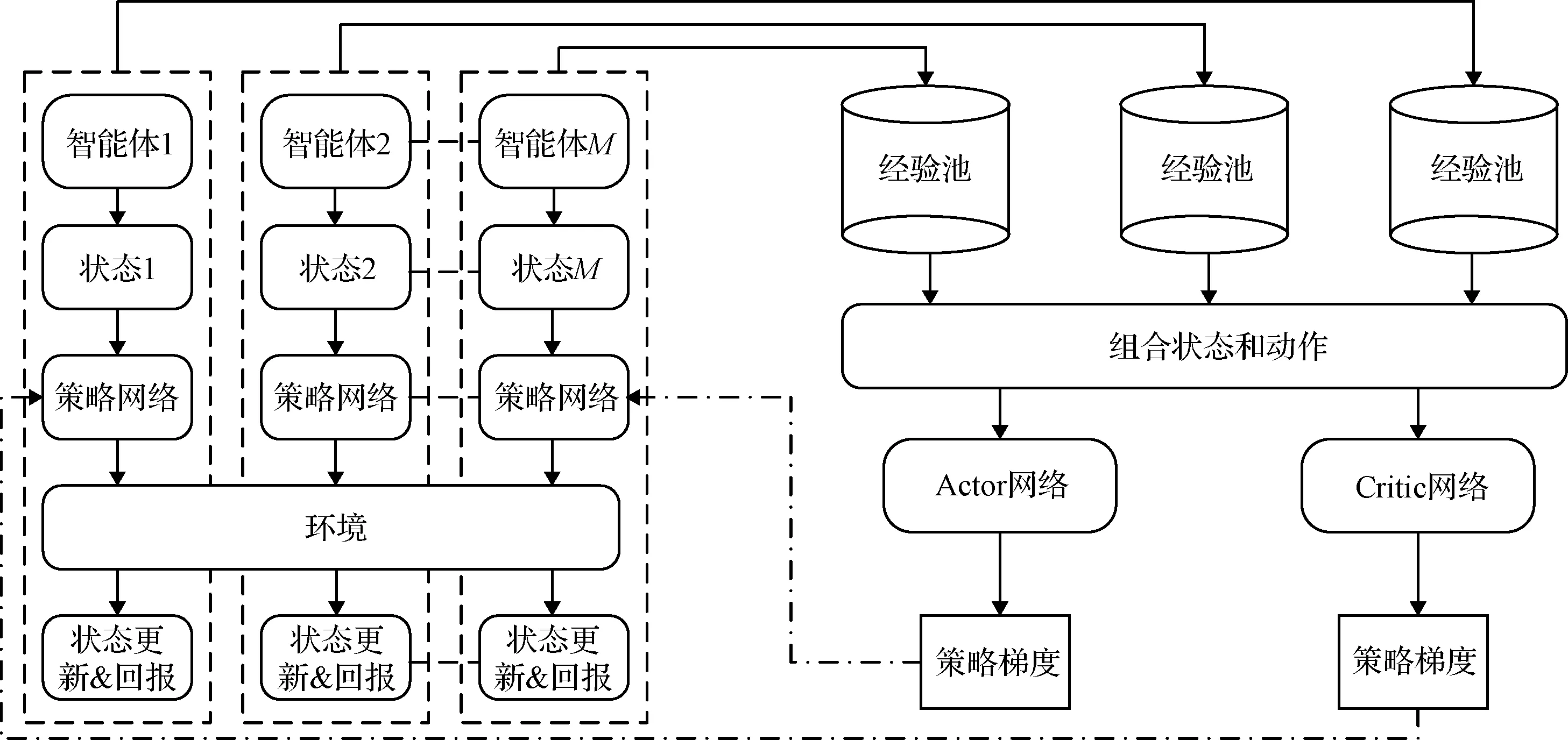
图3 MADDPG算法框架Fig.3 Algorithm framework of MADDPG
在更新网络的过程中,随机从每个智能体的经验池中取出同样时刻的一批数据,并将其拼接得到新的经验
yi=ri+γQ′(si+1,μ′(si+1|Qμ′)|θQ′)
(13)
实际的Q值通过使用评价网络得到,再利用TD偏差[24]来更新评价网络,用Q值的策略梯度来更新策略网络。所有智能体依照相同的方法来更新自身的网络,只是每一个智能体的输入有所差别,而在其它方面的更新流程相同。策略网络与价值网络的具体结构如图4所示。
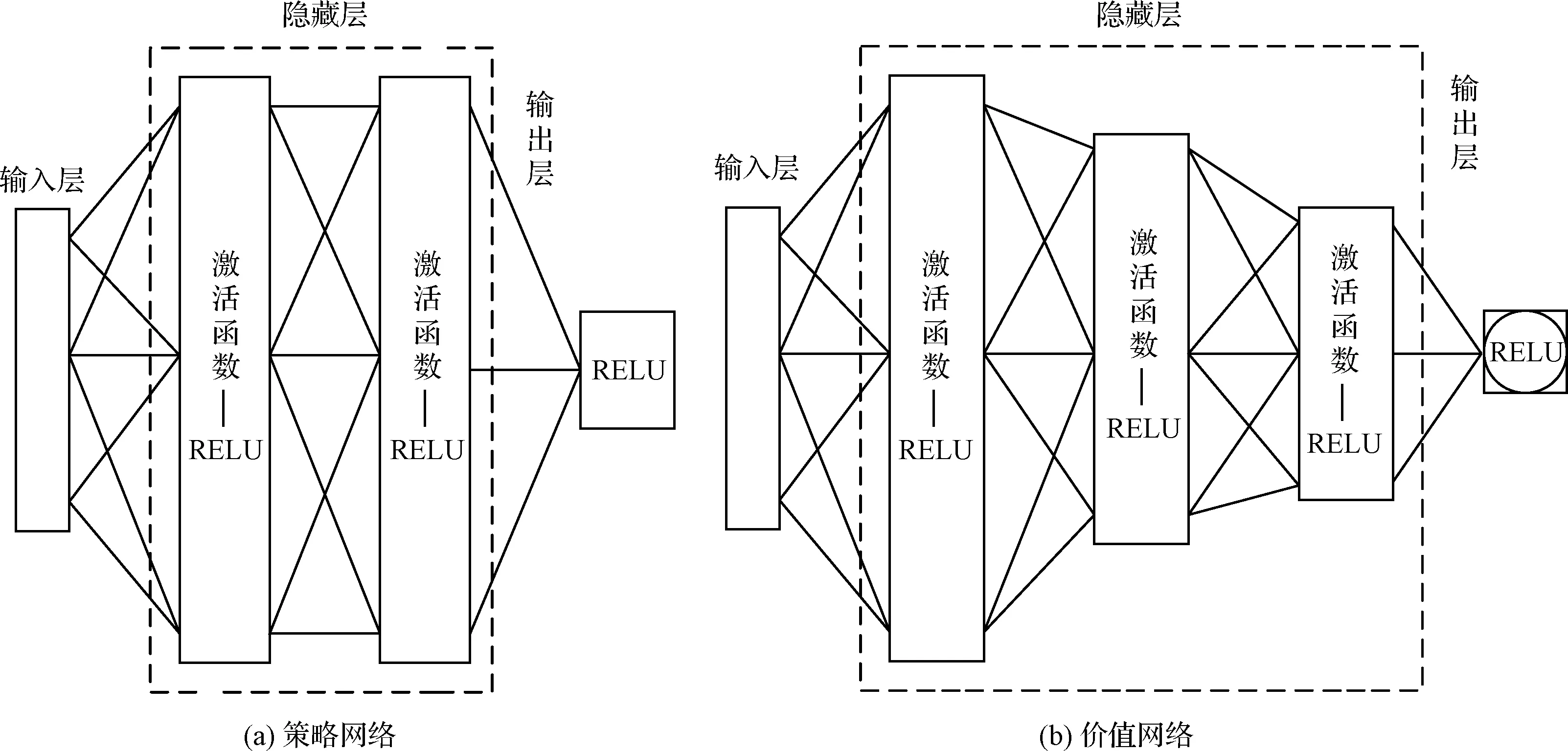
图4 网络结构Fig.4 Network structure
2.3 多无人机任务决策算法模型设计
本文主要基于二维平面环境开展研究,共有k架无人机分别为: UAV1,UAV2,…,UAVk。其中每一架无人机自身状态Suavi包含当前时刻的速度矢量(vuavi,x,vuavi,y)和在环境中的坐标位置(puavi,x,puavi,y)。环境状态Senv包含了环境中N个威胁区的坐标位置、威胁半径和M个目标的坐标位置。其中第i个威胁区的坐标位置和威胁半径分别表示为(Wi,x,Wi,y)和i,y,第i个目标在环境中的坐标位置可以表示为(Mi,x,Mi,y)。
在MADDPG算法中,每一架无人机的状态包括了自身的状态、其它无人机的状态和环境状态。针对无人机UAV1在t时刻的状态定义为:
St,uav1=(Suav1,Suav2,…,Suavk,Senv)
(14)
最终每架飞机在t时刻的状态定义为:
St,uavi=(vuav1,x,vuav1,y,puav1,x,puav1,y,…,
vuavk,x,vuavk,y,puavk,x,puavk,y,
Wi,x,Wi,y,i,y,Mi,x,Mi,y)
(15)
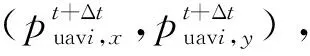
(16)
并且,无人机的动作输出,受到最小转弯半径的约束,如果不符合约束条件,则被视为不合理动作输出,需要进行重新选择。
本文主要从以下三个方面来设计奖励函数。
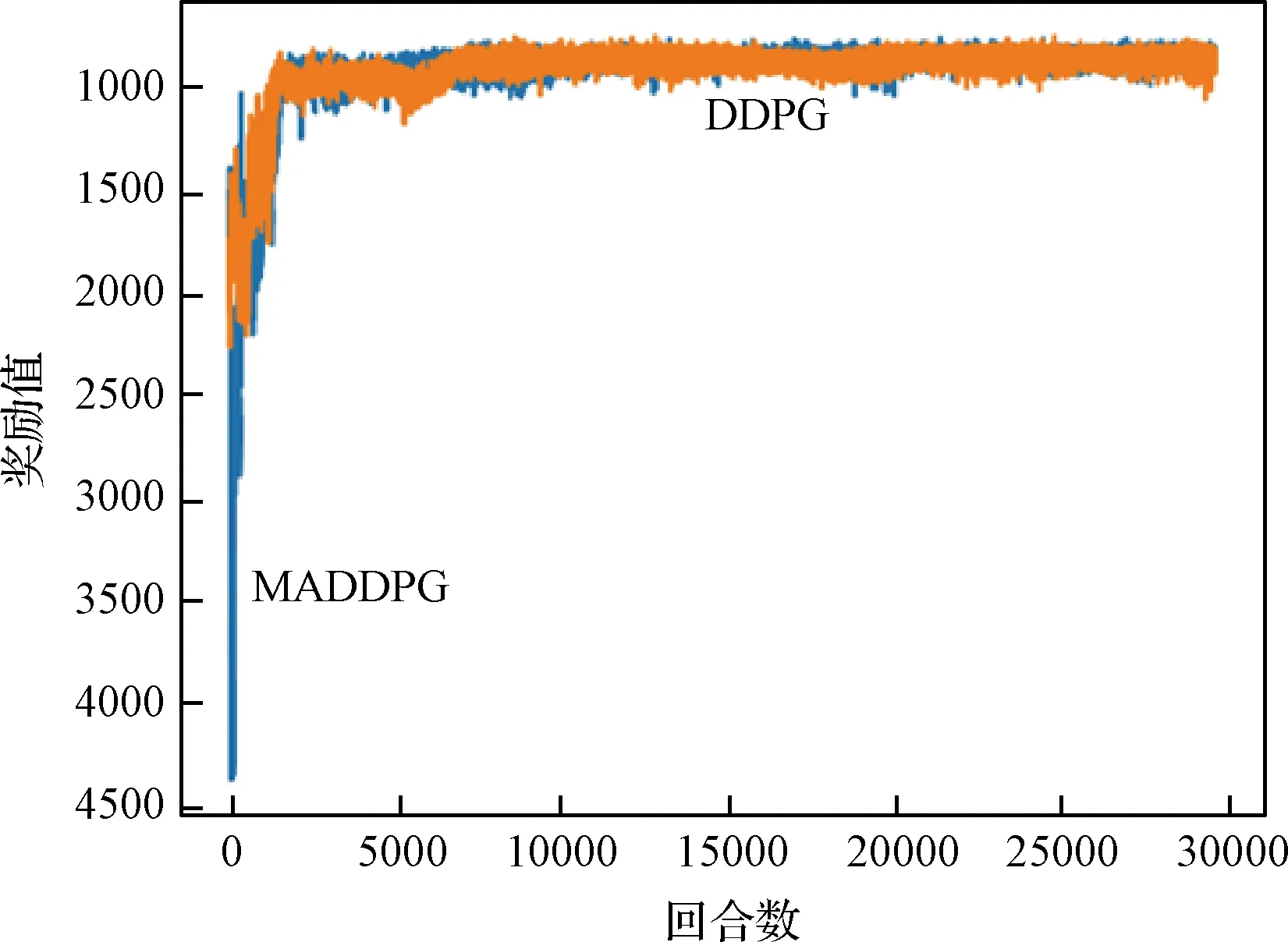
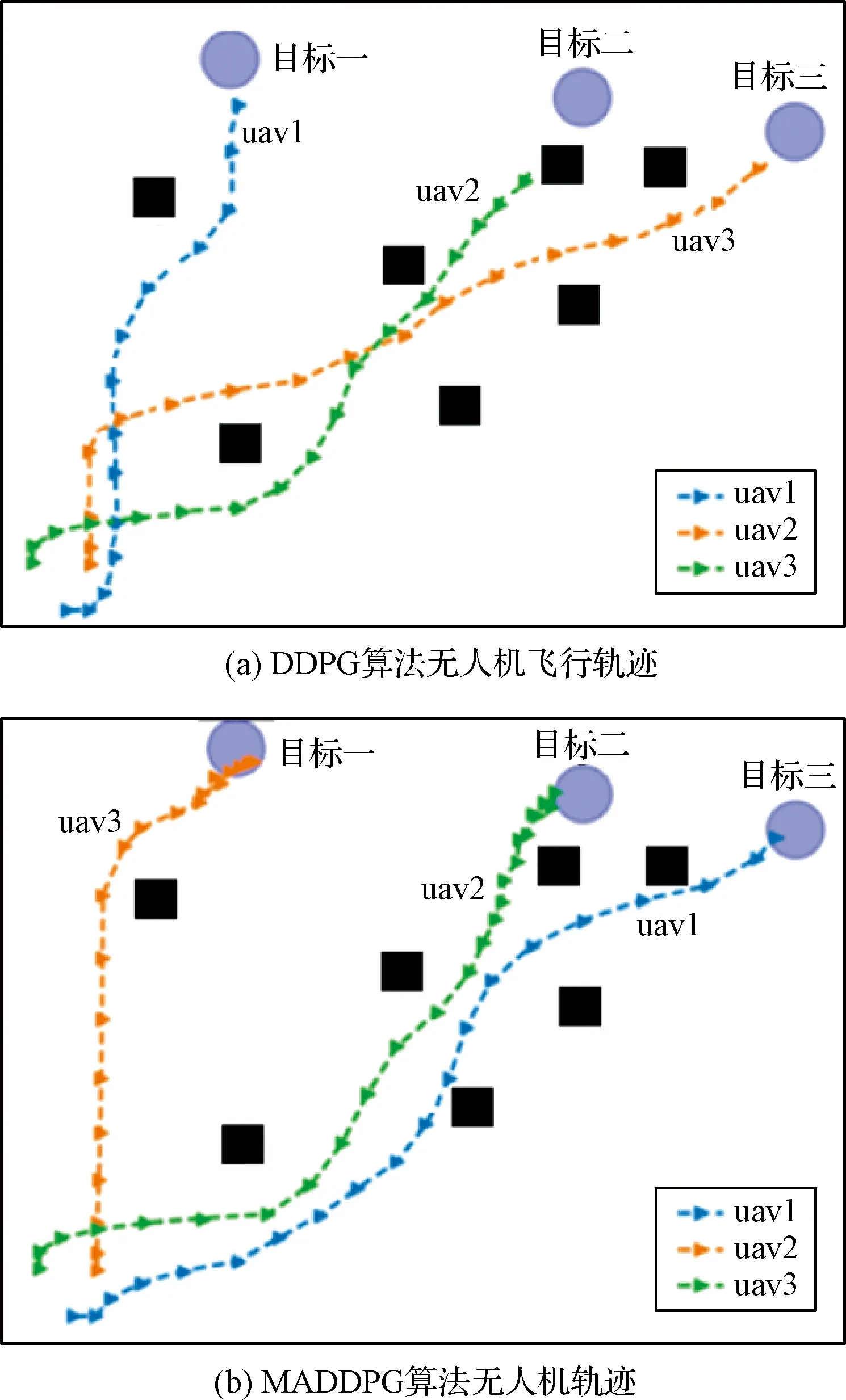
1)针对躲避威胁区设定一个威胁奖励,当无人机进入威胁区后,会被给予一个负奖励。即Rf=-1,(DW 2)在无人机的飞行过程中,每一架无人机都应和其它无人机保持安全距离,一旦无人机的位置过近,就会互相产生飞行威胁甚至发生碰撞,所以为了避免无人机发生碰撞,应当设定一个碰撞奖励Rp,当无人机间的距离小于安全距离时,就会给予其负奖励。即Rp=-1,(Ddij 3)为了在开始训练时,能够准确的引导无人机的动作选择,并且让无人机每一步都拥有一个密集奖励,在这里设计了一个距离奖励Rr,计算每一时刻,无人机与目标的最近距离,以距离的负值作为奖励值,距离越近,奖励值越大。即Rr=-dmin,其中dmin是各个目标和各架无人机之间最小距离的和。 最终无人机的奖励函数设计为: Ri=Rf+Rp+Rr (17) 本文设计了MADDPG算法模型,采用了确定性动作策略,即a=πθ(s)。网络结构设计为:策略网络结构为[39;56;56;2]的全连接神经网络;价值网络的结构是[123;118;78;36;1]的全连接神经网络,神经网络隐藏层都采用RELU函数作为激活函数,网络结构表示输入层、隐藏层和输出层对应的节点数。在训练时的mini-batch大小为1024,最大回合数(max episode)为30000,辅助网络的更新率0.01,价值网络的学习率为0.01,策略网络的学习率为0.001,两个网络都采用了Adam Optimizer优化器进行学习,经验池的大小为1×106,一旦经验池的数据超过最大数值,将会丢掉原始的经验数据。 表1 MADDPG网络结构参数Table 1 Network structure parameters of MADDPG 初始化仿真环境包含三架无人机的初始位置、三个目标的位置和7个威胁区的分布情况。具体初始环境如图5所示。 图5 初始环境Fig.5 Initial environment 通过建立DDPG和MADDPG两种模型结构进行训练。最终得到奖励函数如图6所示。 图6为训练过程中,三架无人机在每一回合(episode)训练时的奖励变化图。横坐标表示训练的回合数(episodes),纵坐标表示每一回合训练时三架无人机的累计奖励。可以看出随着训练次数的增多,奖励的绝对值减小,但是奖励逐渐增大,由于训练过程中存在随机噪声,所以训练时无论是哪个时刻都存在振荡现象,但从图6中依然可以看出,在训练回合数达到10000回合后,两种算法的奖励曲线趋于平缓,总体呈收敛趋势。 图6 训练奖励收敛曲线Fig.6 Reward convergence curve of single step training 图7是三架无人机网络参数变化曲线图,表示每架无人机网络结构中Actor网络和Critic网络的Q值(状态动作值)和损失值(Q估计值和Q实际值之间差距的平方)的变化规律。图7(a)是DDPG算法模型三架无人机网络参数的变化曲线图,图7(b)是MADDPG算法模型三架无人机网络参数的变化曲线图。可以看出,两种算法随着训练次数的增加,Actor网络的Q值逐渐增大,直到收敛。Critic网络中损失值随着训练的次数增加而逐渐减少,直到收敛。对比DDPG和MADDPG两种算法中每架无人机网络Q值和损失值的变化曲线,可以发现DDPG算法在训练过程中,每架无人机网络的Q值在训练到5000回合之后有明显的下降趋势,而MADDPG算法整体呈上升收敛趋势,没有明显的波动变化趋势。且MADDPG算法中每架无人机网络的初始损失值明显小于DDPG算法中的初始损失值,而且在两种算法收敛后,MADDPG算法中的损失值要明显小于DDPG算法中的损失值。说明了MADDPG比DDPG算法具有更强的稳定性和更快的收敛性。最终两种算法模型的轨迹图如图8所示。 图7 不同算法无人机网络参数变化Fig.7 Changes of UAV network parameters based on different algorithms 图8(a)为DDPG算法模型经过训练后得到的无人机轨迹图。图8(b)为MADDPG算法模型训练后得到的无人机轨迹图。对比两种算法模型的无人机飞行轨迹可以看出,DDPG算法最终的飞行轨迹 图8 不同算流下的无人机轨迹Fig.8 Flight path of UAV based on different algorithms 并没有完全进入目标区域,相对目标有一定的距离,而且第二架无人机的轨迹还进入了威胁区内。而MADDPG算法模型的飞行轨迹全都进入了目标区域,而且躲避了所有的威胁区。综合分析两种算法的奖励曲线变化图和飞行轨迹图,可以得出结论:在该环境下,MADDPG算法优于DDPG算法。 针对现有多无人机任务决策研究中的缺点,进行了基于MADDPG算法的多无人机任务决策问题的研究,详细阐述了MADDPG算法的原理和特点,并且基于多无人机任务背景,分别从网络结构、状态空间、动作空间和奖励函数设计了MADDPG算法的模型结构,将MADDPG算法和多无人机任务决策问题相结合,实验证明MADDPG算法不仅可以解决多无人机任务决策问题,并且相对DDPG算法,针对传统算法学习效率并不高的缺陷,本文提出的方法具有更快的收敛速度和学习效率。3 实验及分析
3.1 参数设计

3.2 结果分析


4 结束语

