行星着陆轨迹优化技术研究进展

崔平远，龙嘉腾，朱圣英，修文博

(1. 北京理工大学宇航学院，北京 100081；2. 深空自主导航与控制工信部重点实验室，北京 100081；3. 飞行器动力学与控制教育部重点实验室，北京 100081)

0 引 言

近年来，火星探测和小天体探测成为地外天体探测的热点领域。火星是太阳系中与地球环境最为相似的行星，是研究生命起源的理想目标[1]；小天体种类丰富，数量繁多，保留了大量太阳系形成早期的原始物质，加之复杂的动力学环境，具有重要的科学研究价值[2-6]。

随着探测活动的深入以及探测手段的进步，在地外目标天体高科学价值区域开展原位探测和采样返回成为未来行星探测的重要发展方向。在地外天体表面实施精确、安全着陆是实现上述探测任务的关键。以美国“火星科学实验室/好奇号”任务[7]和日本“隼鸟号(Hayabusa)”探测任务[3]为代表，自主导航、制导与控制技术是实现地外天体表面精确着陆的关键技术。2014年，欧洲空间局“罗塞塔/菲莱(Rosetta/Philae)”[4]探测任务中，探测器由于弹跳至彗星阴影区而难以正常开展探测工作，凸显了高精度控制在小天体着陆任务中的重要作用[8]。从上述行星着陆任务分析表明，高精度制导与控制是实现地外行星表面高精度着陆的重要技术发展趋势[9]。

着陆轨迹优化是行星着陆探测任务分析、制导与控制系统设计的重要技术基础。通过设计性能指标、施加约束条件，进行着陆轨迹优化是分析着陆轨迹特性、研究约束条件和着陆环境因素影响的重要途径，进而为着陆总体方案优化、着陆点选取、制导与控制算法设计提供依据。此外，轨迹优化方法也是在现有技术条件下，扩展地外天体探测能力的重要途径。例如在火星着陆过程中，通过对大气进入段的末端飞行高度进行优化，可以显著提高探测器最终的着陆高度范围，进而显著扩大探测器的可能探测区域。行星着陆轨迹优化是基于动力学模型，通过数值优化的方法，寻找满足一定约束条件并使性能指标达到最优的飞行轨迹。近年来，国内外学者针对不同行星着陆背景、技术条件和任务需求，对行星着陆轨迹优化问题开展了大量的深入研究工作。相关研究成果在揭示行星着陆轨迹特性，提高轨迹优化算法的收敛性、快速性和精确性等方面具有重要的实践意义。

本文通过总结近年来行星着陆轨迹优化领域的研究成果，结合行星着陆制动方式，对着陆探测轨迹优化问题特点和研究现状进行梳理。在此基础上，总结归纳出行星探测轨迹优化的关键技术及发展趋势。

图1 小天体着陆探测任务目标天体Fig.1 Objects of small body landing exploration mission

1 着陆轨迹优化的特点

根据行星环境的不同，行星着陆的制动方式主要分为大气制动和动力制动。大气制动着陆方式用于具有大气层的行星及其卫星(如地球、金星、火星、土卫六等)着陆过程，是以飞行器气动阻力作为主要制动力来源，通过设计合理的飞行器气动外形来产生足够的气动制动阻力，并在飞行过程中调整飞行器姿态改变气动力方向达到调整飞行轨迹的目的。依据飞行器在高超速段升阻比的不同，大气进入飞行器可分为低升阻比飞行器(升阻比为0.3左右，如阿波罗任务返回舱、猎户座任务返回舱、MSL任务进入飞行器等)、中升阻比飞行器(升阻比为0.5～0.9左右，如CobraMRV火星探测器、X-33飞行器等)和高升阻比飞行器(升阻比大于1.5，如航天飞机、CAV-H高超声速飞行器等)。

动力制动着陆方式主要适用于没有大气的行星及其卫星(如月球、小天体)着陆过程，或作为大气制动的一种辅助接续制动方式(如火星着陆)，是以反推发动机推力作为主要减速制动力，通过改变推力大小和方向实现对着陆轨迹的调节。这种着陆方式主要应用于月球着陆、火星动力下降段、重复运载火箭着陆回收、小天体软着陆等着陆任务中。值得注意的是，在月球、火星、地球等类球形天体表面附近采用动力制动着陆时，通常考虑常值引力作用；而小天体动力制动着陆过程中，不规则引力作用随探测器位置呈现出复杂时变非线性特征。

结合行星环境，在现有技术水平下，火星着陆主要采用大气制动减速并辅之以动力制动减速，小天体着陆采用动力制动减速。下面结合两种制动方式在着陆动力学形式、约束构成、不确定因素来源等方面的特点，分析着陆轨迹优化所面临的技术挑战。

1.1 动力学呈现强非线性

在着陆过程中，除自身控制力作用外，探测器所受外力作用主要包含气动力作用(大气进入过程)、引力作用、惯性力作用。在不同的着陆背景中，探测器受上述各种外力作用的影响程度各不相同。

稳定的大气层仅存在于引力较强的行星(及其卫星，如土卫六)周围。在行星大气进入过程中，气动力作用和引力作用对探测器动力学均具有较强的影响作用。其中，类球形引力场中的引力作用较为规则，而气动力作用则十分复杂，与探测器气动外形、飞行姿态、大气密度等因素密切相关[10]。同时，气动力与飞行速度、飞行高度等飞行状态呈现复杂的非线性特征。同时，大气进入过程采用调整姿态改变飞行器运动轨迹的控制方式，进而导致控制力与动力学之间的传递关系呈现高度非线性。

与此对应，由于小天体质量小、引力弱，难以吸引足够的气体分子形成稳定的大气层。因此在小天体软着陆过程中，探测器主要受到引力作用和惯性力作用。同时，小天体的微弱引力难以使其聚合成类球体，使小天体三维形状和引力场空间分布极不规则。在不规则引力场环境下，引力势与探测器位置呈现高度复杂的非线性特征。这种非线性特征导致探测器受空间扰动(如太阳光压、第三体引力摄动等)的影响更为显著[11]。此外，小天体自旋状态复杂，存在超快自旋、极慢自旋乃至非主轴自旋等情形，更加剧了探测器动力学的复杂程度[8]。

1.2 着陆过程存在复杂约束条件

为保证着陆精确性和安全性，探测器着陆轨迹需满足复杂的约束条件。这些约束条件可大致分为路径约束和末端约束。其中，路径约束主要是保障飞行过程中的安全性，末端约束主要是依据任务需要，保障着陆的精确性。在不同的着陆背景下，上述约束条件的构成要素也不尽相同。

大气制动过程通过借助气动阻力(摩擦阻力、激波阻力等)完成飞行器减速。从本质上讲，大气进入过程中，飞行器初始机械能转化为气动热进行耗散实现减速。因此，即使火星大气密度十分稀薄，火星大气进入过程中也同样会产生显著的气动热[12]。同时，随着飞行高度的降低，行星大气密度呈指数形式增大，探测器因而受到巨大的气动过载。为保证飞行安全，需对气动吸热和气动过载加以约束。气动吸热因素主要考虑的约束条件有热流峰值和总吸热量约束。此外，考虑任务需要，在一些大气进入过程中还需考虑路径点约束和禁飞区约束等[13]。

以动力制动为主要减速方式的行星动力下降和小天体软着陆过程中，引力作用是主要考虑的外力作用。动力制动过程中，以发动机反推作用实现制动减速，为防止控制力饱和，轨迹优化中需考虑推力器控制力的幅值约束；为保障飞行安全，避免目标天体表面发生碰撞，需引入障碍规避约束[14-15]、最小飞行高度约束、滑翔角约束；为保障导航相机对目标着陆点的可见性，需考虑相机视场角约束。

上述行星着陆复杂约束条件的共同作用将直接影响到着陆轨迹可行域，进而对轨迹优化方法的收敛性产生影响。

1.3 着陆环境不确定性显著

由于近地空间附近存在大量人类活动，诸如大气环境、引力场环境等空间环境信息已得到系统、深入、精确的建模。与此对应，人类对地外天体环境知之甚少，绝大多数小天体探测都是首次开展。在探测过程中，受观测和探测手段的限制，无法全面、准确地掌握目标地外天体的大气环境、地形环境、引力环境等环境要素。因而在着陆过程中，着陆环境的不确定性显著，进而影响着陆精确性和安全性。

在大气进入过程中，大气固有属性(大气组分、大气密度等)和探测器气动外形是决定探测器气动力作用的两个重要方面。因此，行星大气进入过程中存在如下不确定因素：

1)不同行星的大气组分、大气密度各不相同，且大气活动随季节变化现象显著。作为气动减速介质，行星大气的精确建模难度极大。以火星大气为例，火星大气密度十分稀薄，仅为地球大气密度的1%(如图2所示)，不确定性随飞行高度变化显著(如图3所示)，且时常伴有阵风等不确定因素。因此，火星大气模型的不确定性是大气进入过程中的重要不确定因素来源。

图2 火星与地球大气密度对比Fig.2 Comparisons of the atmosphere density of the Mars and the Earth

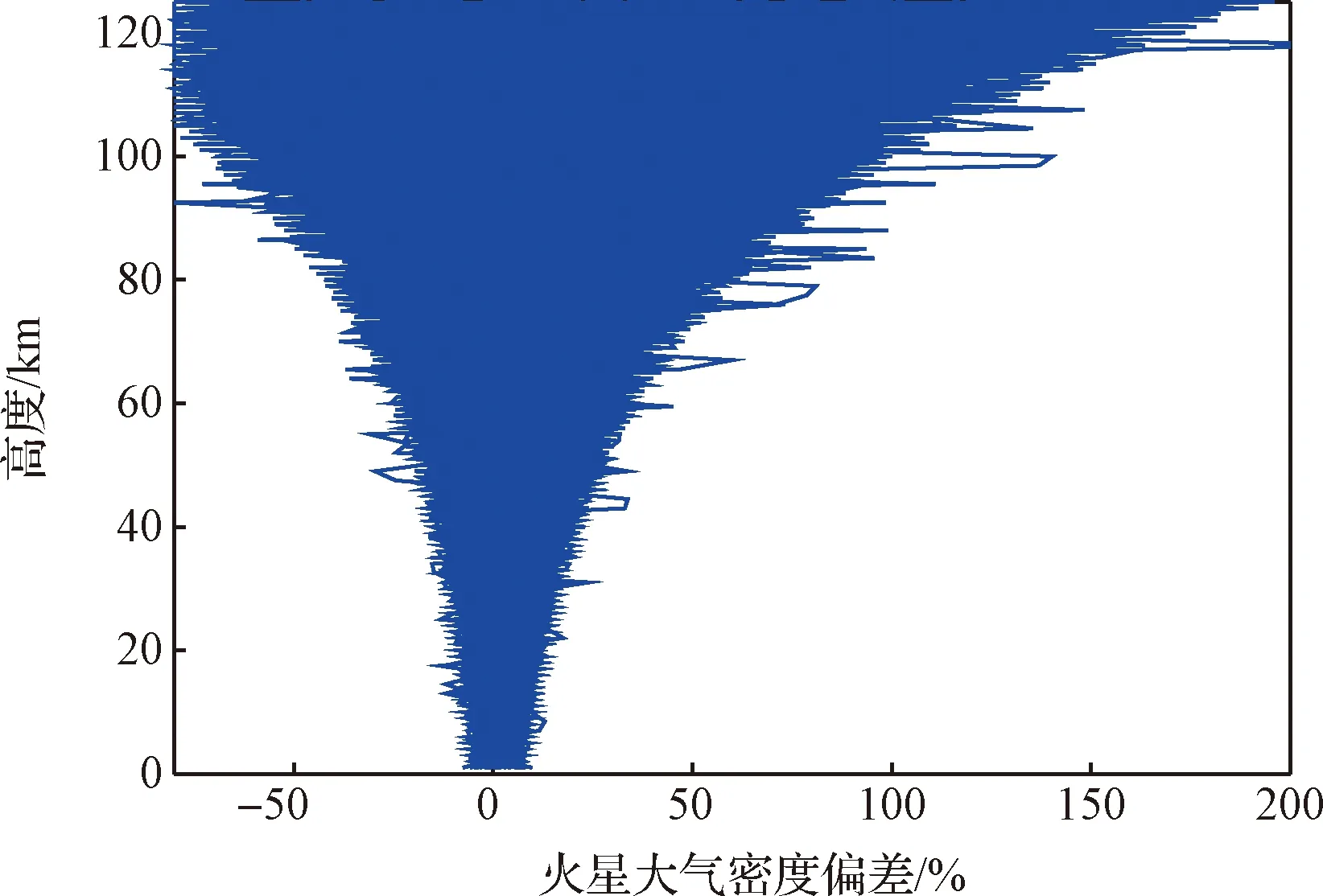
图3 火星大气密度偏差随高度的分布情况[17, 21]Fig.3 Distribution of the mars atmosphere density bias with respect to altitude[17, 21]

火星大气建模需考虑高度、经纬度、季节、理化性质等多种因素，目前较为完备的火星全球大气数据库有欧空局的火星气候数据库(Mars climate database，MCD)[16]和美国的火星全球参考大气模型(Mars global reference atmospheric model，Mars GRAM)[17]。在实际研究中，常用的火星大气简化模型为指数模型和分层指数模型[18]等。火星大气密度指数模型给出了大气密度随飞行高度的解析表达形式，便于开展理论研究工作，且形式简洁、解算效率高。但简化指数模型在高空处对大气密度的拟合精度较高，而在接近火星表面处存在较大的偏差。

2)气动力作用引起的气动弹性、气动烧蚀效应引入较大不确定因素。行星大气进入过程中，飞行器所受气动力作用导致飞行器弹性形变，使得气动外形产生微弱变化，进而导致气动力作用的改变。因而气动力与气动力外形间呈现复杂的气动弹性耦合效应。与此同时，即便在探测器设计承受范围之内，气动加热效应对探测器气动外形的改变，进而对气动力造成的不确定性效应依然不可忽略。在行星大气进入三自由度动力学中，这种不确定性效应主要体现在探测器升阻比和弹道系数的不确定性[19]。因此，以末端高度为性能指标进行轨迹优化并设计相应最优制导策略是火星大气进入轨迹设计的重要方面[20]。

在动力制动着陆过程中，行星表面形貌的不确定性对探测器着陆安全构成极大威胁。行星表面存在大量诸如陨石坑、巨石、斜坡、裂谷等复杂形貌。这些表面形貌特征一方面可作为天然导航路标，提供丰富的图像导航特征[22]；另一方面，也在行星着陆过程中成为表面障碍，严重威胁到探测器安全[14-15]。小天体表面无大气风化等理化侵蚀作用影响，保存着大量小天体形成初期即已存在的复杂表面形貌。这些表面形貌类型众多，特征尺度千差万别，为建模带来极大困难。

图4 地外行星表面崎岖Fig.4 Hazardous object surface

在小天体动力制动着陆过程中，小天体不规则引力场是主要的不确定因素来源之一。小天体质量和体积微小，所形成的微弱引力不足以将其凝聚为类球形天体。由此导致小天体形状和引力场极不规则，引力场在各个方向上呈现出显著的各向异性。目前小天体引力场模型依赖大量观测数据，在算法精度和解算效率上无法得到有效兼顾。加之小天体质量分布不均匀，不规则引力场模型不可避免地引入建模误差。此外，由于小天体引力场微弱，导致探测器受到的第三体引力摄动有时变得不可忽略。同时，小天体附近不存在大气，不存在对太阳光的显著散射现象，因此，太阳光压摄动也是探测器在小天体着陆过程中所需考虑的摄动源[23]。

2 着陆轨迹优化研究现状

传统轨迹优化方法[24]分为间接法和直接法。间接法利用极小值原理，通过拉格朗日乘子法引入协态变量来求解最优控制问题。其优点在于求解精度高，但同时也存在初值猜测敏感这一显著缺点，导致求解收敛域很小。由于协态变量没有明确的物理含义，其初值难以获得[20]。针对间接法的初值猜测敏感问题，同伦法[25-26]是一种行之有效的解决方法。直接法是将着陆轨迹优化问题转化为多种路径约束和边界约束下的静态参数优化问题，进而采用非线性规划算法进行求解，但易陷入局部最优。由于实现方便，直接法在工程实践中被广泛采用。下面针对不同行星着陆背景，对相应轨迹优化方法的研究现状进行分析。

2.1 非线性动力学环境下着陆轨迹优化研究现状

行星着陆过程中，探测器处于极为复杂的非线性动力学环境中。根据行星环境和制动方式的不同，动力学的非线性来源也不相同。需要指出的是，行星着陆的非线性动力学环境对着陆轨迹优化算法的精确性和收敛性提出了较高要求，同时也导致相关飞行特征参数对着陆轨迹产生重要影响，进而决定着轨迹优化性能指标的选取。

大气制动着陆的动力学环境极为复杂，其强非线性特征主要来源于以下两个方面：1)大气密度与飞行高度间的非线性关系；2)气动力与大气密度、飞行速度、飞行高度间的非线性关系。这种强非线性关系，导致着陆飞行轨迹受飞行参数的影响显著。例如在火星大气进入过程中，最大末端飞行高度与气动参数(弹道系数、升阻比)存在密切关系。目前火星大气进入段轨迹优化问题中，以小升阻比航天器飞行轨迹作为主要研究和设计对象。由于小升阻比飞行器所产生的气动升力有限，加之火星大气密度稀薄，提高进入段末端高度[20, 27, 28]成为火星大气进入轨迹优化问题的重要优化目标。文献[20]从理论上证明了在标称条件下，使末端高度的最优倾侧角剖面满足bang-bang控制形式，将传统的多节点进入段轨迹优化问题转化为对bang-bang控制切换时刻的搜索问题，显著降低了进入段轨迹优化的复杂度。

动力制动着陆过程中的动力学非线性因素主要包含控制推力幅值的饱和约束[29]以及小天体的不规则引力影响[30]。由于动力制动着陆方式通过消耗反推发动机燃料进行减速，着陆轨迹及控制方式所对应的燃耗是分析任务可行性和安全性所需考虑的重要因素，因而燃耗最优问题广泛存在于月球着陆[31]、火星着陆[32]、小天体软着陆[30]等航天各类任务中。此外，相关文献深入研究了动力制动着陆方式的时间最优问题[33-34]、能量最优问题[35]和脱敏最优问题[36]等。不同性能指标对优化问题复杂程度各不相同，文献[35]研究了小天体软着陆过程中的燃耗最优与能量最优问题间的内在联系，并采用快速同伦法通过求解着陆能量最优问题获得燃耗最优问题的解。同伦法的问题在于，无法构建多种优化问题间的普遍联系，因此适用范围收到限制。针对小天体不规则弱引力场所导致的动力学非线性问题，文献[37]在采用凸优化求解的过程中，采用局部线性化方法，对非线性动力学进行凸化处理。该方法有效解决了非线性非凸动力学条件下的凸优化解算问题，但需考虑解算过程中的节点选取和非线性动力学近似所引入的解算偏差。

针对行星着陆的强非线性动力学环境，在着陆轨迹优化过程中，采用相应的轨迹拟合和逼近方法是处理非线性动力学问题的有效手段，包括局部逼近技术和全局逼近技术。

局部逼近技术是以某个物理参量(通常为飞行时间或随飞行时间单调变化的独立变量)为依据，对整个飞行过程按一定间隔进行区间划分得到若干节点，在各个区间上对飞行轨迹进行分段局部逼近。局部线性化技术是一种经典的局部逼近方法。传统直接法中的直接打靶法和直接配点法也属于局部逼近的范畴由于局部逼近技术是对着陆轨迹进行分段逼近，在精确性和求解效率方面存在一定不足。

近年来，以伪谱法[38-39]为代表的全局逼近技术得到了广泛研究。伪谱法又称为正交配点法，采用高阶正交多项式的根作为配点，以对应正交多项式作为基函数，同时离散状态变量和控制便令，对着陆轨迹进行逼近，将着陆动力学微分约束转化为代数约束。研究表明，伪谱法对光滑问题具有良好的收敛性，且Gauss伪谱法的KKT条件等价于极小值原理的一阶最优性条件[38]。在大气进入[40-41]、动力下降[42]、小天体软着陆[43]轨迹优化中得到了成功应用。伪谱法的缺点在于节点数量的选取由于没有明确的规则而过多依赖于设计者的经验。采用高阶多项式在固定节点和配点处拟合状态变量和控制变量。若系统包含不连续或者曲率较大的状态/控制变量时，需增加节点数目以保证逼近精度，从而导致整个算法的计算效率下降。同时，由于行星着陆轨迹优化存在大量复杂约束，加之动力学强非线性，且传统直接法轨迹优化解算结果没有一阶必要性条件保证，解算过程易陷入局部最优，对优化初值的选取有较高要求。因此，在高度复杂的非线性着陆动力学背景下，如何采用全局逼近技术对着陆轨迹进行精确逼近，并寻找合理转化方法，保证求解问题的等价性和最优性，是处理着陆非线性问题的有效途径。

2.2 复杂着陆轨迹约束下着陆轨迹优化研究现状

综合考虑飞行器安全、着陆精确性、飞行器控制能力等因素，行星着陆轨迹优化需引入路径约束、边界条件约束和控制约束等复杂约束条件。这些约束条件显著影响轨迹优化问题的可行域，进而影响轨迹优化算法的收敛性。

传统轨迹优化方法通常将复杂约束条件转化为不等式约束(路径约束)或等式约束(边界条件约束)，进而通过罚函数法[40]、拉格朗日乘子法[30]等方法进行求解。这些方法在处理不同约束条件时具备较好的通用性和适应性，获得了广泛的应用。但在大量非线性约束条件的共同作用将导致轨迹优化问题的可行域极为复杂，进而对轨迹优化算法的收敛性和精确性带来显著影响。

近年来相关研究成果表明，采用凸优化方法求解复杂约束条件下着陆轨迹优化问题时，在求解精度和计算效率方面具有明显优势，受到了国内外学者的广泛关注。尤其是内点法在求解凸优化问题时能够在多项式时间内，以给定精度完成问题的求解[44]，并成功应用于不同航天任务背景的轨迹优化与制导算法设计问题[29, 37, 45-46]。文献[15]综合动力下降过程中的燃料消耗、避障约束、着陆视场角约束等多种因素，依据着陆动力学，通过分析动力下降轨迹特性，设计出满足避障约束的着陆凸轨迹。针对行星着陆过程中复杂约束条件下的轨迹优化问题，“矢量轨迹”方法[47]通过轨迹的矢量描述、约束的矢量表达、规划的矢量求解，将非凸几何约束着陆轨迹优化问题，转化为二阶锥规划问题实现快速求解。针对小天体着陆过程中存在的非线性动力学以及复杂非凸约束(路径约束和边界约束)，文献[29]通过将动力学线性化、变量代换和变量松弛技术，将小天体着陆问题转化为二阶锥规划问题进行求解，显著提高了轨迹优化问题的解算效率和求解精度。

采用凸优化方法进行着陆轨迹优化时，通常将包含状态的非凸路径不等式约束通过局部泰勒展开转化为线性不等式约束或者二阶锥约束[46]，而对非凸控制约束采用变量松弛方法加以转化。非凸控制约束通常可描述为

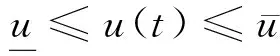
(1)

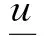
图5 大气制动控制变量的松弛方法[46]Fig.5 Control variable slack method for atmospheric entry[46]

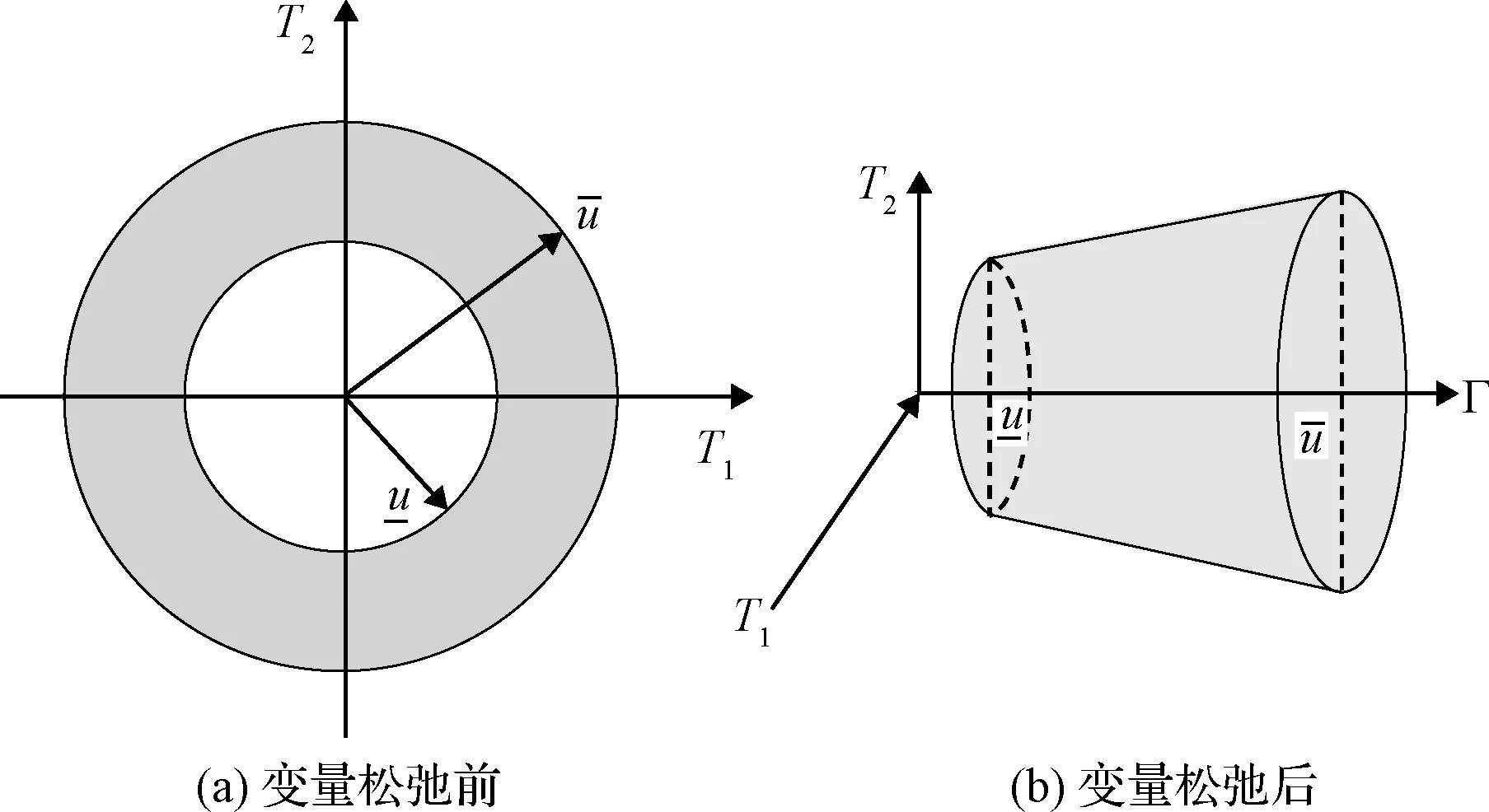
图6 动力制动控制变量的松弛方法[34]Fig.6 Control variable slack method for powered descent landing

行星着陆中存在大量状态耦合约束。状态变量的迭代更新将导致上述状态耦合约束的改变，进而反作用于轨迹优化的状态迭代更新。因此，存在状态耦合约束的优化问题中，需采用序列优化求解技术。在行星着陆轨迹优化问题中，常见的状态耦合约束主要有两类，文献[29]和文献[37]分别针对小天体软着陆和行星大气进入过程中，不规则引力场、气动加速度随状态的耦合约束，采用序列优化技术对着陆轨迹进行凸优化求解，使带有状态耦合约束的非凸问题得以转化为凸优化问题进行快速求解。但同时，采用多次迭代的序列优化技术也显著增大了运算量。

2.3 不确定环境下着陆轨迹优化研究现状

行星着陆过程中，着陆环境决定飞行器动力学行为和轨迹特性，主要包含大气环境、引力场环境、地形环境等。着陆环境存在建模误差、扰动等多种不确定因素，在轨迹优化过程中，研究和分析环境不确定性对着陆轨迹的影响，对提高着陆精度有着重要意义。

由于大气制动过程中存在显著的环境不确定性，因此抑制不确定性影响[19, 48-49]是轨迹优化的重要目标。Cui等[19]针对火星大气进入过程中存在的复杂扰动，提出一种基于线性协方差的大气进入轨迹优化方法，在传统的优化进入段末端高度的基础上，以减小进入过程中的环境扰动对开伞高度的影响为指标，并考虑了热流、过载等路径约束，采用GPOPS工具箱进行了相关的轨迹优化工作。Li等[49]提出了一种基于脱敏最优控制和直接配点法-非线性规划法的火星大气进入段轨迹规划方法，该方法考虑了气动参数不确定以及轨迹跟踪性能的影响。由于该方法规划的标称轨迹对进入过程中的扰动和不确定性不敏感，使得对于低升阻比探测器而言，相应的轨迹跟踪律设计难度大大降低。小天体动力制动着陆过程中存在极强的不确定性，探测器受到来自小天体引力摄动、太阳光压摄动、第三体引力摄动、不规则引力摄动等不同摄动源影响。针对小天体着陆过程中的不确定弱引力场对精确着陆的影响，Hu等[36]将脱敏最优控制的方法引入小天体着陆轨迹优化中，通过误差协方差分析构建脱敏最优性能指标，并采用Gauss伪谱法进行轨迹的优化求解。以上述工作为代表的轨迹优化研究成果，在基于传统确定性动力学系统的优化性能指标基础上，将不确定性的影响进行定量化并引入轨迹优化问题中，能够在不确定条件下，提高着陆轨迹精确性。由于不确定因素的影响指标(如灵敏度、线性协方差等)与确定性系统的性能指标(如末端高度、燃耗等)之间存在相互权衡的问题。当侧重考虑不确定性的影响时，将不可避免地导致最优轨迹的保守性增强，进而损失原有的确定性系统的指标最优性。同时，在研究中，不确定性影响因素的统计特性假设，对最终结果的有效性起着至关重要的影响。由于导航系统性能是影响参数不确定度的因素之一，导航系统可观测度与大气进入导航性能密切相关，以可观测度性能指标优化进入轨迹，是提高导航系统性能的重要手段[50]。

能控性和能达性分析方法是处理不确定环境中着陆轨迹优化的有效途径。能控性和能达性是反映着陆轨迹边界条件和动力学特性的两个重要方面[51-52]：在满足所有动力学约束和路径约束的条件下，反映能控性的能控集合是指给定末端状态约束的所有初始状态所构成的集合；反映能达性的能达集合是指给定初始状态约束的所有末端状态所构成的集合。通过能控集和能达集的求解，可直观反映满足边界条件的所有进入轨迹的空间分布，进而为初始状态/末端状态的选取提供依据。行星大气进入走廊就是能控集合的一个重要形式[53]。由于能控集与能达集的计算过程中涉及大量的轨迹计算，从而引出如下两个问题：1)由于着陆动力学的非线性，满足给定边界条件的着陆轨迹通常不止一条，这对分析能控/能达集中的轨迹特性及相关规律带来不便，通过采用选取相关性能指标进行轨迹优化可有效解决这一问题[48, 51]；2)大量轨迹计算使能控/能达集的求解过程异常耗时，而通过以能控/能达集边界作为性能指标进行优化求解，是获得能控/能达集的一种高效易行的方法[54]。因此，上述两个问题的存在使得轨迹优化方法称为能控/能达集计算中的重要手段。

图7 行星着陆能控集合[48]Fig.7 Controllable set for planetary landing[48]

3 着陆轨迹优化关键技术

3.1 非线性动力学的等价/近似变换技术

由于大气环境、引力场环境的特殊性，行星着陆动力学具有较强的非线性特征。依据行星着陆动力学特征，进行非线性动力学的等价/近似变换是进行轨迹优化的关键环节。在现有的局部逼近和全局逼近方法的基础上，进一步研究非线性动力学的变换技术，在逼近精度、解算效率、收敛条件等方面提升轨迹优化方法的综合性能。

3.2 复杂约束条件下的最优轨迹快速求解技术

行星着陆轨迹优化问题中，存在边界约束、路径约束和控制约束等复杂约束条件。这些约束条件对优化问题的可行域和收敛性具有显著影响，进而显著影响轨迹优化的解算效率。凸优化方法在收敛性、快速性等方面具有显著优势，但在复杂约束条件下获得普适等效凸化模型是制约其应用的技术瓶颈。

3.3 不确定条件下的能控/能达性分析技术

在行星着陆中存在多种不确定因素，对着陆动力学和着陆轨迹的显著扰动作用。因此，将确定性系统的能控/能达性分析方法引入不确定条件下的着陆轨迹问题分析，对于选择初始状态和着陆点，分析标称轨迹性能、揭示不确定条件下的运动行为具有重要的应用价值。

4 结束语

随着行星探测活动的不断深入，着陆轨迹规划的应用领域和优化目标也随之扩展：传统轨迹规划以飞行时间、燃料消耗、末端飞行高度等反映飞行品质的轨迹参数为性能指标。由于地外天体着陆过程中导航信息源严重受限，制导控制系统先验信息不确定性大，近年来，以导航系统可观测度、不确定参数灵敏度等为性能指标的轨迹优化方法逐渐受到重视，以应对地外天体着陆所特有的导航欠观测问题和动力学不确知环境。此外，以轨迹优化为基础的能控集/能达集计算方法在着陆初始状态、着陆目标点选择、不确定参数影响分析等任务设计层面发挥了重要作用。

凸优化方法由于在解算快速性与收敛性方面的优势，近年来在行星着陆轨迹优化领域受到广泛重视。但该方法对优化问题的数学形式有严格要求。因此，结合着陆动力学、约束条件的特点，寻求轨迹优化问题的普适等效凸化方法，是提高凸优化方法解算适应性的重要技术途径。