基于FPGA 的数字乘法器性能比较*

鞠 芳，马 昕，田 岚

(山东大学信息科学与工程学院，济南 250100)

在通信与信号处理系统中，乘法器是数字运算的重要单元，高性能乘法器是完成高性能实时数据运算和处理的关键。 随着 FPGA (Field Programmable Gate Array，现场可编程门阵列)技术的发展，FPGA 以其高度的灵活性和正在越来越多地替代ASIC和DSP 用于信号处理的运算［1］，然而常见的FPGA 芯片一般不具有现成的乘法运算单元，因而研究基于FPGA 的数字乘法器设计具有非常重要的意义。

针对FPGA 的乘法器设计，已有前人做了大量的工作，总结起来主要有阵列法［2］、查找表法、移位相加法［3］和Booth 法［4］，此外，还有以这几种方法为基础的改进方法，如有限域乘法器［5］等。实际应用中，有时需要乘法运算有较快的速度，有时则需要较少的硬件资源和适中的速度，乘法器的速度和面积优化对于整个CPU 的性能来说是非常重要的，因而有必要对乘法器的算法、结构及电路的具体实现做深入的分析并给出性能比较。本文针对查找表法、移位相加法和Booth 法等几种常用数字乘法器的设计方法在ALTERA 公司FPGA 系列进行了设计，并利用Quartus Ⅱ9.0 对这些设计进行了综合和仿真验证。最后从运算速度和所占用逻辑资源两方面对数字乘法器的性能进行了比较。

1 数字乘法器设计方法

乘法运算可以利用组合电路或时序电路来实现。组合电路乘法器比时序电路乘法器耗用硬件资源更多，但是运算速度更快。时序电路乘法器则需要几个时钟周期才能完成乘法运算，但是耗用的硬件资源较少。常见的组合电路乘法器有阵列乘法器和查找表乘法器，常见的时序电路乘法器有移位相加乘法器和Booth 乘法器，其它的乘法器多为以此为基础进行组合变形的，如有限域乘法器等。

设计组合电路乘法器需要根据乘法运算的原理由逻辑门实现，设计思路相对简单，而时序电路乘法器设计通常需有两个步骤:(1)选择数据通路结构(2)设计状态机以控制数据通路。对于给定的数据通路结构，状态机必须能生成适当的控制信号序列来控制数据的移动以产生乘积［6－8］。下面对阵列乘法器、查找乘法器、移位乘法器以及Booth 乘法器的设计方法作分析比较。

1.1 阵列乘法器

阵列乘法器是纯组合类型的乘法器，完全由逻辑门实现。乘数、被乘数和乘积都以并行方式提供［9］。

图1 给出了4×4 阵列乘法器的一种结构。该结构包括16个与门、8个全加器和4个半加器。在同步操作中，控制乘法器数据传输的时钟周期必须与电路中的最长路径相适应，该路径从乘数的最低位开始，途经加法器，到达乘积的最高位。加法器的进位路径和求和路径对最长路径都有影响，应将其延时均匀分布。

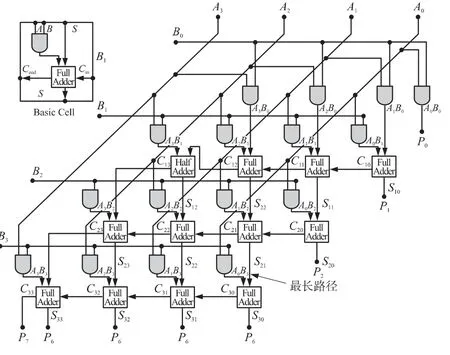
图1 阵列乘法器的一种结构

对于现在的FPGA 来讲，进位计算执行的速度要比和累加的速度快［10］，因此图2所示的结构对于FPGA 来讲效率更高。该结构的思想是:第一步将两个相邻的部分积相加，使部分积的数目减半。然后重复上述过程直到形成最终乘积。通过引入流水线技术，可以提高阵列乘法器的工作频率。

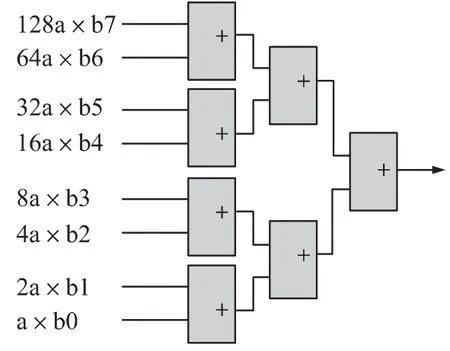
图2 FPGA 的快速阵列乘法器

1.2 查找表乘法器

查找表乘法器是将乘积直接存储在存储器中，将乘数和被乘数作为地址访问存储器，得到的输出数据就是乘法运算的结果。图3 给出了查找表乘法器的原理。查找表乘法器的速度只局限于所使用的存储器的存取速度，但是查找表的规模随着操作数位数的增加迅速增大。因此，查找表乘法器不适合位数较高的乘法。当乘数位数较高时可以将乘数分成几个部分，然后用低位数的查找表实现乘法运算。

图3 查找表乘法器原理图

1.3 移位相加乘法器

图4 给出了4×4 移位相加乘法器控制器的ASMD 图表:控制器初始状态为S_idle，复位完成后Ready 信号有效，表示时序乘法器空闲，可以接收数据。然后控制器等待外部输入Start 信号。Start 信号成立时，如果输入数据全0，则清空乘积寄存器并保持在状态S_idle，否则控制器应撤销Ready 信号，输出Load_words 信号并进入状态S_running。在状态S_running 判断计数器的值，如果计数器的值为操作数字节长度，控制器进入状态S_idle，乘法运算完成，否则判断乘积寄存器的最低位，如果乘积寄存器最低位为1，输出Add_shift 信号，如果乘积寄存器最低位为0 则输出Shift 信号。此间控制器运行在状态S_running，直到计数器的值等于操作数字节长度［10］。

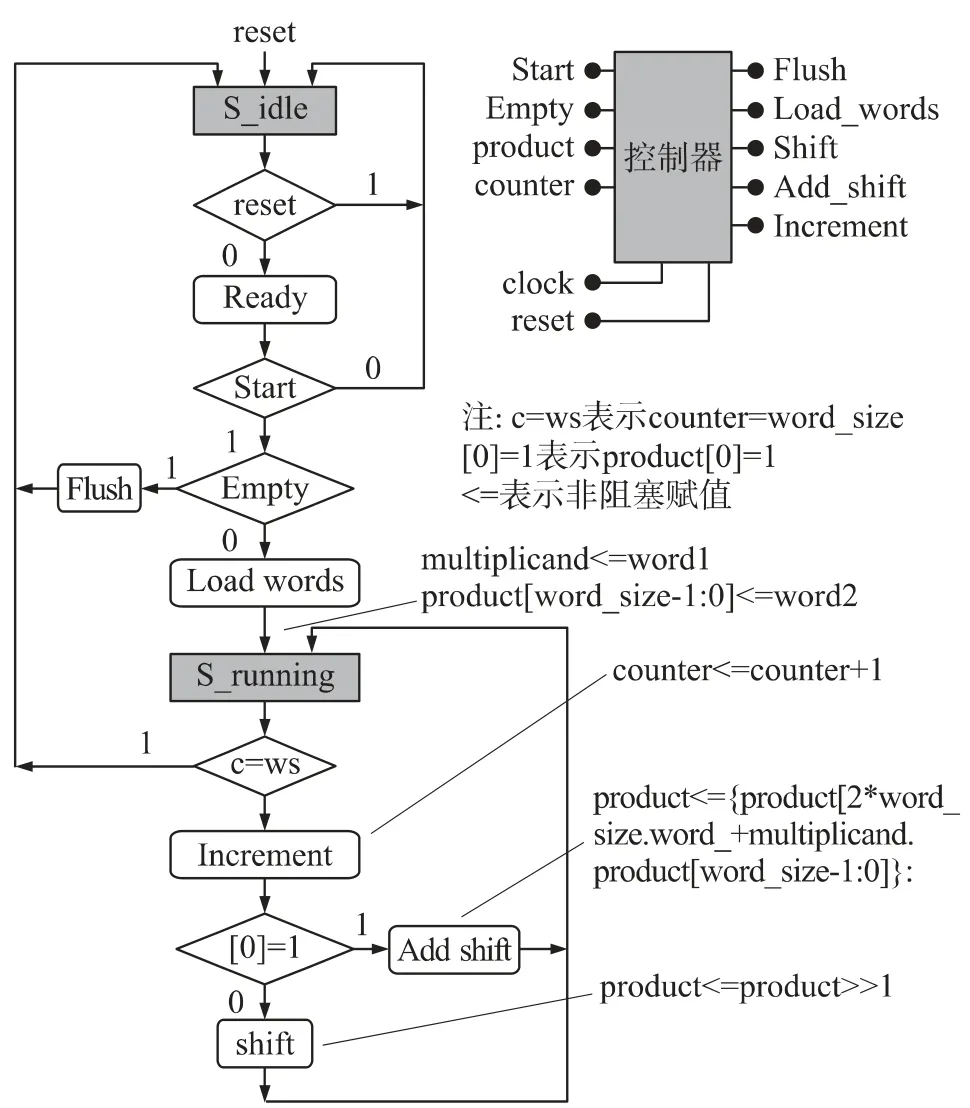
图4 移位相加乘法器的控制器方框图和ASMD 图表

图5 给出了4×4 移位相加乘法器的数据通路结构:该数据通路结构由存储被乘数的寄存器、一个加法器、一个存储乘数和乘积的移位寄存器组成。该结构把被乘数寄存器通过硬件连线与加法器相连，并作为乘积寄存器最左边的5 位。乘数的值最初存储在乘积寄存器最右边的4 位。所求得的部分积放在乘积寄存器的最左边，并将乘积寄存器的内容右移。在每一步中，由乘积寄存器的最低位决定是否将被乘数与乘积寄存器相加，直到乘数的所有位被移出乘积寄存器为止，最后留在乘积寄存器中的内容就是乘法运算的结果。

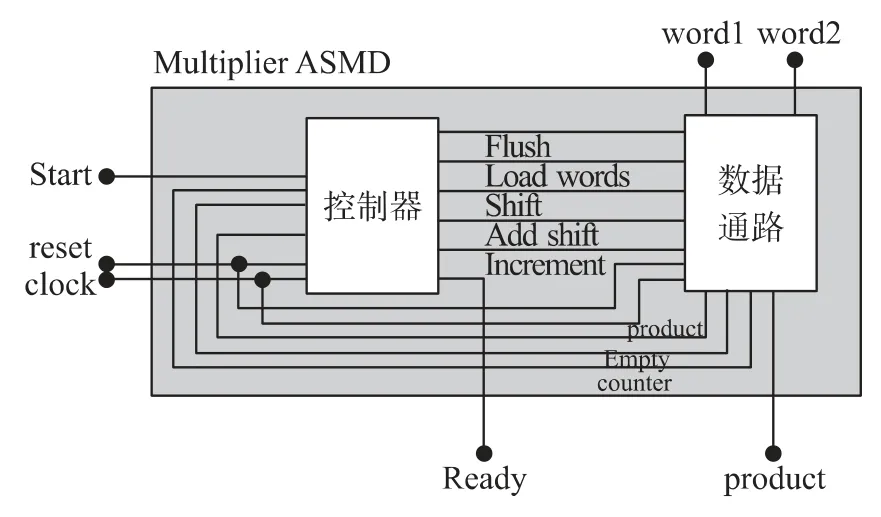
图5 移位相加乘法器的结构单元

移位相加乘法器的控制器产生的控制信号对数据通道的作用为:Flush 清空乘积寄存器Load_words控制数据通路将乘数和被乘数装入寄存器同时将计数器清零;Shift 控制乘积寄存器的移位;Add_shift控制被乘数和部分积的相加以及乘积寄存器的移位;Increment 控制计数器计数。

1.4 Booth 乘法器

使用Booth 算法的乘法器对乘数的位进行重新编码以减少完成乘法运算周期所需的加法运算次数。Booth 算法可以应用于以2 补形式表示的有符号数。因此使用Booth 重编码的硬件乘法器不需要修改就可以使用于负数运算［11－12］。

Booth 算法的关键在于它跳过了乘数中全1 的字符串，而将一系列加法运算用一次加法和一次减法来替代。例如，二进制数11110000 等于(28－1)－(24－1)=28－24=240。Booth 编码方案将检测乘数的全1 字符串，并用加减法运算得到的有符号数来取代它们，以对乘数重新进行编码。

表1 给出了Booth 重编码规则，该规则从最低位到最高位依次读取，两个相邻位(Mi，Mi－1)的值确定了Booth 重编码乘数的各个位BRCi，当算法读取两个相邻位时可形成BRCi，并用BRCi 来判断在跳到下一位之前是进行加法运算还是减法运算。该算法第一步放置一个0 到乘数最低位的右边，处理过程将遇到的第一个1 编码为1，跳过任何连续的1直到出现0，该0 可被编为1 以表示全1 字符串的结束，然后进行下一步的处理。

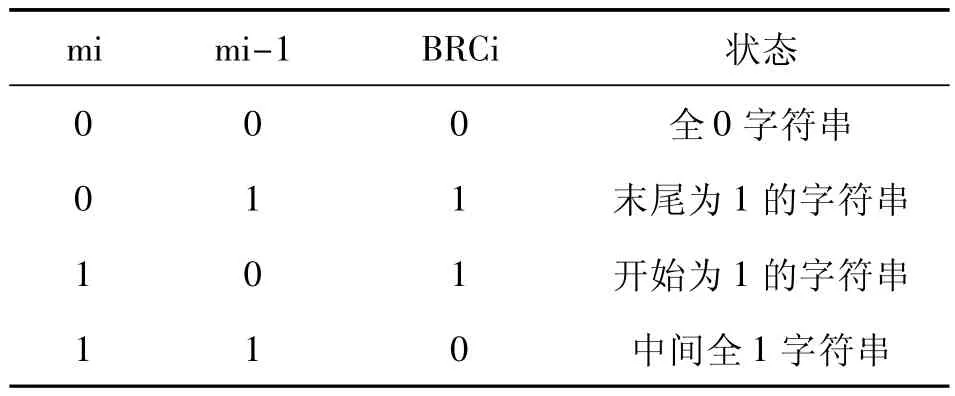
表1 补数的Booth 重编码规则

图6 给出了4×4 Booth 乘法器的状态转移图:控制器初始状态为S_idle，复位完成后Ready 信号有效，表示时序乘法器空闲，可以接收数据。然后控制器等待外部输入Start 信号。Start 信号成立时，控制器撤销Ready 信号，输出Load_words 信号并进入状态S_1。此后的状态转移取决于Booth 重编码BRCi，如果BRCi为1 则输出Add_shift 信号并进入下一状态，如果BRCi为2 则输出Sub_shift 信号并进入下一状态，如果BRCi为0或3 则输出Shift 信号并进入下一状态。直到进入状态S_5，此时控制器将输出Ready 信号并保持在状态S_5，直到外部输入Start 信号控制器才进入状态S_1 并输出Load_words 信号重新装载乘数和被乘数，开始新一次的乘法运算。图7 给出了4×4 Booth 乘法器的数据通路结构:该数据通路结构由存储被乘数和乘数的两个移位寄存器、一个加法器和一个存储乘积的寄存器组成。

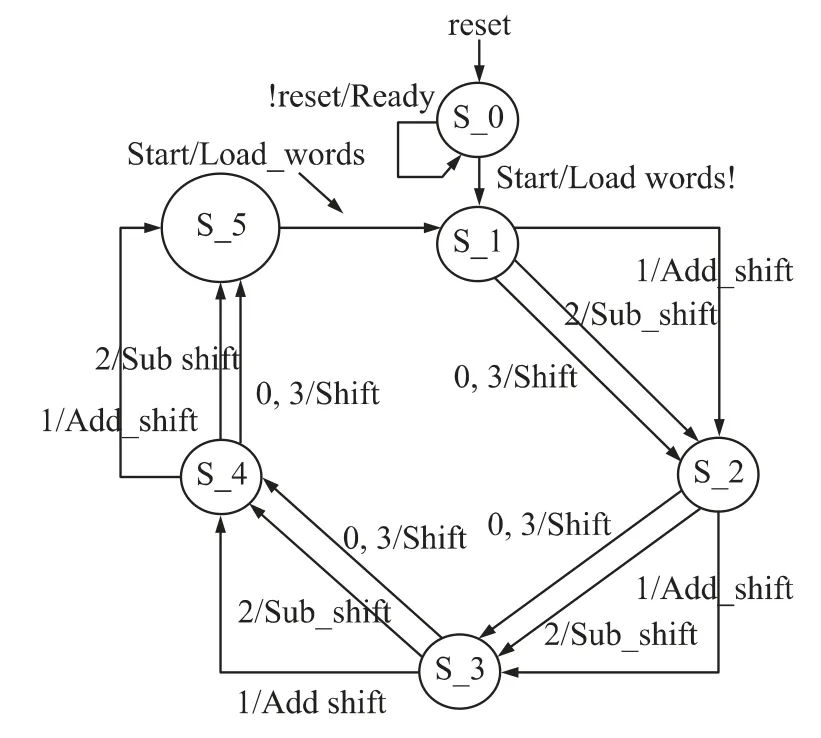
图6 Booth 时序乘法器的STG

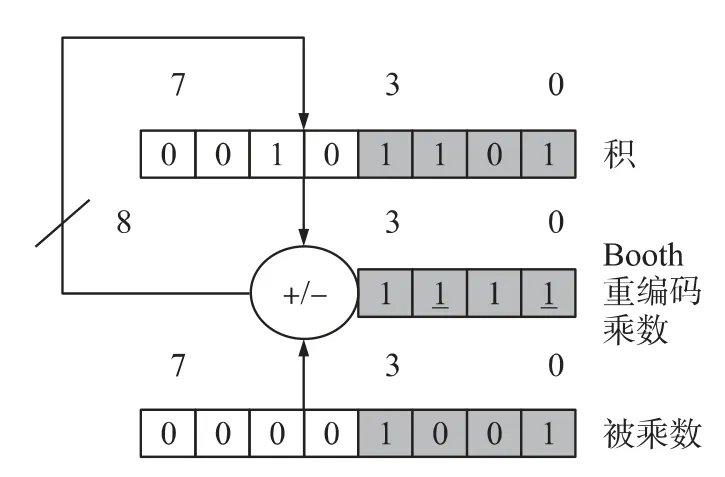
图7 Booth 乘法器的数据通路结构

4×4 Booth 乘法器的控制器产生的控制信号对数据通道的作用为:Load_words 控制数据通路将乘数和被乘数装入寄存器;Shift 控制乘数寄存器和被乘数寄存器的移位;Add_shift 控制部分积和被乘数的相加以及乘数寄存器和被乘数寄存器的移位;Sub_shift 控制部分积和被乘数的相减以及乘数寄存器和被乘数寄存器的移位。

2 各种数字乘法器设计方法的性能比较

根据上述原理分别设计了4×4 数字乘法器和16×16 数字乘法器，利用Quartus Ⅱ9.0 对各种数字乘法器进行编译、综合及功能仿真(目标芯片为cyclone Ⅱ系列中的EP2C8Q208C8)。4×4 位数字乘法器的综合结果见表2。16×16 位数字乘法器的仿真结果见表3。

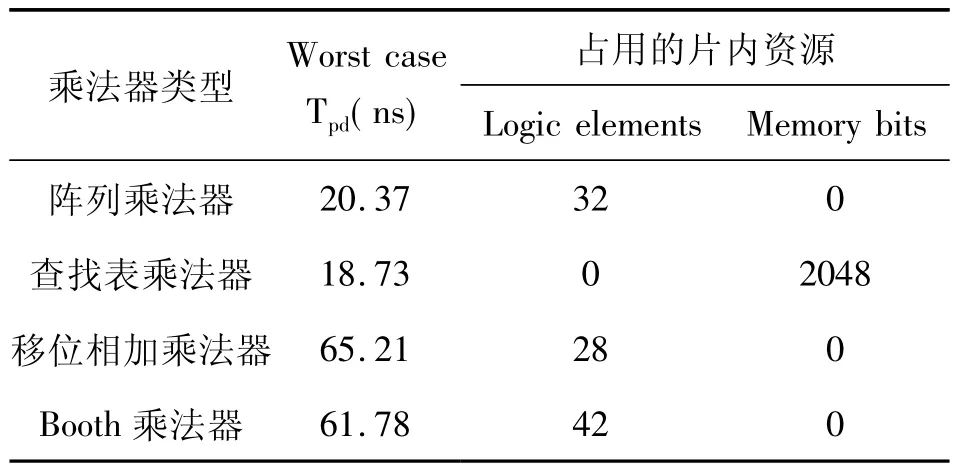
表2 4×4 位乘法器的综合结果

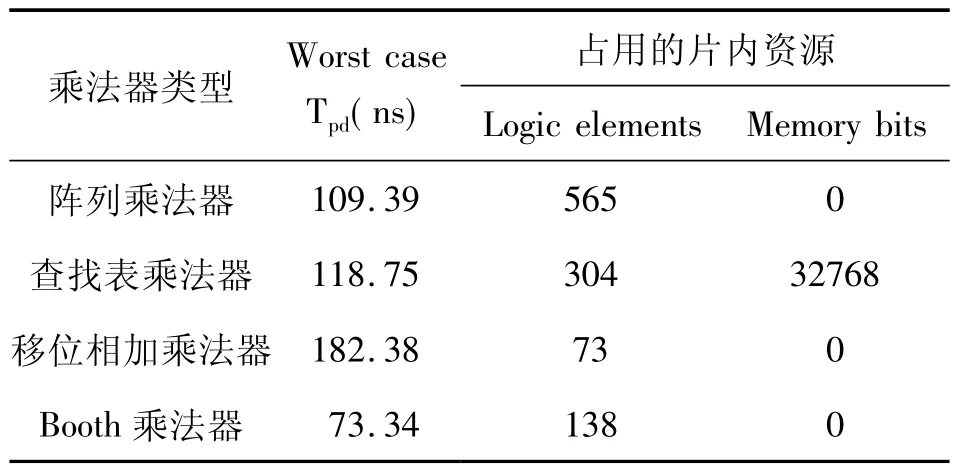
表3 16×16 位乘法器的综合结果

由以上综合及仿真结果可知:对于4×4 位乘法器，阵列乘法器通过增加硬件资源耗用提高了运算速度。查找表乘法器运算速度高于阵列乘法器，其硬件资源耗用也高。移位相加乘法器完成一次乘法需要5个时钟周期，运算时间较长，但其硬件资源的耗用最少。Booth 乘法器速度上与移位相加乘法器差不多，但资源消耗较大，由此可见对于位宽较小时Booth 乘法器结构的性能没有优势。

对于16×16 位乘法器，阵列乘法器通过增加硬件资源耗用并适当的使用流水线技术提高了运算速度，而查找表乘法器通过使用存储单元存储乘法结果达到运算速度的提高，但是其速度已明显低于阵列乘法器，只是其逻辑单元资源的消耗比阵列乘法器少，但却要占用较多的片内存储器资源。移位相加乘法器完成一次乘法需要17个时钟周期，运算时间比其他三种乘法器的都长，但硬件资源的耗用最少。Booth 乘法器速度最快，而同时资源消耗仅高于移位相加乘法器，综合优势明显，由此可见对于位宽较大时，Booth 乘法器体现出了明显的性能优势。

组合乘法器的硬件资源耗用随着乘法器字节长度增加而大幅度增长，而时序乘法器的硬件资源耗用随字节长度增加增长速度较缓，除Booth 乘法器之外，其他三种乘法器同时完成乘法运算所需的时钟周期将随字节长度呈明显增长趋势。

3 结束语

本文应用Verilog 语言，设计了四种数字乘法器，并对它们的性能进行了比较。从仿真和综合的结果看，随着位宽的变化，方法的相对效果会发生改变。对于具有较宽数据位的乘法器来说，使用Booth乘法器有明显的优势。而位宽较小时，阵列乘法器的综合优势明显。如果仅考虑资源占用，移位相加乘法器是较好的选择。在实际应用中应根据系统的要求选择合适的乘法器设计方法。数字乘法器的结构多种多样，本文仅针对四种常见乘法器做了分析和比较，实际应用时可根据实际情况选择合适的乘法器设计方法。

［1］马秀娟，牛进鹏，考丽，等.高速数据采集系统中的FPGA 的设计［J］.电子器件，2007，30(4):1372－1379.

［2］Habibi A，Wintz P A.Fast Multipliers［J］.IEEE Transactions on Computers，1970，C－19(2):153－157.

［3］王江，黄秀荪，陈刚，等.一种RISC 微处理器的快速乘除法运算设计与实现［J］.电子器件，2007，30(1):162－166.

［4］汤晓慧，杨军，吴艳，等辉.基于Booth 算法的32×32 乘法器IP核设计［J］.电子器件，2005，28(1):218－220.

［5］鲍可进，郑博.基于FPGA 的有限域乘法算法的分析和比较［J］.计算机工程，2008，34(23)247－248.

［6］Donald E Thomas，Philip R Moorby 著.刘明业，蒋敬旗，刁岚松等译.硬 件 描 述 语 言Verilog［M］.北 京:清 华 大 学 出 版社，2001.

［7］Uwe Meyer-Baese 著.刘凌译.数字信号处理的FPGA 实现［M］.北京:清华大学出版社，2006.

［8］Michael D Ciletti 著.张雅绮，李锵， 等译.Verilog HDL 高级数字设计［M］.北京:电子工业出版社，2005.

［9］Amberg P.Pinckney Harris，Parallel N.High-Radix Montgomery Multipliers［C］//proceedings of 42nd Asilomar Conference on Signals，Systems and Computers.Pacific Grove，CA，Oct.26－29，2008:772－776.

［10］Gnanasekaran R.A Fast Serial-Parallel Binary Multiplier［J］.IEEE Transactions on Computers，1985，34(8):741－744.

［11］Booth A D.A Signed Binary Multiplication Technique［J］.Quarterly Journal of Mechanics and Applied Mathematics，1951，4(2):236－240.

［12］Wallace C S.A Suggestion for a Fast Multiplier［J］.IEEE Transactions on Electronic Computers，1964，13(2):14－17.