基于FPGA的流水线单精度浮点数乘法器设计*
彭章国,张征宇,2,王学渊,赖瀚轩,茆 骥
(1. 西南科技大学 信息工程学院,四川 绵阳 621010;2. 中国空气动力研究与发展中心,四川 绵阳 621000)
基于FPGA的流水线单精度浮点数乘法器设计*
彭章国1,张征宇1,2,王学渊1,赖瀚轩1,茆 骥1
(1. 西南科技大学 信息工程学院,四川 绵阳 621010;2. 中国空气动力研究与发展中心,四川 绵阳 621000)
针对现有的采用Booth算法与华莱士(Wallace)树结构设计的浮点乘法器运算速度慢、布局布线复杂等问题,设计了基于FPGA的流水线精度浮点数乘法器。该乘法器采用规则的Vedic算法结构,解决了布局布线复杂的问题;使用超前进位加法器(Carry Look-ahead Adder,CLA)将部分积并行相加,以减少路径延迟;并通过优化的4级流水线结构处理,在Xilinx®ISE 14.7软件开发平台上通过了编译、综合及仿真验证。结果证明,在相同的硬件条件下,本文所设计的浮点乘法器与基4-Booth算法浮点乘法器消耗时钟数的比值约为两者消耗硬件资源比值的1.56倍。
浮点乘法器;超前进位加法器;华莱士树;流水线结构;Vedic算法;Booth算法
0 引言
阵列乘法器是采用移位与求和的算法而设计的一种乘法器[1]。阵列乘法器具有规则的结构,易于布局布线等特点。随着乘数位宽的增加,部分乘积的个数也成倍地增加,部分乘积项数目决定了求和运算的次数,直接影响乘法器的速度。修正的Booth算法对乘数重新编码,可以减少相加的部分乘积的数量,因为部分积的存在,部分积相加过程与阵列乘法器没有太大差异。为了实现速度的提高,Wallace树结构可以改变部分积求和方式,将求和级数从O(N)减少到O(logN)。因此现有很多乘法器设计都采用修正的Booth算法与Wallace树结构相结合的方法。但是Wallace树结构缺乏规整性,布局布线困难;引线的延长导致寄生电容增加,妨碍了电路速度的进一步提高。同时不规则的结构会增加硅板的面积,并且由于路由复杂而导致中间连接过程的增多,继而导致功耗的增大[2-3]。
吠陀乘法器具有其独特规则的结构,随着乘数位宽的增加,门延迟和面积的增加很缓慢,因此乘法器能够在时间延迟、面积、功耗上达到最优。文献[4]设计了一种高速的4×4位吠陀乘法器,通过实验证明了4×4位吠陀乘法器比同位宽的阵列乘法器、Booth算法乘法器的运算速度快;文献[5]设计了单精度的浮点乘法器,其中尾数计算部分分别采用了吠陀乘法器和Booth算法乘法器两种方法,结果证明吠陀乘法器在时间延迟和面积上都优于Booth算法乘法器;文献[6]在吠陀乘法器中分别采用行波进位加法器(eRipple Carry Adders,RCA)和超前进位加法器(eCarry Look-ahead Adder,CLA)计算部分乘积的和,通过实验数据对比,采用超前进位加法器可以获得更高的速度和占更少的面积。然而对于海量的图像数据进行浮点数乘法运算时,每一组数据从运算开始到结束期间会产生时间延迟,可以在乘法器中加入流水线结构来减少延迟时间,为此本文设计了一种基于吠陀数学的流水线浮点乘法器。
1 总体设计
本文所设计的单精度浮点数乘法器主要包含以下几个部分:24位吠陀乘法器、一个8位无符号加法器、一个9位无符号减法器、一个符号位计算单元和一个标准化单元。其结构框图如图1所示。

图1 单精度浮点数乘法器结构图
1.1 符号位与阶码计算
IEEE 754标准[7]为二进制浮点运算提供了一个精确的浮点数格式计算规范操作及异常处理。这一标准定义了32位单精度浮点数和64位双精度浮点数两种类型。它们都分别由符号位、尾数、阶码组成,表1给出了单精度浮点数格式,由式(1)表示为:
P=(-1)S2(Exp-Bias)M
第三,高校要利用“互联网+监管”的方式来营造良好的网络环境。“互联网+”时代的到来拓展了大学生企业家精神教育的新内容,形成了开放、互通、共享的教学模式,同时还实现了从大一统教学到个性化教学的转变,大学生实现了从被动学习到主动学习的转变。但是庞大冗杂的信息、开放自由的环境也给正处于成长期的大学生提供了负面信息传播和宣泄的场所,高校要实时对互联网中良莠不齐的信息进行筛选与甄别,及时关注学生的思想形态,营造风清气正、积极向上的网络环境。
(1)
式中S代表符号位;Exp表示阶码;Bias为固定值,其值为127;M为尾数。

表1 单精度浮点数的格式
(1)符号位计算:两个数相乘的结果的符号位由这两个乘数的符号位相异或(⊕)得到,如式(2)所示。
S=S1⊕S2
(2)
式中S1、S2为两个单精度度浮点数的符号位,S为两者之间的异或结果。
(2)阶码计算:该加法器模块主要将两个乘数的阶码相加,其结果再减去偏差值而得到相乘后结果的阶码,如式(3)所示。
PExp=AExp+BExp-Bias
(3)
式中AExp、BExp为两个单精度浮点数的阶码;Bias为固定值,其值为127。
1.2 24位吠陀乘法器的逻辑电路设计

图2 2×2吠陀乘法器
吠陀乘法器是基于吠陀数学而设计的。吠陀数学是Sri Bharati Krishna Tirthaji(巴拉蒂·克里希纳·第勒塔季)在研究印度古代吠陀经文的基础上重构的数学计算体系,其中包括了算术、代数、几何、三角函数和微积分等学科的处理方法。本文设计的24位吠陀乘法器是基于Urdhva Tiryakbhyam Sutra(字面意思是垂直和横向)而设计的,2位吠陀乘法器的结构框图如图2所示,它由4个与门和2个半加器组成,它是24位吠陀乘法器的基本组成单元。
根据2位吠陀乘法器的结构,一个4位吠陀乘法器可以分解为4个2位吠陀乘法器和3个4位加法器,如图3所示。
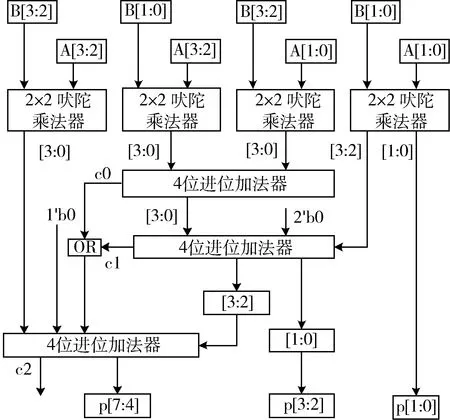
图3 4×4位吠陀乘法器
同理,一个8位吠陀乘法器可以由4个4位吠陀乘法器和3个8位加法器组成,因此,n位的吠陀乘法器能够使用4个n/2位吠陀乘法器和3个n位的加法器实现。综上,n位的吠陀乘法器被分解成n/2个n/2位的乘法器,然后这些较小位宽的乘法器(n/2位)再次分为更小位宽的乘法器(n/4位),直到被乘数位宽为2位,从而简化整个增殖过程。
由吠陀乘法器的结构可知,乘法器中会用到进位加法器将各部分积并行相加,随着加法器的引入,必然会产生路径时间延迟,从而降低乘法器的运算速度。本文使用CLA先行求得多位加法各位间的进位值,它由进位位产生进位,各进位彼此独立,不依赖于进位传播,从而减少等待进位所需要的时间延迟。其推导过程如下:
设二进制加法器的第i位为Ai和Bi,输出为Si,进位输入为Ci,进位输出为Ci+1,则有:
Si=Ai+Bi+Ci
(4)
Ci+1=Ai&Bi+Ci&(Ai+Bi)
(5)
令:Gi=Ai&Bi,Pi=Ai+Bi,则有:
Ci+1=Gi+Ci&Pi
(6)
只要Gi=1 ,就会产生向Ci+1位的进位,称Gi为进位产生函数。同样,只要Pi=1,就会把Ci传递到Ci+1位;其中Pi为进位传递函数。随着位数的增加式(5)会加长,但总保持三个逻辑级的深度,因此形成进位的延迟是与位数无关的常数。
24位吠陀乘法器结构图如图4所示,其中包括1个16位吠陀乘法器、2个16×8位吠陀乘法器、1个8位吠陀乘法器、3个CLA。

图4 24位吠陀乘法器结构图
1.3 流水线结构设计
为了提高FPM对批量数据的运算速度,根据乘法器内部独特的结构,乘法器中采用了4级流水线进行处理,如图5所示。通过对24位吠陀乘法器的结构进行分析可知,该乘法器主要由4个不同位宽的吠陀乘法器级联而成,因此从最基本的2位吠陀乘法器单元出发,在每一个乘法器单元中加入了移位寄存器,形成流水线结构。
2 实验结果与分析
整个FPM设计使用Verilog HDL语言描述,然后在Xilinx®ISE14.7集成软件环境下进行了编译、综合及功能仿真,最后在XiLinx公司的Virtex-6(xc6vlx240t-1ff1156 )硬件实验平台上进行了验证。FPM中尾数乘积部分是其最重要的部分,因此设计了采用Vedic、基2-Booth、基4-Booth三种算法的24位无符号整数乘法器,并对三种算法的乘法器消耗的硬件资源进行了对比,如表2所示。
由表2可知,由于乘法器中每一级都包含了3个CLA,Vedic算法乘法器消耗的LUTs数目是三种算法乘法器中最多的,而在其他方面的资源消耗是最少的。基4-Booth算法乘法器相对于基2-Booth算法乘法器消耗了更多的资源。三种算法的24位无符号整数乘法器的仿真波形如图6~图8所示。其中基2-Booth算法完成一次计算需要52个时钟周期,基4-Booth算法需要15个时钟周期,而Vedic算法乘法器由组合逻辑电路设计而成,不需要消耗时钟周期。
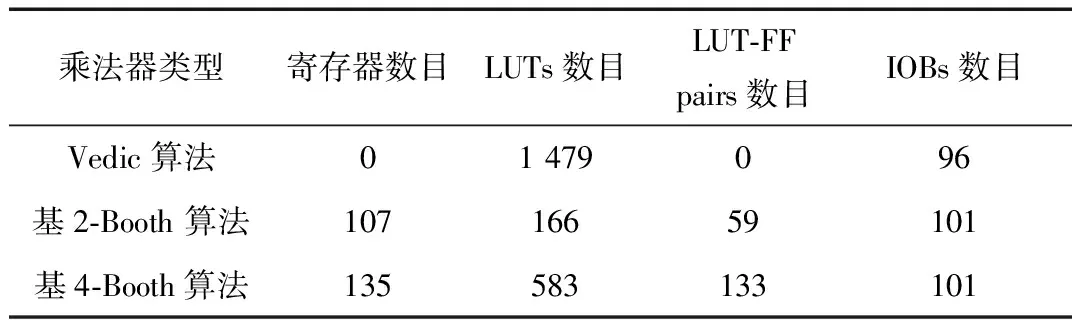
表2 三种算法的24位无符号整数乘法器消耗硬件资源数目对比 (个)

图6 基2-Booth算法的24位无符号整数乘法器仿真图

图7 基4-Booth算法的24位无符号整数乘法器仿真图

图9 基2-Booth算法的浮点乘法器仿真图

图10 基4-Booth算法的浮点乘法器乘法器仿真图

图8 Vedic算法的24位无符号整数乘法器仿真图

图11 Vedic算法的浮点乘法器乘法器仿真图
表3列出了基2-Booth、基4-Booth两种算法设计的FPM与本文设计的基于吠陀数学的流水线FPM在消耗FPGA资源数目上的对比。
由表3所知,三种方法的FPM在资源、时钟周期消耗上与无符号整数乘法器所得结论基本一致。其中基2-Booth算法FPM完成一次计算需要52个时钟周期,基4-Booth算法需要24个时钟周期,Vedic算法的浮点乘法器需要9个时钟周期。综上,Vedic算法FPM在运算速度上更快,这是因为吠陀乘法器的部分积并行相加的结果,采用高速的超前进位加法器,使得运算速度进一步提升。三种算法的浮点数乘法器的仿真波形如图9~图11所示。
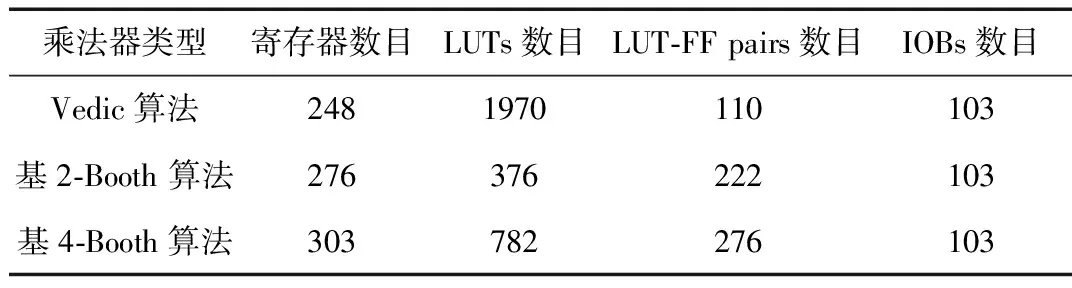
表3 三种算法的浮点数乘法器消耗硬件资源数目对比 (个)
通过计算基4-Booth FPM与本文设计的FPM消耗资源、时钟周期数目的比值发现,本文设计的FPM与基4-Booth算法FPM消耗时钟数的比值约为两者消耗FPGA资源比值的1.56倍。
3 结论
本文设计了一种基于吠陀数学的流水线FPM。乘法器采用Vedic算法,并在其结构中采用超前进位保留加法器将产生的部分积结果并行相加,从而减少了电路延迟,4级流水线结构也使得乘法器运算速度进一步得到了提高。相比于华莱士树算法相结合设计的乘法器,吠陀乘法器具有较规则的结构,容易布局布线。虽然本文设计的浮点乘法器消耗了更多的资源,但是在速度上获得了提高。
[1] 胡正伟,仲顺安. 一种多功能阵列乘法器的设计方法[J]. 计算机工程, 2007, 33(22): 23-25.
[2] 夏炜, 肖鹏. 一种高效双精度浮点乘法器[J]. 计算机测量与控制,2013, 21(4): 1017-1020.
[3] 李飞雄, 蒋林.一种结构新颖的流水线 Booth 乘法器设计[J]. 电子科技, 2013, 26(8):46-48.
[4] KARTHIK S, UDAYABHAUN P. FPGA implementation of high speed vedic multipliers[C].International Journal of Engineering Research and Technology. ESRSA Publications, 2012, 1(10).
[5] KONERU P, SREENIVASU T, RAMESH A P. Asynchronous single precision floating point multiplier using verilog HDL[J]. IJ of Advanced Research in Electronics and Communication Engineering, 2013.
[6] ANJANA S, PRADEEP C, SAMUEL P. Synthesize of high speed floating-point multipliers based on Vedic mathematics[J]. Procedia Computer Science, 2015, 46: 1294-1302.
[7] IEEE 754-2008, IEEE Standard for Floating-Point Arithmetic[S]. 2008.
彭章国 (1990-),男,硕士研究生,主要研究方向:数字信号和视频图像处理技术。
张征宇 (1971-),通信作者,男,博士,研究员,主要研究方向:光学测量及其在风洞实验中的应用等。E-mail:zzyxjd@163.com。
王学渊 (1974-),男,博士,副教授,主要研究方向:测试数据采集与处理。
A single precision floating-point multiplier design of assembly line based on FPGA
Peng Zhangguo1,Zhang Zhengyu1,2,Wang Xueyuan1,Lai Hanxuan1,Mao Ji1
(1.School of Informatin Engineering, Southwest University of Science and Technology, Mianyang 621010,China;2. China Aerodynamics Research and Development Center, Mianyang 621000,China)
Considering the existing floating-point multiplier based on Booth algorithm and Wallace tree, which has slow speed and complex layout, a single precision floating-point multiplier is designed using Vedic mathematics. The Vedic multiplier(VM) has a regular structure therefore can be easily placed and routd in a silicon chip. Carry look-ahead adder (CLA) structure is used to add the part of the product in parallel for reducing the path delay. The floating-point multiplier design employs an optimized 4-stage pipeline processing and the simulation and synthesis are done in Xilinx®ISE 14.7.The results prove that under the condition of the same hardware, the ratio of consumed clock number between the designed multiplier in this paper and arithmetic point multiplier based on 4-Booth is about 1.56 times than that of consumed hardware resources.
floating-point multiplier; carry look-ahead adder; Wallace tree; pipeline structure; Vedic algorithm; Booth algorithm
国家自然科学基金(51475453);国家自然科学基金(11472297)
TP331.2
A
10.19358/j.issn.1674- 7720.2017.04.022
彭章国,张征宇,王学渊,等.基于FPGA的流水线单精度浮点数乘法器设计[J].微型机与应用,2017,36(4):74-77,83.
2016-08-29)

