一种混合结构的新型近似加法器
王保坤,班 恬
(南京理工大学电子工程与光电技术学院,江苏南京210094)
随着超大规模集成电路技术的飞速发展,电路中各种错误的发生是不可避免的。利用容错技术可以提高电路的可靠性[1]。近年来,集成电路(Integrated Circuits,IC)设计中由芯片功耗增大所带来的挑战引起了人们的广泛关注[2]。一些具有容错能力的应用工程(如多媒体处理、模式识别与机器学习等)在计算过程中可容纳一些错误。对于这些与人类听觉或视觉等感官有密切关系的应用场合,一些错误可以忽略不计。这就为通过降低精度要求而实现节能设计提供了良好的机会。
先前的文献已经提出了不同种类的近似加法器结构。文献[3]提出了低位或门加法器(Lower-Part-OR Adder,LOA),它利用精确加法器来计算较高位的和,利用逻辑或门来计算较低位和的近似值。除此之外,不精确部分的最高两位通过逻辑与门产生进位输入信号并传递给精确部分以提高整个近似加法器的运算精度。相对于经典精确加法器,LOA拥有更少的面积开销与功率损耗,但其错误率却极高。文献[4]提出了容错加法器(Error-Tolerant Adder I,ETAI)。这种加法器利用修改后的逻辑异或门来计算较低位的近似和,用精确加法器计算较高位的精确和。通过实验测试,该近似加法器对于较小输入运算的错误率较高。为解决这一缺陷,该文献作者在文献[5]中提出了ETAII。利用分块的思想,将整个电路结构分成若干个子加法器模块,这样可以将整条进位传输路径截断成较短路径,因而减少电路的延时与动态功耗。为进一步提高ETAII的正确率,文献[5]提出了ETAM。与ETAII仅考虑前一个模块的进位信号不同,ETAM里的多个进位产生模块级联为较高位的模块提供进位输入信号。文献[6]提出了精度可配置加法器(Accuracy-Configurable Approximate Adder,ACA adder)。该近似加法器可以运行在精确模式与近似模式之下。它利用若干个子加法器来计算和的部分值,运算精度较高。但由于电路配置了错误检测与纠正模块,导致较大的功耗与面积。文献[7]提出的预测进位选择加法器(Speculative Carry Select Addition,SCSA)的思想来自于对加法运算进位链的推断。每个子模块的进位输出信号仅由该模块所有位来决定,通过数据选择器来选择不同情况下进位输出信号的数值,这将导致更大的面积与功耗。文献[8]提出了一种非常有效的进位推断方法,该方法可保证近似加法器有较低的相对误差,同时有较少的面积与功耗。
本文提出了一种具有混合结构的新型近似加法器(HYB adder),该加法器可以在计算精度与其他性能参数之间获取平衡。因为最高有效位在计算中起到了更为重要的作用,因此该加法器从最低位到最高位分别由3种不同精度、不同结构的子模块组成。
1 混合结构近似加法器(HYB adder)
1.1 近似加法器的结构
以16位加法器为例。将16位加数分成精确部分(高8位)与非精确部分(低8位)。精确部分由经典精确加法器组成,如行波进位加法器(Ripple Carry Adder,RCA)或超前进位加法器(Carry Lookahead Adder,CLA)。非精确部分被分成两个子模块,其具体结构如下说明:
1)低位部分:为截断最低4位加数的进位传递路径,此部分没有进位产生。图1为1位精确加法器与1位近似加法器的卡诺图(二者均不考虑进位输入信号)。近似加法器将和“10”转化为“01”,因而此部分可采用逻辑或门来参与计算。这样做可有效减少电路面积与延时。
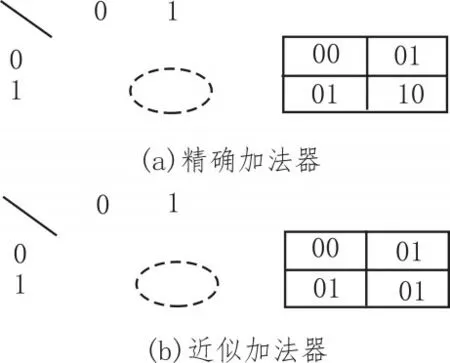
图1 精确1位加法器与近似1位加法器不考虑进位输入时的卡诺图
2)中间部分:采用一种省略最低位进位的近似超前进位加法器来计算中间4位加数的和。设加法器第i位的两个输入分别为ai、bi,进位输入为ci。第i位的进位传递信号pi与进位产生信号gi的表达式如下所示:

第i位的近似进位输出与近似和由下式表示:
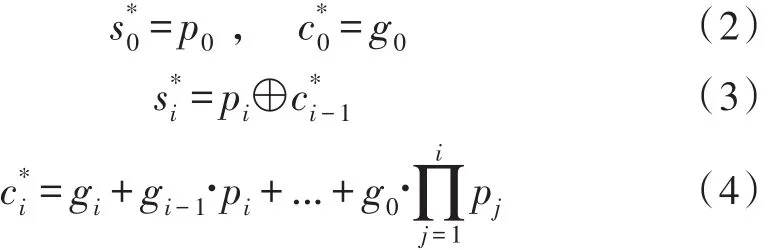
其中,i>1。
如果pi=1,ci=ci-1,代表第i-1位的进位输出信号传递到了第i位来。如果gi=1,ci=1,代表了第i位产生了进位输出。该部分还将为高位精确部分产生一个进位输入信号,以增加运算的精确度。下图是16位HYB Adder的电路结构图:

图2 16位HYB Adder的电路结构图
1.2 近似加法器的误差特性分析
1)错误率:将N位近似加法器分成三部分,其中包括m个较高位、p个中间位和l个较低位,即N=m+p+l。
最低部分的误差分析:当此部分任一位的两个输入同时为1时,即产生了进位输出信号,此时输出结果错误。因此,此部分产生错误结果的概率为:

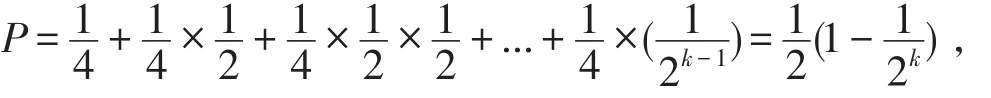
因此,近似超前进位加法器的错误率为:


表1列出了l与p取不同值时该近似加法器的错误率(k=4)。

表1 l与p取不同值时的错误率
2)误差距离:相对于错误率,误差距离(Error Distance,ED)与平均误差距离(Mean Error Distance,MED)可更有效地衡量近似电路的运算性能[9]。对于近似加法器来说,ED是指精确的和(S)与近似的和(S’)之差的绝对值,即

其中,S是精确加法器的和,S’是近似加法器的和。
MED指对给定输入向量下ED的平均值[9],是评估多位加法器运算性能的有效指标。

其中,P(EDi)是EDi的概率,qi是加法器中第i位的错误率。
为计算MED,本文利用Verilog HDL语言搭建了一个有效平台,其结构如图3所示:

图3 计算MED的平台结构图
此平台工作在clk的上升沿,由异步复位信号rst进行初始化。其中,信号x代表精确加法器(Accurate Adder)模块与近似加法器(Approximate Adder)模块的输入数据,其范围是0~2N-1。比较模块(Comparator)用以比较两个加法器产生的输出(ya与yap)。比较模块中的计数器(count)用来计算在给定相同输入下两个加法器产生不同输出的个数。由于遍历所有输入的组合,qi的值便可由count与2N之比得到。
2 比较与分析
本文将所提出的近似加法器用Verilog HDL语言描绘,并利用28纳米的FD-SOI标准单元库[10]在Cadence RTL Compiler下进行了电路综合。图4给出了16位HYB Adder的电路结构图,其各个部分的位宽为m=8,l=p=4。

图4 16位近似加法器综合后的结构图
图4中最下方的模块为HYB Adder中的低位部分,即逻辑或门组成的模块。中间位置为HYB Adder的中间部分结构,即近似CLA。最上方则为高位部分,是精确加法器RCA模块。
为了比较HYB Adder与其他加法器在面积、延时、功耗与误差性能方面的表现,本文也对经典精确加法器RCA以及其他4个已被提出的近似加法器进行了电路综合,各加法器的子模块位宽都选择了4位(k=4),精确部分都使用了相同的RCA电路结构。LOA、ETA-I与HYB加法器的精确部分与不精确部分均为8位位宽。为保证电路可比性,我们没有将ACA的错误检测与纠正电路考虑进来,因为这样会增加电路额外的面积开销与延时。实验结果如下表所示。

表2 各16位加法器性能参数比较
由于完全利用逻辑或门进行低位运算,LOA拥有比HYB更小的面积与功耗,但HYB中间部分更为精确的运算机制使其比LOA的错误率更低。因为截断了整个或部分的进位传播路径,所以ETA-I比HYB的延时与功耗更小。然而由于配置了修改后的异或门与控制信号产生单元,ETA-I的面积开销比HYB更大。同时,ETA-I高达接近90%的错误率可能会限制其在实际工程中的运用。ACA在延时方面优势最突出,因为其缩短的进位链减少了关键路径延时。SCSA运行速度较快且错误率较低,但由于进位选择机制使其配置了包含两个经典精确加法器的窗口加法器,因此SCSA的面积开销与功耗在所有加法器中最大。尽管HYB比ACA与SCSA的错误率要高出不少,但ACA与SCSA的高位运算精度却不乐观,这些都在其平均误差距离上有所体现。在参与比较的所有加法器中,HYB的平均误差距离最小,因此HYB在运算电路的应用是有很大意义的。
3 近似加法器在DCT/IDCT中的应用
DCT/IDCT的图像处理程序中包含了大量的加法、乘法与除法运算[11-13],我们将此程序中的所有32位的精确加法器替换成了32位的近似加法器(l=8,p=8,m=16)。
通常用峰值信噪比(Peak to Signal Noise Ratio,PSNR)来衡量图像的失真程度[14-15],其公式如(10)所示。PSNR的值越大,代表处理过的图像失真越小。

其中,MAX代表图像像素值的最大值,MSE为原始图像I与经过DCT/IDCT重构后的图像K(二者灰度图的像素矩阵均为m×n)的均方误差[16-17],其定义如下:

表3是利用近似加法器重构后图像的PSNR值,图5是重构后的图像。

表3 精确加法器与近似加法器PSNR值(dB)的比较

图5 精确加法器与近似加法器重构后的图像
从表3可以看出,由近似加法器重构后图像的PSNR值仅仅比精确加法器重构后图像的PSNR值损失了一点,而这一点损失也可完全被人眼忽略。
4 结束语
本文基于近似的思想,提出了一种新型混合结构的近似加法器HYB Adder。在故意牺牲一定精度的前提下,使加法器在延时、面积与功耗等性能参数方面有较大提升。本文搭建了近似加法器的误差分析平台以测试各加法器的错误率及误差距离。HYB Adder的平均误差距离在所有加法器中最为优秀。本文还利用Cadence RTL Compiler来综合各加法器电路并得到其各项性能参数。从参数比较表可以看出,本文所提出的HYB Adder的速度与功耗远远优于经典精确加法器RCA。最后将近似加法器应用到DCT/ICDT的图像变换之中,重构后的图像与精确加法器重构后的图像几乎没有任何差别,由此证明了近似加法器的实用性。

