阵风扰动下大柔性飞行器姿态跟踪控制设计
吕蓉蓉,徐亮,薛辰,陆宇平
(南京航空航天大学自动化学院,江苏南京211100)
随着机载传感器和通信包近几年的迅猛发展,对能在空中长时间停留的飞行器平台的需求越来越大。大柔性飞行器可带来更好执行任务的能力,体现在更长的巡航时间、承受更重的负载、需要更好的气动性能等。能够执行军事上的侦察、收集情报等任务以及民用范围内的网络中继、气象信息采集。
Shearer和Cesnik[1-4]研究了大柔性飞行器非线性动力学和控制问题。研究提出了一种双闭环控制结构来控制简化版大柔性飞行器模型的轨迹。Gibson,Annaswamy 和 Lavretsky[5-6]将 线 性 LQR/LTR控制器与自适应LQR/LTR控制器对大柔性飞行器的稳定作用作了比较。Che,Gregory和Cao[7-8]提出了一个LQR控制器增广L1自适应输出反馈控制器的控制方案。
本文针对阵风扰动下具有不确定性的大柔性飞行器设计基于LQR的模型参考自适应控制器来跟踪其俯仰角指令。
1 大柔性飞行器模型描述
本文具体的研究对象是飞翼式柔性飞机,几何模型如图1所示。此飞翼式柔性飞机的机翼全展长有72.8 m,半弦长为2.44 m,距柔性机翼两端六分之一全翼展长处具有10°的上反角,并安置5个发动机,平均等距离坐落在翼展上。还有3个吊舱,分别位于中心和距两端六分之一展长处。飞机中心处的吊舱重约27.23 kg,可承受的有效载荷范围为0~227 kg,227 kg是其满载时的重量;两边的吊舱重约22.70 kg。机翼截面的惯性、弹性和气动特性参数如表1所示[9]。本文所用的模型是在空间柔性悬臂梁的非线性结构变形基础上,结合定常气动力模型,运用有限元法进行离散,导出其动能、势能及合外力对应的广义力,然后基于Lagrange方法推导出的大柔性飞行器非线性气弹与飞行动力学模型:
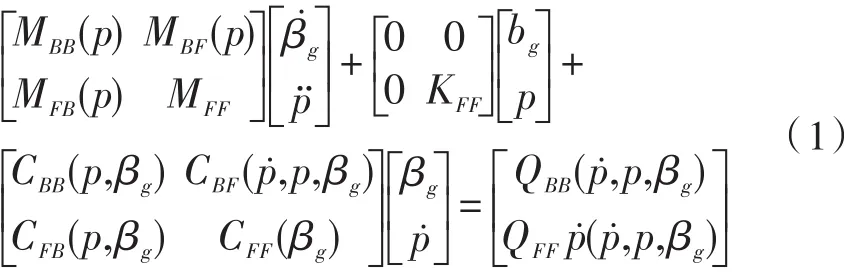

图1 飞翼式柔性飞机几何模型

表1 飞翼式柔性飞机相关参数
2 大柔性飞行器模型简化
2.1 线性化
为了方便后续大柔性飞行器控制系统的设计,需要将非线性的模型转化为线性模型。本节采用传统近似线性化方法[10],在配平求得的平衡点附近进行雅可比[11]线性化,可得到线性化系统形式如下:

经计算,该线性系统可控可观并且稳定。
2.2 模型降阶
1981年,Moore[12]提出了系统内平衡实现理论,是从可控可观性的角度对渐进稳定系统一种平衡降阶方法。其主要思想为,将系统分为强子系统和弱子系统,对部分弱可控可观的状态量进行忽略,对原模型的输入输出特性不会造成影响。这种方法的缺点是计算量特别大,但是是最常用的降阶方法之一。
考虑如式所示的线性系统,定义其可控性Gram矩阵Wc、可观性Gram矩阵Wo分别为:

由线性时不变系统完全可控可观的判据可得,当且仅当Gram矩阵Wc正定,系统完全可控;当且仅当Gram矩阵Wo正定,系统完全可观[13]。同时可以得出,Wc、Wo是以下Lyapunov方程的解:
并且,若A是渐近稳定的,则Wc、Wo是其(4)唯一的对称解。
对于线性系统(2)而言,倘若存在非奇异变换矩阵T,能将原系统转化为其等价系统,其中,该系统对应的可控性 Gram 矩阵、可观性 Gram矩阵都是相等的对角阵,即:

则称该变换T为平衡变换,原系统的平衡系统,也称为平衡实现[14]。并有为系统的Hankel阵奇异值。

平衡截断降阶法的主要思路是舍弃小于σr的Hankel矩阵奇异值所对应的状态分量,则会得到输入输出特性基本没有改变的平衡截断降阶系统模型该方法的缺点是与原系统的稳态增益有偏差,优点是能在频率范围内与原系统近似。
3 基于LQR的模型参考自适应控制器设计
3.1 线性二次型(LQR)控制器设计
因为本文要设计的是基于线性二次型(LQR)控制器的模型参考自适应控制器,所以在此之前先设计适用于飞机纵向控制的LQR控制器[15]。LQR控制器是根据被控系统的状态量以及输入量的二次积分型函数来制定一个评价函数作为衡量系统性能的指标,使得该评价函数达到最小值,从而获得系统的状态反馈矩阵。
考虑系统(2),系统性能指标的评价函数为:

其中,z为被控系统输出,zcmd为参考输出,误差e=z-zcmd。Q、R均为正定的权重矩阵。LQR控制器的设计目标是使得最优控制输入ubl之后系统的输出能够跟踪参考输出,并能使得系统性能指标的评价函数最小。Q和R矩阵一般通过试凑法得出,Q选取得越大则要求系统的误差越小,R越大则要求系统的控制能量消耗越小,两者之间相互制衡,通过选取合适的Q和R矩阵,可以使误差与控制输入达到平衡的状态。
加入姿态跟踪的误差积分:

增广系统(2),得:
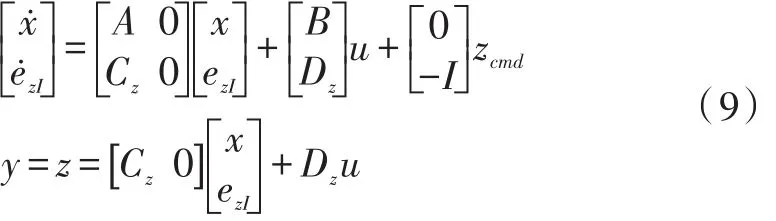
写为:


则增广系统性能指标的评价函数为:

最优控制输入为:
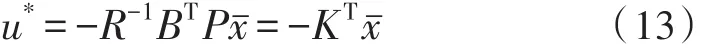
正定矩阵P满足Riccati方程:

3.2 基于LQR的模型参考自适应控制器设计
在系统(2)中加入不确定性[16-18]:
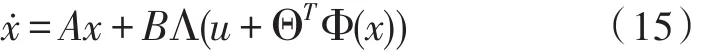
其中,u∈Rm表示系统的控制输入,x∈Rn是系统的状态量,Λ表示系统控制通道异常,为取值0到1之间的未知对角阵(0代表损坏,1代表完好)。f(x)=ΘTΦ(x)是非线性参数匹配不确定性,并且基于状态量。Φ(x)∈RN是连续的局部回归矢量,Θ∈RN×m是未知的常参矩阵。
将误差加入增广系统(15),可得:

则输出为:

对于参考模型的构建,可以使用上一节设计LQR控制器得到的状态反馈矩阵KT,该构建参考模型的方法在飞行器的姿态跟踪的自适应控制方法中应用广泛。描述参考模型为:

最终基于LQR控制器的模型参考自适应控制器的输入为:
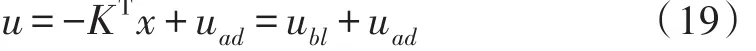
将式带入增广系统(16),可得:
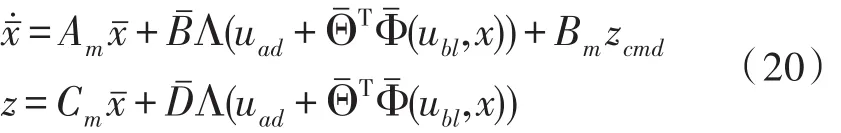
状态向量的跟踪误差为:

令控制器跟踪误差为零,则控制器输入为:

将此控制输入(22)代入增广系统(20):

状态误差的导数记为:

对于系统(22),使其渐进稳定的控制律为:

其中,自适应控制是(21),控制输入是(18),Γ,Pm是正定对称矩阵,同时Pm满足:

其中,Qm是正定矩阵。
自适应控制律中Γ为:

自适应律分解为:

模型参考自适应控制器的最终控制输入为:
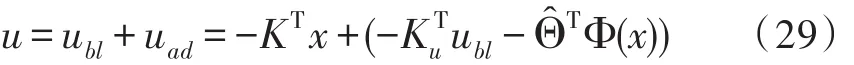
4 仿真分析
本节对Von karman紊流下的大柔性飞行器进行俯仰角跟踪。考虑不确定性,令Λ=0.7I,Φ(x)=x。初始时刻是飞行器的平衡状态下。跟踪目标zcmd在0~10 s时为 10∘,10~20 s时变为 -10∘,20 s后归零,仿真时间为30 s。
LQR控制器参数:Q=0.05I,Q(81,81)=107,R=I。
自适应增益为:Γu=10-3I,ΓΘ=10-3I。
阵风下的仿真结果如图2-4。

图2 阵风扰动下模型参考自适应控制器作用的俯仰角输出跟踪曲线

图3 阵风扰动下模型参考自适应控制器作用的操纵舵面偏角

图4 阵风扰动下模型参考自适应控制器作用的操纵舵面和发动机的控制输入
从图2仿真结果可以看出,即使在有阵风的扰动下,模型参考自适应控制器依然能良好地跟踪俯仰角。尽管在指令变化时,飞行器由于惯性作用出现了超调,但是反应时间很短,迅速地跟踪到-10∘的俯仰角。
从图3、4看出,舵面上偏,产生正的俯仰力矩,即俯仰角增大;根据牛顿第三定律,发动机产生反方向的推力,使飞行器产生抬头力矩,增大俯仰角。
5 结论
文中针对大柔性飞行器设计了一种基于LQR控制器的模型参考自适应控制器。首先,由于大柔性飞行器是一种强耦合的非线性模型,为了后续设计控制器,需要将其转化为线性系统。接着,由于大柔性飞行器建模时为了体现“柔性”而采用了有限元的思想,造成其状态空间的维数过高,给控制器的设计带来困难,所以选取平衡截断法进行模型的降阶。然后在控制器的设计中,先设计LQR控制器,再在此基础上加入了模型参考自适应控制律,仿真结果显示,即使在阵风的扰动下,其依然具有良好的姿态跟踪控制效果。

