基于宏观约束与微观放电DBD电路等效模型研究

李杰，代克杰，余亚东

（平顶山学院电气与机械工程学院，河南平顶山467000）

介质阻挡放电实质是非热平衡下的一种等离子体放电行为[1-2]。介质阻挡放电型臭氧发生器是等离子体研究最为成功的应用，以往其研究主要集中在供电拓扑结构、控制策略、负载特性和等效模型等方面，其中对等效模型的研究，是介质阻挡电路研究的核心，它为整体电路的设计提供了指导。

综合国内外学者对DBD型臭氧发生器等效模型的研究可知，这些等效模型往往基于宏观的电压、电流和放电功率的约束，忽略了臭氧发生器内部的微观放电机理[3-4]。这些模型的建立虽然极大的简化了电路的设计，但这些模型并不能反映DBD型电路的微观放电机理，不能说明宏观约束和微观放电的联系，导致了等效模型在使用时需要对某些条件进行约束，且现阶段，少有人对基于微观放电和宏观约束相结合的DBD型等效模型的研究。基于此，笔者从微观放电机理出发，首先对以往研究者们提出的DBD型臭氧发生器的等效模型进行分析；其次采用微观和宏观相结合的方法推导出本文的DBD型电路的等效模型；最后给出了本文等效模型的实验验证结果。

1 DBD型电路宏观等效模型

DBD型负载在交流电压作用下，存在放电和未放电两种状态。当DBD电路处于未放电状态时，可以看成为介质阻挡电容Cd和气隙电容Cg相串联的电路结构[5-6]；当其处于放电状态时，其可等效为介质阻挡电容Cd和一个与外加电压相反的电压UZ（放电维持电压）相串联的结构[7]；图1给出了在放电过程中的DBD负载的等效电路。该电路模型由于参数不连续，且对供电电源设计极为不便，也未能解释划分这两种状态的微观原因，渐渐的淡出人们的视野。

图1 由DBD负载放电过程得到的等效电路

为此许多学者提出了参数连续型的等效模型。如图2所示，J.Marcos Alonso等人认为DBD型电路在一定范围内可用一数值恒定电容与电阻并联的电路来进行等效的电路模型[8-9]；V.H.Olivares等人则给出了DBD型臭氧发生器可以用一个电阻与电容串联的电路来进行等效的电路模型[10-11]。

图2 DBD负载的参数连续型等效模型

以上模型都是基于DBD负载的电压、电流和放电功率等宏观放电参数而言的。现阶段，DBD型电路的等效模型的水平仅限于此。通过宏观约束获得的DBD型电路的等效模型并不能解释为什么是这样的约束关系，其原理如何，等离子体的放电机理是如何，笔者带着这些问题对DBD型电路深入的研究，通过宏观约束与微观放电相结合的方式得到DBD型电路的等效模型。

2 DBD型电路的微观等效模型的研究

2.1 介质阻挡等离子体放电特征

文献[12]指出物质由微观粒子构成。当给物质施加高温和高能量时，物质就会电离为电子、离子和自由基；当能量很高时物质会变成带正电和带负电的粒子，此时施加电场，就会形成电流。图3给出了等离子气体放电伏安特性曲线。

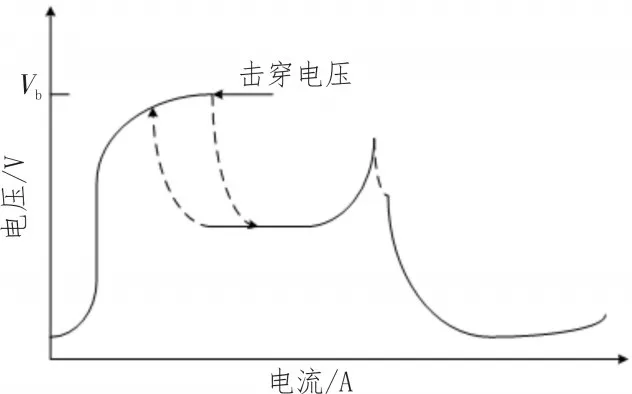
图3 介质阻挡等离子气体放电伏安特性曲线

从图3中可以看出，在气体放电初期，放电电流呈快速增大趋势，而电流变化与电压变化不成正相关关系；同时还可看出放电电流基本在某个电压等级下或者在某一个临界值后呈现线性增长的趋势。出现此种情况，可以通过等离子体的微观碰撞来描述。

依据汤森放电定律，设每个电子沿电场方向移动1 cm距离时，与气体分子或原子碰撞所能产生的平均电离次数为α，α叫汤森第一电离系数[12]。其满足式（1）：

式中p为气压，E为电场强度，A，B是与气体相关的常数。

假定单位面积气体厚度为dx，有n个电子通过，则新增的电子数满足式（2）:

设放电气隙距离为dcg，每秒从阴极发出的电子数n0，对式（2）积分得:

通过求解式（3），同时在等式两边同时乘以电子电荷量q则可以得到式（4）：

则可以得到气体放电电流为式（5）：

式中I为放电管中电流，I0为饱和电流，α为汤森第一电离系数。

2.2 DBD型电路微观等效模型数学公式推导

以往获得等效模型的思路是研究宏观参量的约束进而获得等效模型。DBD宏观特征的实质是微观机理量变的表现。基于此，从微观研究获得的等效模型能够从根本上解释宏观特征，理论上能够得到更为普适的等效模型。DBD放电现象属于非热平衡下等离子体放电，同样具有等离子体特征。

从宏观和微观相结合的方法入手，根据DBD型负载电路的工作过程，能够得到DBD型臭氧发生器的简化版等效电路如图4所示。笔者为简化讨论，以正弦交流电压的正半周期为基础来讨论在该电压下的DBD型电路的微观等效模型的数学公式的推导。

图4 DBD型臭氧发生器的简化等效电路

图中uAC为折合到变压器副边的电压，i(t)电路系统中总电流，icd为等效的介质阻挡电流，icg为等效的气隙电流，idis为气体的放电电流，R为等效的气体放电电阻，Rg为等效的气隙电容的阻抗。那么根据图4的电路结构得到如式（6）所示的电路约束公式。

由介质阻挡放电的电场强度与介电常数的比值可得：

式中Ed为介质电场，Eg为气隙电场，εd为介质介电常数，εg为气体介电常数，dd为介质厚度，dg为气隙电场距离。则有：

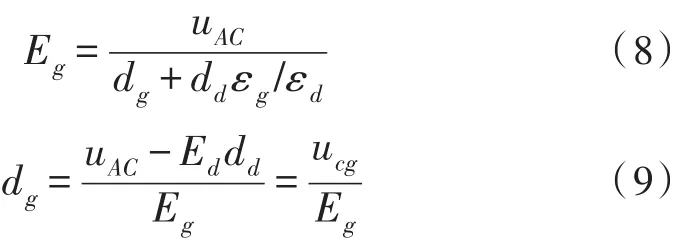
由上述介绍的介质阻挡等离子体放电特征可知：

由式（7）（8）（9）可将式（10）简化为：

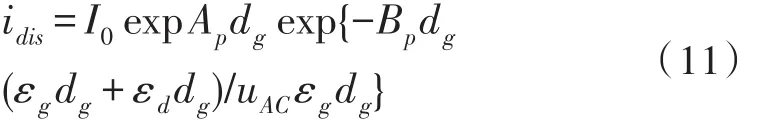
在式（11）中只有uAC是本结构中的一个变化量，求得uAC就可求得DBD型电路未击穿时的电流。故，可将式（11）简化为：

其中，m=I0、j=Apdg、

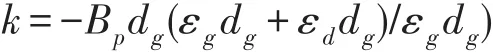
结合式（6）可得：

以往研究者认为DBD电路在发生放电击穿后，放电间隙的电压在小范围内波动，放电气隙电容不变[12-13]。故笔者在分析微观等效模型的数学推导过程中也将气隙电容视为一固定值，则式（13）进一步化简为：

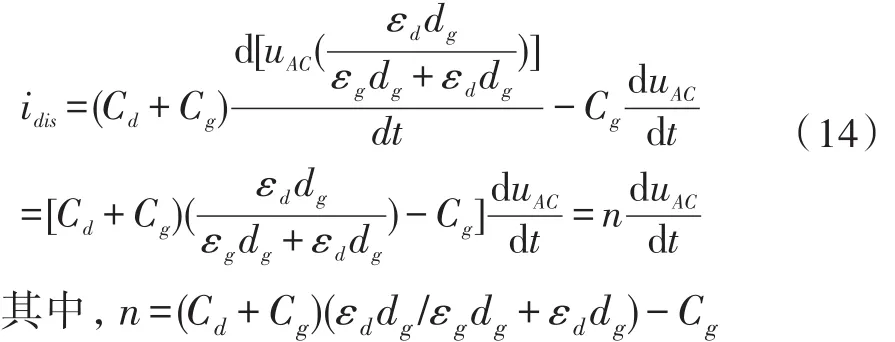
式（14）中，Cd为一固定不变的介质阻挡电容常量；Cg为一固定不变的绝缘介质常量。前文已视uAC是一变量，当DBD型电路放电时，放电电流的大小只和uAC有关。同时还可以看出，放电击穿后，放电的其他参数与放电气隙的容性效应无关，此时可认为微观放电强烈，放电气隙呈现出导电流体的阻性特性。故笔者认为从微观机理出发可以将DBD型臭氧发生器等效为一个电容和电阻的串联电路。

3 DBD型电路等效模型的提出及验证

3.1 DBD型电路等效模型的提出

基于2.1和2.2小节，从微观和宏观两方面入手，推导介质阻挡放电电流与外加电压的关系，从而把微观和宏观联系起来。笔者从微观和宏观角度考虑认为DBD型臭氧发生器电路可用等效电阻和电容串联进行等效（其放电功率成线性关系），其数学表达式为式（15）所示：

式中，Rp和Cp为DBD型臭氧发生器等效电阻和等效电容；P为臭氧发生器放电功率；MR、NR、MC和MC为臭氧发生器电极形状、阻挡介质材料等相关的常数。

3.2 DBD型等效电路的实验验证

为有力的验证笔者从微观和宏观角度考虑提出的DBD型臭氧发生器电路的等效电路的正确性，笔者搭建了实验平台，从多角度验证笔者提出的等效模型的合理性。本文采用全桥逆变拓扑结构[14-15]作为DBD型电路的供电拓扑。实验平台如图5所示。

图5 实验平台

图6 李萨茹图形实验波形

文中采用李萨茹图形测量法[16]对DBD型臭氧发生器负载参数进行测量，图6给出了李萨茹实验波形，通过对李萨茹图形关键点的求取来获得DBD型电路的参数值。图7（a）、7（b）分别给出了不同条件下DBD型臭氧发生器的比电阻、比电容与比功率的拟合曲线图。

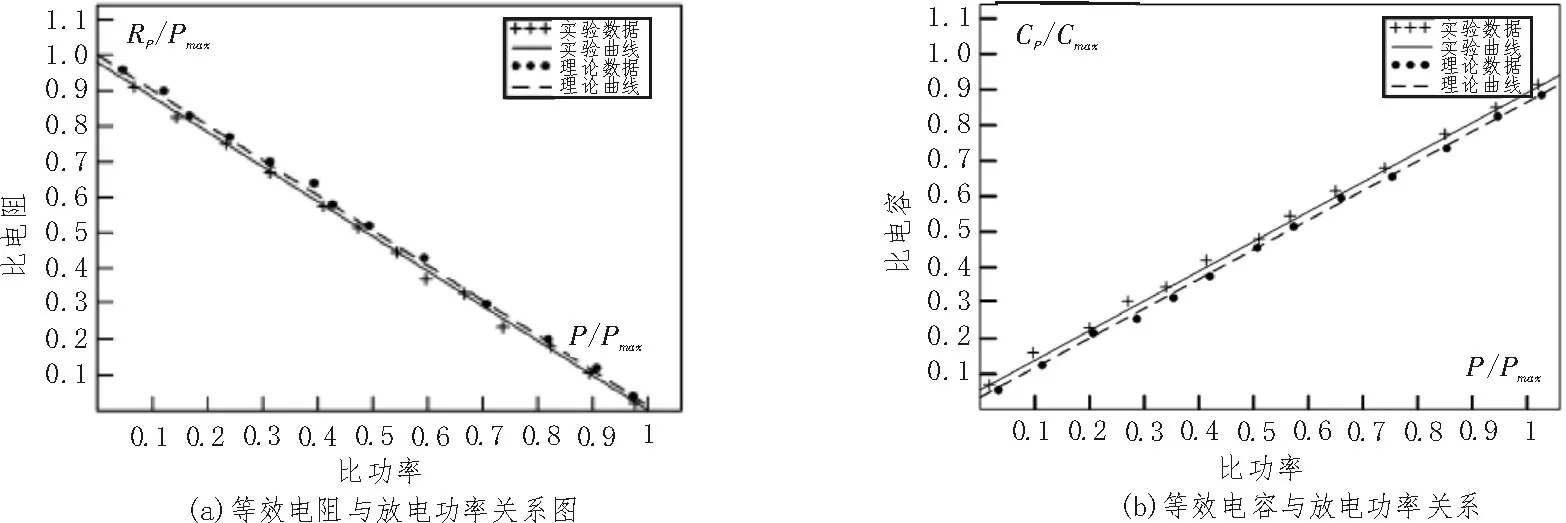
图7 等效电阻、电容与放电功率拟合曲线图

注：图7中的比电阻、比电容、比功率分别为Rp/Rmax、Cp/Cmax、P/Pmax，其中P、Pmax分别为发生器的实际放电功率与额定放电功率；Rmax和Cmax分别指放电功率为Pmax时发生器的等效电阻和等效电容。

由图7可以看出，等效电阻与放电功率呈负相关；等效电容与放电功率成正相关。且从图中可知拟合值与实验值的误差小于4%。故，将DBD型电路等效为与放电功率有关的电阻和容抗串联的等效电路是正确的。为进一步验证笔者提出的等效模型的正确性，笔者在不同电压等级下得到了DBD电路的等效电阻和等效电容的拟合值与实验值的误差（表1）。

表1 不同电压等级下等效电阻和等效电容的拟合值与实验值的误差

通过对DBD型臭氧发生器电路的不同条件下的实验结果的分析，验证了从微观和宏观相结合所得到的DBD型电路用阻容式电路替代的结论的正确性，且验证了在微观放电机理下所推导放电电流与外加交流电压的约束关系（即式（14））的正确性。

4 结论

文中结合以往DBD型电路等效电路的研究结果，从宏观和微观角度深入研究了DBD型臭氧发生器等效模型。基于等离子体的相关特性，从DBD型电路的微观放电机理入手，通过数学公式的推导得到了DBD型电路的放电电流和外部激励电压的相互关系；最后在实验平台下对宏观条件下的DBD型臭氧发生器电路进行分析，在不同实验条件下验证了在微观和宏观相结合的方法下所提出的等效模型的合理性。