分段式高性能近似加法器设计

李凯磊,杨文强,王伦耀

（宁波大学 信息科学与工程学院,浙江 宁波 315211）

在数字电路设计中,逻辑正确是设计的首要目标.但在实际应用中,如涉及图像、音频处理等多媒体应用方面,因人类感知能力限制,即使存在一定范围内的错误输出,也不影响人们的视听效果.实际应用中的容错特性为逻辑电路的优化提供了一条新途径.利用近似计算技术实现电路逻辑优化,其本质就是通过降低电路的输出精度来实现电路简化,进而达到电路的功耗、面积或者时延等性能指标的优化.

在集成电路设计中,加法器是一种被广泛应用的电路单元,加法器性能与整个系统性能关系密切.高性能加法器设计一直是学术界和工业界高度关注的问题[1-2].在误差允许的情况下,引入近似加法器是提高加法器性能的一种有益尝试.考虑到近似加法器的输出误差与发生错误输出位的权重有关,权重到高的输出位发生错误将引起更大的误差,并且输出误差的大小也是近似加法器设计过程中一个关键指标,为此本文提出了一种三段式加法器设计,该设计基本思想是在低权重输出位用简单的逻辑门,甚至常数来代替全加器,而在高权重部分则采用精确加法器来实现,从而在误差大小与电路性能之间实现折中.

1 相关工作

1.1 研究现状

已有的近似加法器在结构上大致分为二段式和多段式两种类型[3].

二段式近似加法器包含两部分,即由精确加法器构成MSB(More Significant Bits)部分,以及由近似加法器构成的LSB(Less Significant Bits)部分,其中,LSB 部分一般采用无进位近似加法器.此类近似加法器的每一位都单独进行运算,不产生或接收进位信号,因而可以减少因进位产生的延时,进而提高电路的运算速度.

二段式近似加法器的这种结构可以在增加有限输出误差的情况下,实现电路面积、延迟以及功耗等优化.现有的低位或门加法器(Lower Part OR Adder,LOA)[4]、容错加法器I(Error Tolerant Adder-I,ETA-I)[5]等均为二段式近似加法器.

其中,ETA-I 加法器的精确部分由行波进位加法器实现,近似部分每一位求和运算全部使用XOR模块代替.该模块在第i位输入Ai和Bi分别在“00”“01”或“10”的时候进行正常XOR 运算;而在“11”的时候,从第i位开始至最低位,求和的输出结果全部被设置为“1”.此类加法器的输出误差比较小,但因其高位部分由传统的精确加法器构成,且通过XOR 门以及控制模块组成低位,因此相对于某些近似加法器电路,其电路面积开销较大.

现有多段式近似加法器包括精度可配置加法器II(Accuracy Configurable Approximate Adder-II,ACA-II)[6]、容错加法器II(Error Tolerant Adder-II,ETA-II)[7]、预测进位选择加法器(Speculative Carry Select Addition,SCSA)[8]和通用精度可配置加法器(Generic Accuracy Configurable Adder,GeAr)[9]等.多段式加法器一般由多个并行子加法器模块组成,每个子加法器模块分为MSB 部分与LSB 部分.其中MSB 部分用于输出一部分求和结果,LSB 部分用于预测进位信号,并传递给MSB 部分,不用于求和计算.最后所有子加法器MSB 部分的求和结果组合起来即为此类近似加法器的最终求和输出.此类多段式加法器虽然可以显著降低延迟,但是因其由多个子加法器模块构成,电路面积相较于其他近似加法器增加很多.

ETA-II 加法器结构如图1 所示,n位加法器被分割成m个子加法器模块,每个模块中包含1 个k位行波进位加法器(Ripple Carry Adder,RCA)模块,以及1 个k位超前进位加法器(Carry Lookahead Adder,CLA)模块,分别用于2 个加数对应字段求和以及进位信号预测.

图1 ETA-II 加法器

从图1 可知,ETA-II 多段式加法器第h个子加法模块的进位仅仅与当前k位输入和第(h-1)个子加法模块的k位输入有关,1 ≤h≤ (m-1),因此该加法器可以将进位链深度由原来的n缩短到2k,进而显著减小电路时延.但同时因进位链被截断,使得在某些输入组合下,ETA-II 会产生很大的误差.以图2 所示12 位加法器为例,该加法器包含3 个子加法模块,本文称之为ETA-II-3 加法器.当输入2 个12 位的加数为A[11:0]=“000011111111”(255)和B[11:0]=“000000000001”(1)时,由于处于高位子加法模块的进位来自于次高位子加法电路的进位输出,在图2 所示的输入组合时,次高位子加法电路的进位输出为0,导致该12位加法器最终的输出为0,而不是256,产生很大误差.

1.2 计算误差评价指标

近似加法器的计算误差通常采用误差距离(Error Distance,ED),以及与误差距离紧密相关的平均误差距离(Mean Error Distance,MED)、相对误差距离(Relative Error Distance,RED)、平均相对误差距离(Mean Relative Error Distance,MRED)和归一化误差距离(Normalized Mean Error Distance,NMED)等指标来衡量[10].

误差距离(EED)定义为近似加法器所获得的值与正确结果之间差值的绝对值.式(1)中Rc和Re分别表示正确值和近似值,且均用十进制表示:

平均误差距离(EMED)为α个误差距离取平均值:

相对误差距离(ERED)是误差距离与正确值比:

平均相对误差距离(EMRED)为α个相对误差距离取平均值:

归一化误差距离是平均误差距离的归一化:

加法器精度(Accuracy,ACC)表示特定输入的输出“正确”程度,其值范围为0%～100%,定义为:

最低可接受精度(Minimum Acceptable Accuracy,MAA)表示近似加法器输出结果精度最低的百分值,而可接受结果概率(Acceptance Probability,AP)是指加法器精度高于最小可接受精度的概率,0≤AAP≤1:

2 三段式高性能非精确加法器

2.1 三段式低功耗非精确加法器介绍

本文提出的三段式n位高性能非精确加法器结构如图3 所示,n=4z,z∈ {1,2,3,4,…} .该近似加法器被分割成三部分.第一部分为加法器低位部分,位宽为n/4,这部分每一位的输出结果被设置为常数“1”,也称为CON 块;第二部分为加法器中间部分,位宽为n/4,用一个二输入逻辑门代替一位全加器,这部分电路也称TP 块.剩余部分为精确计算部分,由RCA 构成.

图3 三段式高性能非精确加法器结构图

2.1.1 CON 块

CON 块为常数块,即无论A[n/4 -1:0]和B[n/4 -1:0]输入什么值,输出结果S[n/4 -1:0]将全部被置为常数,这样将使延迟、面积和功耗得到大幅度降低.由于平均误差距离是衡量近似加法器的一个关键指标,CON 块的常数输出设置应该尽可能引入较小的平均误差.

设A、B为2 个加数,A、B为整数,且0≤A≤K-1,0 ≤B≤K-1.则A、B可以产生K2种输入组合.设Si为其中一种输入组合的和,0≤i≤(K2-1),则所有输入情况下加法器输出的求和结果为:

因此,其求和的平均值为:

显然,对于位宽为n/4的CON 块,为了使CON 块对应的平均误差距离最小,CON 块的输出应该为 2n/4-1,即置CON 块的所有输出为“1”.

2.1.2 TP 块

TP 块输出结果S[n/2 -1:n/4]由A[n/2 -1:n/4]和B[n/2 -1:n/4]的每一位单独进行基本二输入逻辑运算所得,且每一位不产生也不接收任何进位信号,从而减少电路面积和时延.

从表1 可知,XOR 门的输出与加法器的求和输出一致,但没有进位信号;OR 门的4 个输出中有3个与加法器的输出一致,而AND 门只有1 个输出与加法器的输出一样.因此,在TP 块中不考虑AND 门.

表1 TP 块逻辑门选择与半加器结果比较

相比OR 门,虽然在4 个输入组合中,XOR 门的输出均与加法器和的输出一样,但由于在TP 块中各位之间没有进位,因此在2 个加数的某一位输入均为“1”时,XOR 门的输出实际上是“0”,而OR 门的输出为“1”,反而OR 门引起的误差更小.另外,对于二输入OR 门而言,只有其中一个输入为“0”时,另一个的输入变化才能引起输出变化,而二输入XOR 门的任何输入变化都会反映到输入端,因此相比OR 门,XOR 门对输入的变化更敏感,其动态功耗也将更大.此外,XOR 的电路面积要比OR 门大.在本文中,将同时给出OR 门和XOR 替代全加器后的电路性能比较结果.

2.1.3 RCA 块

三段加法器的高位部分由精确加法器组成.对于一个n位二进制,其对应的十进制可表示为:

从上式可知,由于高位权重大于低位权重,因此同样某一位上出错,高位错误引起的误差会更大,这也就是TSA 加法器在高位采用精确加法器的原因.本文设计中,高位部分采用行波加法器,此类加法器结构简单,但进位链长.由于本设计中将进位链进行了截断,长度只有原来的一半,因此可有效减少整个电路的时延.

2.2 三段式非精确加法器误差分析及改进

由图3 结构可知,该近似加法器产生误差的情况均取决于TP 块和CON 块.相比与CON 块,TP块在图3 的结构中处于高位段.因此TP 块和CON块引起误差的大小主要由TP 块决定.

从表1 可知,在二进制加法中,某一位的2 个加数的4 种输入组合中,当TP 块中的二输入逻辑门采用XOR 门时,求和输出均正确,但是在输入组合为“11”时,没有产生进位.当TP 块中的二输入逻辑门采用OR 门时,在输入组合为“11”时,求和输出错误,同时没有产生进位,其他3 种输入组合均正确.从上面分析不难看出,TP 块产生的求和输出结果小于正确值.为减少TP 块的误差距离,本文将TP 进行了如下改进.

假设TP 块长度为L,则将第位的二输入逻辑门输出用常量“1”来代替.同时,考虑到TP 块最高位为“1”时,肯定会产生进位输出,因此将TP 块结构改进为图4 所示结构.

图4 改进后TP 块结构图

表2 为在位宽为16 位情况下,图4 结构的TP块与图3 结构的TP 块在随机输入情况下与正确值的错误误差比较结果.

表2 修改后16 位TP 模块加法精度比较

表2 中,TPOR和TPXOR分别表示TP 块中二输入逻辑门采用OR 门和XOR 门后电路的各性能参数,TPOR-1和TPXOR-1分别表示采用图4 结构后的电路性能参数.并且表2 中,各误差参数是在随机产生105种输入组合,利用MATLAB 模拟得到.面积和功耗参数利用Design Complier 在fast_1v32c0 工艺库下得到.

通过表2 可知,在8 位宽下,TP 块采用OR 门所产生的计算误差相较于采用XOR 门要小,且在电路功耗和电路面积方面的表现也比采用XOR 门要好.采用图4 结构的TPOR-1与仅由OR 门构成的TPOR相比,在计算精度和减小电路开销方面均有提升.

结合表2 的结果,本文提出的近似加法器的结构如图5 所示,并称该电路为TSA 加法器.其中,在TP 块中采用二输入OR 门.

图5 TSA 加法器结构图

3 实验结果

本节将对文中提出的近似加法器与几种经典的近似加法器在面积、延迟、功耗和精度等方面的特性进行比较.为获得加法器电路的面积、功耗和时延数据,先将近似加法器用Verilog HDL 语言描述,然后用Design Complier进行综合得到,其中综合过程中用到的工艺库为fast_1v32c0.表3 即为实验结果.

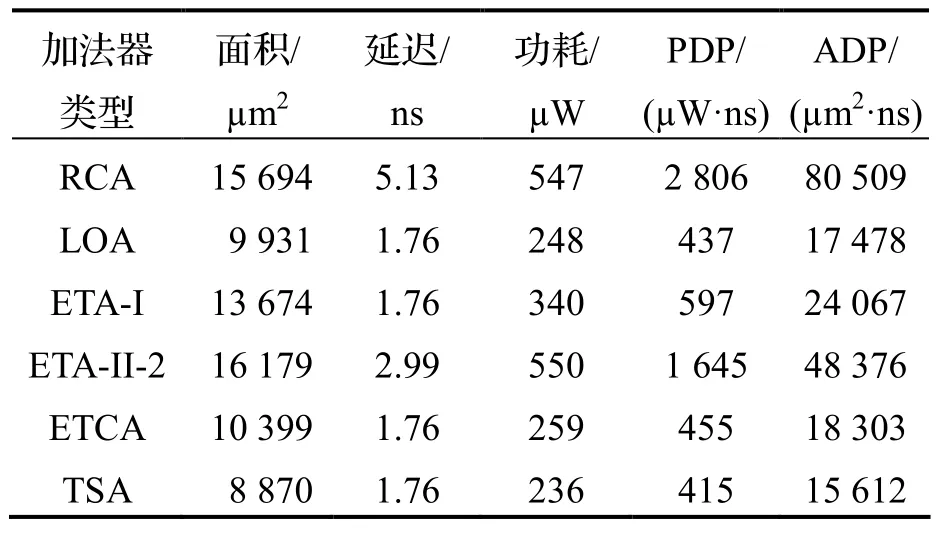
表3 各16 位加法器电路性能比较

表3 中,近似加法器LOA、ETA-I、ETA-II-2、ETCA[11]和TSA 的加数位宽均为16 位,且高8 位均采用RCA 精确加法器.从表中可以看出,本文所提出的TSA 近似加法器总体性能较好.由于TSA 中间部分采用部分精确电路,通过OR 门代替一位全加器,低位部分每一位输出结果都被设置为常数1,这种设计有利于TSA 在面积、功耗和时延上的优化.相较于RCA 面积、功耗、功耗延迟积(Power Delay Product,PDP)和面积延迟积(Area Delay Product,ADP)分别下降约43%、57%、85%和81%.与ETCA 相比,TSA 加法器在面积、功耗和面积功耗积方面分别有大约15%、9%、22%的改善,相对于LOA、ETA-I、ETA-II-2 各方面都具有不同程度的提高.由于上述电路均采用进位链截断技术,进位链长度相仿,因此各电路的时延均接近.而ETA-II-2 由于将求和运算与进位信号预测分为两部分,导致时延比较长.

计算误差是衡量近似加法器的一个关键指标.本文中各近似加法器的计算误差是利用MATLAB对各近似加法器进行建模,并输入105个随机数进行仿真获得.表4 即为各近似加法器计算误差仿真结果.

表4 各16 位加法器计算误差比较

不难看出,TSA 近似加法器因TP 块采用OR门,低位部分直接被置为“1”,其计算误差与ETCA 和ETA-I 相比略有增加,但相较于ETA-II-2和LOA 在平均误差距离、归一化误差距离以及平均相对误差距离均有改进,其中与ETA-II-2 相比,上述指标分别提高了约52%、52%和67%.

对不同位宽的TSA 加法器和MAA 下AP 的仿真结果见表5.对于不同MAA(MAA＜100%)值,位宽越大,其AP 值越趋近于100%,因此本文所提出的加法器在位宽较大的加法计算中也具有极大优势.

表5 不同位宽和MAA 下TSA 加法器的AP 值 %

4 总结

由于加法器的计算误差大小与错误发生的位置关系密切,相比于权重大的输出位发生错误,权重小的输出位错误引起的误差要小很多.针对加法器此特点,本文三段式近似加法器将加法器分成三段,其中权重高的段用精确加法器实现,达到降低误差目的,中间和低位部分采用OR门和常数,且各位之间不存在进位关系.这种设计显著降低了电路面积和功耗,同时也对计算误差与电路性能改善进行了折中.与传统精确加法器行波进位加法器相比,该加法器的面积、功耗、功耗延迟积和面积延迟积分别下降约43%、57%、85%和81%.与现有分段式近似加法器相比,总体性能有明显改善.