一种低开销的近似乘法器设计
谢迎娟,折夏煜,褚嘉敏,王 亮,蔡 莉,王海滨,韩光洁
1(河海大学 物联网工程学院,南京 211100) 2(北京微电子技术研究所,北京 100076) 3(中国科学院 近代物理研究所,兰州 730000) 4(江苏省输配电装备技术重点实验室,江苏 常州 213000) E-mail:wanghaibin@hhu.edu.cn
1 引 言
在过去的几十年里,各种先进的计算系统得到广泛的开发和应用.超级计算机日新月异,各类计算中心和服务器无处不在,已经深度融入人类生产生活的方方面面.但与此同时,一方面,传统的计算系统在一些重要的物理限制(如功耗、面积等指标)下不能有效地进一步增强性能,摩尔定律已经接近极限;另一方面,对于一部分产业来说,计算系统需要得到精确的结果[1],但在越来越多的应用系统中,并不需要严格意义上的正确结果.例如,图像处理算法的计算通常在像素级进行,轻微的质量缺陷是可以容忍的,人类视觉系统无法察觉.人们越来越认识到,过度的精确性从来就不是免费的,它消耗了我们的时间和世界的能源.因此,通过牺牲不必要的精度,可以在功率和性能上获得极大的优化.
近似计算(Approximate Computing)利用计算结果的准确性来优化系统资源的使用,是加速处理器的最可行方法之一[2].对于许多可以接受不准确结果的系统来说,如人工智能、机器学习[3]、数字信号处理(Digital Signal Processing,DSP)、多媒体、机器学习和模式识别[4]等,它已经成为一种比传统计算架构更可取的新方案.受人脑容错能力的启发,近似计算在不牺牲功能和“感知”的情况下通过适当地降低计算精度,来协调和权衡计算质量(例如,精度)和计算消耗(例如,功耗和面积)[5].
近似计算可以应用于硬件和软件以及不同的系统层[6].在电路级,由于其在许多计算应用中的重要作用,近似算法单元的设计得到了广泛的研究.近些年来,各种近似加法器已经被提出,以达到降低功耗和延迟的目的.而相比于加法器,乘法器的结构更加复杂,面积和功耗往往是同位宽加法器的数倍,因此近似乘法器对性能的优化更加可观.相比于精确乘法器,近似乘法器通过适当地放宽运算精度,简化或删除部分运算电路,不仅可以节省开销,并且能够优化电路中关键路径的延时,加快计算速度[7].对于一些处理过程本身就是不精确的应用来说,近似乘法器甚至可以对原有的不精确部分进行补偿,得到更好的处理结果.
本文基于精确二进制乘法器,提出了操作数裁剪模块和低开销部分积累加算法,设计了一种新型近似乘法器.并对该近似乘法器的误差特性和开销性能进行仿真,与主流输入级近似方法进行对比.
2 相关工作
一般地,在数字电路中,近似计算可以运用于近似乘法器的3个部分:
1)输入级近似:
通过编码或者直接截断的方式,减少了部分积的产生和运算过程.1962年,J.N.Mitcheu提出了对数乘法器,即将两个二进制乘数通过以2为底的对数运算转化为其近似的二进制对数,再通过加法器将二者相加,最后将和还原为近似积[8].但是将数字转化为近似对数时较为麻烦,导致功耗增加.迭代对数乘法器(Iterative Logarithmic Multiplier,ILM)是以精度为代价对其进行改进的简洁算法,但是误差比对数乘法器大.G.Zervakis等人利用部分积穿孔技术实现了乘法运算的近似,并以穿孔位置及大小为变量对近似乘法器的精度和开销进行了分析比较[9].S.Vahdat等人提出了基于截断和舍入的动态近似乘法器(Truncation-and Rounding-based Scalable Approximate Multiplier,TOSAM),获得了较高的精确度,但是功耗降低的程度有限[10].S.Narayanamoorthy等人提出的加强型静态片段法乘法器(Enhanced Static Segment Multiplier,ESSM)主要思想为采用多个固定片段,当判断高位的片段为全0时采用下一个片段[11].另外,动态范围无偏乘法器(Dynamic Range Unbiased Multiplier,DRUM)[12]和基于取整的乘法器(Rounding-Based Approximate,RoBA)[13]也是两种误差较小的近似算法,但是面积与功耗较大.其中,DRUM引入了最高有效位检测模块(Leading-One Detector,LOD),动态地对最有效的位进行乘法运算.
2)部分积产生级近似:
通过在相乘的过程中避免低位部分积的产生,从而减少相乘的运算步骤.生成部分乘积的一种简单方法是将乘数的每一位乘上被乘数,这可以通过简单的逻辑运算来实现.另一种方法是将乘法器编码为高基数,并将已编码的乘法器乘以被乘数.随着基数的增加,对乘法器的编码就变得更加复杂.因此,为了降低复杂度,可以使用近似编码器来生成部分乘积[14].W.Liu等人提出了两种有效的以4为基数近似Booth编码器[15].
3)部分积求和级近似:
通过对重要位(即高位)精确求和而对不重要位(即低位)近似求和,从而缩短进位链,减小延时开销.H.R.Mahdiani等人提出了一种不精确的阵列乘法器,将部分积树中一些最不重要的列作为常数忽略掉[16].另外,在高速乘法器的设计中,压缩器或计数器被广泛用于加速部分积的求和.O.Akbari等人提出了4种近似4∶2的压缩器并运用于乘法运算中[17].M.Ha和S.Lee提出了一种近似4∶2的压缩器,并在部分积累积步骤中引入了误差恢复模块,提高了乘法的精度[18].
本文将针对乘法器的输入级,设计新型近似乘法器,并与主流近似乘法器进行比较.
3 近似乘法器实现
3.1 精确二进制乘法器
精确乘法器的二进制运算流程如图1所示.其中,操作数A和操作数B为乘法的输入项的二进制表示,可写为:
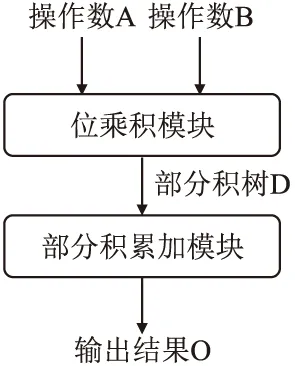
图1 乘法器的运算流程Fig.1 Operation flow of the reference multiplier
(1)
(2)
其中,n1、n2分别是储存两个二进制操作数A、B的寄存器位宽,ai、bi分别是二进制操作数A、B从低位开始第i位的值(i≥0).
对于位乘积模块,本文采用将乘数的每一位乘上被乘数的逻辑运算方法生成部分积树.对部分积树进行累加,得到乘积的二进制输出O:
O=A×B
(3)
3.2 基于穿孔的近似乘法器
一般地,将操作数中2的指数越大的位称为高位,反之为低位.高位为重要位,即高位被更改比低位对乘法结果的影响更大.
基于穿孔的近似乘法器从低位开始舍去操作数的部分位,在可接受精确度范围内减少部分积累加步骤.通过改变穿孔起点和长度,实现运算精度和开销之间的权衡.
在该近似乘法器中,设置操作数的穿孔起点及长度分别为j、k,则穿孔后进行位乘积的输入项为:
(4)
(5)
生成部分积树后,进行累加,得到乘积的二进制输出Oq:
Oq=Aq×Bq;
(6)
3.3 基于操作数裁剪的新型近似乘法器
本节将基于精确乘法器的二进制运算流程,提出操作数裁剪方法和低开销部分积累加算法,设计一种新型近似乘法器.运算流程图如图2所示,通过以下4步实现:
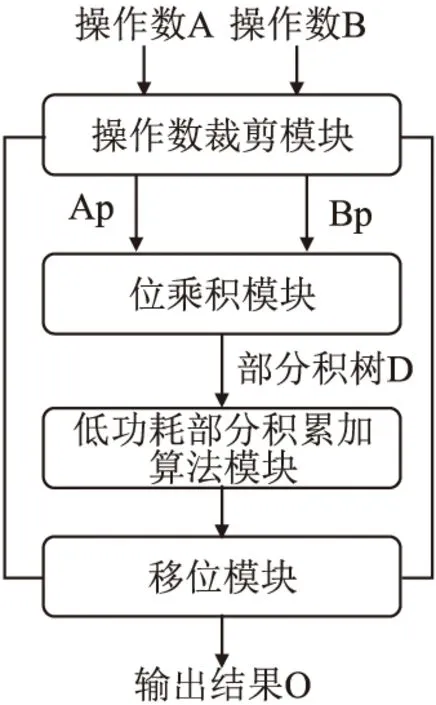
图2 基于操作数裁剪的近似乘法器运算流程Fig.2 Operation flow of the proposed approxiamte multiplier
1)操作数裁剪
操作数A和B操作数为该近似乘法器的输入项.
首先,根据储存两个二进制操作数A、B的寄存器位宽,设置分别对A和B进行近似操作的截取间隔数k、l(k、l为正整数).
根据截取间隔数k、l确定A和B的近似标志位,设A的近似标志位:
Ac=or(a2k+2,a2k+3,…,an1-1)
(7)
记B的近似标志位:
Bc=or(b2l+2,b2l+3,…,bn2-1)
(8)
其次,根据近似标志位Ac、Bc确定简化的乘法输入项.图3为对操作数A进行截取操作的示意图.
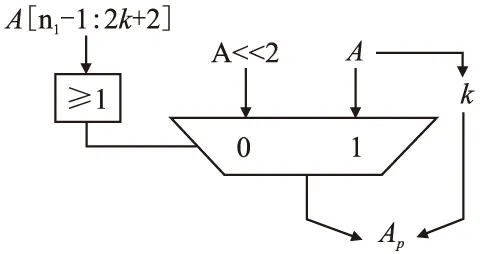
图3 操作数截取操作示意图Fig.3 Diagram of operand pruning
若Ac=0,表示二进制操作数A从低位开始的第2k+2位-第n1-1位均为零,则将A左移两位;若Ac=1,表示二进制操作数A从低位开始的第2k+2位-第n1-1位不全为零,则不对A进行移位操作.
最后,对二进制操作数A的第0位-第2k-1位进行近似截取操作,保留第0位及第k位,去除第1-第k-1位及第k+1-第2k-1位,共去除2k-2位,同时更新第2k位的值a′2k,得到简化的乘法输入项Ap,表示为:
(9)
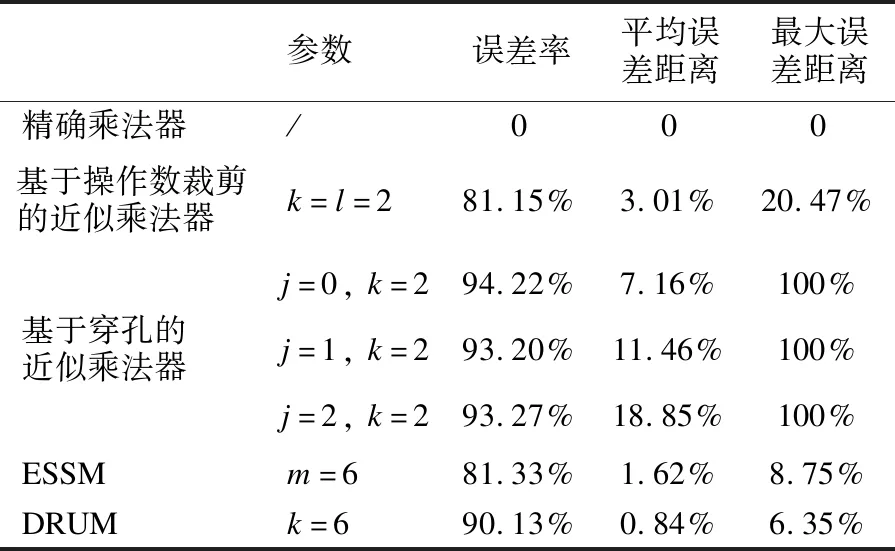
其中,当0 a′2k=or(and(a2k-1,ak-1),a2k) (10) 当k≥3时, a′2k=or(and(a2k-1,a2k-2),a2k) (11) 同样地,对B进行移位和截取操作. 若Bc=0,表示二进制操作数B从低位开始的第2l位-第n2-1位均为零,则将B左移两位;若Bc=1,表示二进制操作数B从低位开始的第2l位-第n2-1位不全为零,则不对B进行移位操作. 对二进制操作数B的第0位-第2l-1位进行近似截取操作,保留第0位-第l位,去除第1-第l-1位及第l+1-第2l-1位,共去除2l-2位,同时更新第2l位的值b′2l,得到简化的乘法输入项Bp,表示为: (12) 其中,当l<3时, b′2l=or(and(b2l-1,bl-1),b2l) (13) 当l≥3时, b′2l=or(and(b2l-1,b2l-2),b2l) (14) 2)位乘积 通过位乘积模块,得到部分积树.同样地,该模块生成部分乘积所使用的方法是将乘数的每一位乘上被乘数,通过简单的逻辑运算来实现. 3)部分积累加 当对部分积进行累加时,记部分积树的第m行部分积为Dm(m=1,2,…,P). 累加的具体操作为:首先,分别利用全加器和半加器对D1、D2、D3、D4按位进行累加操作,得到新的部分积D′3和D′4;然后分别利用全加器和半加器对D′3、D′4、D5按位进行累加操作,得到新的部分积D″4和D″5;重复累加操作,直到所有部分积都累加完成得到最终乘法结果O,O为二进制操作数. 需要注意的是,累加操作一共执行P-2步,其中第一步后部分积减少两行,其余P-3步后部分积每次减少一行. 4)移位 在输入项截取模块中,根据近似标志位Ac、Bc的大小确定是否对A、B进行移位操作.因此,在部分积累加模块后,需要根据Ac、Bc的大小对部分积累加结果进行移位操作,得到最终的乘积输出Op: Op=Ap×Bp (15) 以8位乘法器为例,分析精确和近似乘法器的开销. 对于精确乘法器,通过位乘积运算得到的部分积树共有8行.图4(a)为对部分积树进行累加的过程简化图,其中一个黑点代表一个数据,如图例所示,虚线框内包含两个数据的为加法器,加法器内包含3个数据的为全加器. 由图4(a)可得,基于部分积树,每一步运算后部分积减少一行.因此,8位精确乘法器一共需7步计算得到最终的结果. 对于基于穿孔的近似乘法器,设置j=0,k=2,则位乘积运算得到的部分积树共有6行,图4(b)为累加操作的简化过程.基于部分积树,基于穿孔的近似乘法器一共需要5步计算得到最终的结果.相比于精确乘法器,基于穿孔的近似乘法器将部分积累加步骤减少了2步. 对于本文提出的基于操作数裁剪的近似乘法器,设置k=l=2,则乘法器的输入项更新为: (16) (17) 其中, a′4=or(and(a3,a1),a4) (18) b′4=or(and(b3,b1),b4) (19) 在该近似乘法器中,通过裁剪输入项的部分位,使得对部分积树进行累加时,第1步操作实现对前4行的累加,即前4行部分积树内同一位只包含两个或3个部分积.图4(c)为k和l均设置为2时,8位近似乘法器的部分积累加过程.若k和l设置为1,则该近似乘法器无法实现低功耗部分积累计算法;若k和l设置为3,则会大大降低乘法计算的精度.所以,对于8位近似乘法器,本文将k和l均设置为2. 图4 8位乘法器的部分积累加简化图Fig.4 Accumulation of partial products of(left)the reference 8-bit multiplier,(middle)the perforated-based 8-bit approximate multiplier,(right)the proposed 8-bit approximate multiplier 位乘积运算得到的部分积树一共6行,基于部分积树,该近似乘法器一共需要4步计算得到最终的结果.因此,相比于8位精确乘法器,本文所提出的近似乘法器将部分积累加步骤减少了约42.8%. 同理,为了满足低功耗部分积累加算法要求并保证精度需求,对于10位近似乘法器,将k和l均设置为3,则乘法器的输入项更新为: 英国Romax科技有限公司是世界领先的工程技术咨询公司,总部位于英国诺丁汉,在齿轮箱、轴承和机械传动系统方面拥有丰富的经验和近30年的咨询历史。Romax出色的工程团队和高级虚拟产品开发与仿真软件RomaxDESIGNER家族系列产品,为全球传动汽车、新能源汽车、轨道交通等工业领域的大型设备供应商提供设计、分析及认证支持等服务。 (20) (21) 其中, a′6=or(and(a4,a5),a6) (22) b′6=or(and(b4,b5),b6) (23) 位乘积运算得到的部分积树一共6行,图5为位累加算法的简化过程.由图5可知,基于部分积树,该近似乘法器一共需要4步计算得到最终的结果. 图5 10位近似乘法器的部分积累加简化图Fig.5 Accumulation of partial products of the proposed 10-bit approximate multiplier 而对于10位二进制精确乘法器,一共需要9步部分积累加步骤.因此,近似乘法器将部分积累加步骤减少了约56%. 对于本文所提出的近似乘法器,其操作数裁剪方法和低功耗部分积累加算法是通用的.对于不同位宽的乘法器,通过设置k和l的数值,决定输入项需要裁剪的位,就可实现低功耗的部分积累加算法. 各种近似算法单元差别较大.通常地,在近似乘法器设计完成后,以下几个指标可以用于综合衡量其误差特性: 1)误差率.指近似计算单元错误输出占总输出的比例,可以反应近似计算单元出错的频率; 2)平均误差距离.指近似输出与精确输出的差值,大量输入下的平均效应能更好地反应近似计算单元的误差累积效应,平均误差距离越大,误差累积越严重,对输出质量影响越大.近似计算单元的所有输入具有随机性,可以认为呈现均匀分布,因此对所有输入下的误差距离求均值即可获得平均误差距离; 3)最大误差距离.指近似计算单元在单次计算中可能出现的最大误差,反应最大的误差严重程度.最大误差距离越大,越容易对应用的结果产生严重影响. 在本文中,使用6000对操作数来衡量8位近似乘法器的误差特性,数值大小为0-255的随机正整数,仿真结果如表1所示.除了本文所提出的基于操作数裁剪的近似乘法器以及精确乘法器,与基于穿孔的近似乘法器、DRUM、ESSM等主流输入级近似方法也进行了对比分析. 由表1可知,DRUM是一种精度较高的近似乘法器,平均误差距离和最大误差距离分别为0.84%和6.35%.这是因为它引入了两个最高有效位检测模块,以及两个多路复用器选择进行乘法运算的数据位,动态地对最有效的位进行乘法运算.但是在实际应用中,该乘法器会导致较大的面积与功耗开销. 表1 近似乘法器误差特性仿真结果Table 1 Simulation results of error characteristics of approximate multipliers 基于穿孔的近似乘法器精度非常低,其最大误差距离为100%,并不会随着参数改变而降低.这是因为该近似乘法器处理简单,保留输入项中高位的数据而舍去低位的数据,如果当输入项数值较小或者保留位的值均为0时,就会导致该次结果的误差距离为100%. 与之相比,本文所提出的近似乘法器精度有很大的提升,平均误差距离和最大误差距离分别为3.01%和20.47%.这是因为,本文所提出的基于操作数裁剪的近似乘法器在对输入项裁剪之前,考察了高位全为0的情况.若高位不全为0,则直接裁剪;若高位全为0,则进行移位操作后裁剪,在部分积累加结束后再进行一次移位操作得到最终结果.另外,该近似乘法器在裁剪之后,更新了输入项中部分高位,弥补了数据裁剪对精度的影响. ESSM与基于操作数裁剪的近似乘法器一样,进行了高位考察及移位操作,保证了较高的精确度,其平均误差距离和最大误差距离分别为1.62%和8.75%. 基于Xilinx Vivado 2019.1平台,本节将比较精确乘法器、本文提出的基于操作数裁剪的近似乘法器、基于穿孔的近似乘法器、DRUM、ESSM的性能与资源开销,具体包括查找表(Look-up-tables,LUTs)资源使用量、寄存器资源使用量和片上功耗等. 以8位二进制乘法器为例,图6展示了LUT使用量、功耗开销以及平均误差距离的三维图.为便于在图中展示,将精确乘法器、基于操作数裁剪的近似乘法器、基于穿孔的近似乘法器分别记作PM、TRU-M、PER-M. 从图6中可以看出,一个8位精确乘法器的LUT使用量和片上功耗分别为72和14.7w.PER-M乘法器减少了资源使用和功耗开销,其LUT使用量和片上功耗以及分别为35和9.9w,但是该乘法器误差很大,平均误差距离约为7%. 图6 多种近似乘法器LUT使用量、片上功耗以及平均误差距离的三维图Fig.6 3-D graph of LUT usage,power consumption on chip and average error distance of various approximate multipliers DRUM和ESSM是两种精度较高的乘法器,平均误差距离分别约为0.8%和1.6%,但是资源使用量和功耗较大,LUT使用量分别为93和69,片上功耗分别为14.3w和12.9w. 本文所提出的近似乘法器的LUT使用量、片上功耗以及平均误差距离分别为60、7.8和3%,以3%的精度损失减少了约16.7%的资源使用和46.9%的片上功耗. 基于精确二进制乘法器,本文设计了一种新型近似乘法器.对于8位和10位二进制乘法器,利用操作数裁剪模块和低开销部分积累加算法,可以将部分积累加步骤分别减少约42.8%和56%. 本章对各个乘法器进行了实现,并采用误差率、平均误差距离和最大误差距离衡量了误差特性.结果显示,本文所提出的近似乘法器的精度相比于基于穿孔的近似乘法器有很大的提升,平均误差距离和最大误差距离分别为3.01%和20.47%.由性能评估可知,相比于精确乘法器,该近似乘法器以3.01%的精度损失减少了约16.7%的资源使用和46.9%的片上功耗.3.4 开销分析


4 实验结果与分析
4.1 误差特性仿真
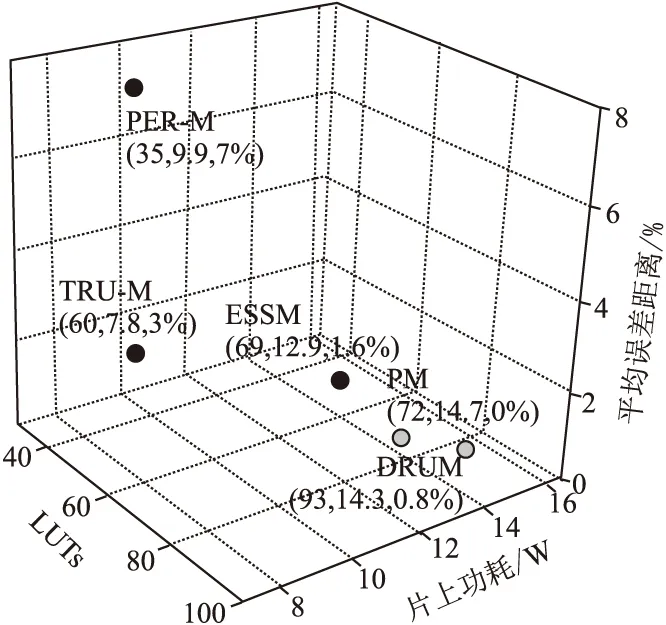
4.2 性能评估
5 结 论

