一类超图的横贯
王 福,石 怡,杜智华
(1石河子大学师范学院,石河子832003;2新疆巴州教育局,库尔勒,841000;3新疆师范大学数学科学学院,乌鲁木齐830054)
一类超图的横贯
王 福1,石 怡2,杜智华3
(1石河子大学师范学院,石河子832003;2新疆巴州教育局,库尔勒,841000;3新疆师范大学数学科学学院,乌鲁木齐830054)
一般超图横贯数τ的上界是不能用匹配数ν的函数来界定的。本文讨论了一类存在这种函数的超图——圈区间超图,得到了此类超图τ与ν之间的关系:τ(H)≤4ν(H),并进一步获得了圈区间超图横贯数的一些性质。
圈区间超图;横贯数;匹配数
横贯是超图中的重要概念,对刻画超图的性质具有重要作用。设H是V上的一个超图,若集合T(⊆V)与H的每条边相交,则称T是H 的一个横贯。H的横贯数τ(H)是指H中最小横贯的基数,简记为τ。H的匹配数ν(H)是指H中两两不相交的最大边数,简记为ν。易知ν≤τ[1]。
一般而言,用ν的函数从上方界定τ是不太可能的。然而,1994年 Qing等[2-3]从理论上给出了超图具有这种性质的一个充分条件。众多学者也一直在研究存在这种函数关系的超图类。Gallai得出了区间超图满足τ=ν;Gyarfas和Lehel[4]证得树的子树超图满足ν=τ;Kaiser[5]用拓扑理论证得:若图G是一条路,超图H的任一边是由G的至多d个连通子图构成的,则有:τ≤(d2-d+1)ν;Alon[6]改进了Kalser的结果,简洁直观地证出相同条件下满足:τ≤2d2ν;Alon[7]又证得:若图G 是一棵树,超图H的任一边是由G的至多d个连通子图构成,则有:τ≤2d2ν;Tar dos[8]结合前人的工作,总结了由树的至多d个连通子图构成超图的v与τ之间关系的三种方法。
本文主要通过横贯数与分数横贯数、匹配数与分数匹配数、横贯数与匹配数之间的关系求得圈区间超图的横贯数与匹配数之间的关系,并进一步获得了此类超图横贯数的一些性质。
1 相关定义与引理
定义1:设V={v1,v2,…,vn}是依次排列在圈上的有限顶点集。超图 H=(E1,E2,…,Em)被称为V 上的圈区间超图,若Ei(i=1,2,…,m)是V 上的一个连续子集,且Ei=V。
定义2[1]:超图H 的分数横贯是V上的实函数τ(ν),满足:
①0≤τ(ν)≤1(∀ν∈V),
定义3[1]:超图H 的分数匹配是一个实函数g(E),满足:
①0≤g(E)≤1(∀E∈H),
Turan引理[2,9]:设G 为阶数为n 的图,若G 中不含r+1个两两不相邻的顶点,则G中至少有-1)条边。
引理1:设超图H有M 条边,若H中不含k+1个两两不相交的边,则H中至少有-1)对相交边。
证明:在超图H 的基础上定义图GH,令V(GH)={xi|若Ei∈H,则xi∈V(GH)};xi与xj之间连一条边当且仅当Ei与Ej相交。可知图GH的阶数为M,且不含k+1个两两不相邻的顶点。
由Tur dn引理得:

从H′中任取一条边E′,不妨设v1与v2为在V上排列在首末两处的顶点,由于与E′相交的边必包含v1与v2之中一个顶点,故v1与v2中有一个顶点至少被条边包含,考虑E′本身,结论成立。
引理3:设m和r是两个正整数,V是圈上的有限顶点集。若R是V上的多重点集,且R中多重点数至多为r m,则存在V的子集S,使得|S|≤m,且V-S每个连通分支包含R中的多重点数少于r个。
证明:对圈上每个顶点v∈V,设其重数为x,显然x≥1。按照下述规则确定子集S:
3)在圈上不断重复这一过程,直至行遍V中所有顶点。设满足条件的顶点集为{,…},则它们构成了子集S。
事实上,如果说明了|S|≤m,就完成了证明。假设|S|=m,恰为最末顶点。仅需验证…+<r即可。由条件可知…+≤r m-r(m-1)-1<r。
引理4[1]:任一超图 H 均满足:v(H)≤v*(H)=τ*(H)≤τ(H)。
2 定理及证明
定理1:设H 是一个圈区间超图,则有:「v*(H)⌉≤4v(H)。
证明:令k=v(H),对V(H)中每一个顶点v,设H 的分数匹配g:H→[0,1]满足(E)≤1,这里g(E)(E∈H)是一个正实数,且H 的分数匹配数v*(H)=(E)。令m是一个正整数,且对每条边E∈H,mg(E)均为整数。设
|H′|=M。
因为H′中不含k+1个两两不相交的边,由引理1可知:在H′中至少有-1)>-4)对相交边。又由引理2知:在V(H)上存在一个顶点v,它被H′中至少条边包含。由于

由此得到:
「v*(H)⌉≤4v(H)。
定理2:设H是一个圈区间超图,则有:τ(H)≤「τ*(H)⌉。
证明:对H的每条边E,设H的分数横贯t:V→[0,1]满足(v)≥1,这里t(v)(v∈V)是一个正实数,且H的分数横贯数τ*(H)=(v)。
令r是一个整数,对每一个v∈V,rt(v)都是整数;又令R是多重集,它由V中每一个顶点的rt(v)个拷贝组成。由于
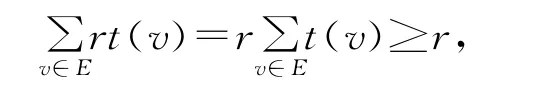
那么H每条边包含R中至少r个多重点。设
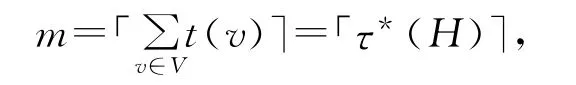
则有R中多重点数为:
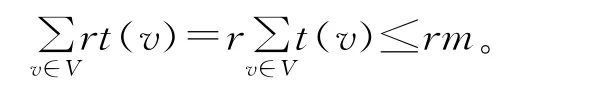
由引理3可知,存在一个V的子集S,使得
|S|≤m=「τ*(H)⌉,
且V-S每个连通分支包含R中的多重点数少于r个,这蕴含着H的每条边都包含S中至少一个顶点。因为若不然,在H 中就存在一条边E,它不包含S中的任何一个顶点,这意味着E含在V-S的一个连通分支中,这个连通分支包含R中多重点数少于r个。但若如此,这与E包含R中至少有r个多重点矛盾。故有:
「τ*(H)⌉≥|S|≥τ(H)。
由定理1和定理2,再结合引理4,可推得重要结论:
定理3:设H是一个圈区间超图,则有:τ(H)≤4v(H)。
3 相关性质
结合引理4和定理2,有下面的推论:
推论1:设H是一个圈区间超图,则有:τ(H)=「τ*(H)⌉。
定义4:设H是一个超图,若H 每条边均含r个顶点,则称H为r一致超图。若H中存在一个被所有边包含的顶点,则称H 是星。H 中边的最小基数称为下秩。

性质2:设H是一个n阶圈区间超图,若H的下秩为s,则有:τ(H)≤⌉。
[1] Berge C.Hypergraphs-Combinational of Finite Sets[M].Amster dam:Nort h-Holland,1989.
[2]帕赫J,阿格瓦尔P K.组合几何[M].丁仁,苏战军,范立平,等译.北京:科学出版社,2008.
[3]Ding,Sey mour P,Winkler P.Bounding the vertex cover nu mber of a hyper graph[J].Co mbinatorica,1994,14:23-34.
[4] Gyarfas A,Lehel J.A Helly-type problem in trees[M]//Erdos.Co mbinatorial Theory and Its Applications.Amsterdam:North-Holland,1970:571-584.
[5]Kaiser T.Transversals of d-intervals[J].Discrete Comput,1997,18:195-203.
[6]Alon N.Piercing d-inter val[J].Discrete Co mput,1998,19:333-334.
[7]Alon N.Covering a hypergraph of subgraphs[J].Discrete Mathematics,2002,257:249-254.
[8] Tardos G.Transversals of d-interval-comparing three approaches[J].Progress in Mathematics,1998,169:234-243.
[9]Bondy J A,Murty S R.Graph Theory With Application[M].London:Macmillan Press,1976.
Transversal of a Hypergraph
WANG Fu,SHI Yi,DU Zhihua
(1 Department of Mathematics,Teachers College,Shihezi University,Shihezi 832003,China;2 Bazhou Education Bureau,Kuerle 841000,China;3 School of Mat hematics-Physics and Information Science,Xinjiang Nor mal University,Urumqi 830054,China)
In general,transversal nu mberτcannot be bounded fro m above by a f unction of matching nu mberνfor hypergraph.Circle-hypergraph is discussed because it satisfies the function,and relevant relationship is revealed bet weenτandνof circle-hyper graph,that is,τ(H)≤4ν(H).It follows that several propositions are obtained aboutτ.
circle-hypergraph;transversal number;matching number
O157.5
A
1007-7383(2011)03-0378-03
2010-01-08
国家自然科学基金项目(60774073)
王福(1981-),男,讲师,从事数学及其应用的研究;e-mail:wf_tea@shzu.edu.cn。

