遗传算法在数值逼近中的应用
张春涛 向瑞银 任友俊
(1.重庆三峡学院数学与计算机科学学院,重庆万州 404100)
(2.曲靖师范学院计算机科学与工程学院,云南曲靖 655011)

遗传算法(Genetic Algorithm,简称GA)是一种更为宏观意义下的仿生算法,它模仿的机制是一切生命与智能的产生与进化过程.它通过模拟达尔文“优胜劣汰、适者生存”的原理激励好的结构;通过模拟孟德尔遗传变异理论在迭代过程中保持己有的结构,同时寻找更好的结构.它是近年来开始得到广泛关注的一种新型非数值优化算法,具有智能性搜索、并行式计算和全局优化等优点,没有传统的建立在梯度计算基础上优化算法的缺点,特别适合于求解目标函数的多极值点问题.[3]
1 遗传算法在最佳一致逼近中的应用

求解函数的最佳一致逼近多项式,关键是确定n次多项式p ( x )的系数,即求p(x) = a0+a1x +…+anxn中的系数a0,a1,…,an.我们可以直接对这些系数编码,进行遗传操作.但当系数较多,即逼近多项式的次数较高,且原函数的值较大,则使得系数的取值范围增大,为了达到理想的精度,则使遗传算法中的个体长度积聚增加,这十分不利于算法的操作.但是我们利用最佳一致逼近的特点:逼近函数与被逼近函数有不同的交点(交点个数与逼近函数的次数有关).因此,我们改为寻找交点,然后用这些交点的插值函数无限地逼近被逼近函数.显然把决策变量改为交点组时的个体长度远远小于决策变量是系数时个体的长度,因为区间是固定的,还可通过缩放区间来减小个体编码长度,并且我们可以用插值函数来进行误差分析.
1.1 算法描述
1.1.1 编码:由问题的描述,我们采用二进制编码方法,即每个系数 ai或每个插值节点 xi(i = 0,1,2,…,n)用固定的k(要经过具体函数在定义区间中的值来决定)位二进制位来表示,因此一个个体要(n+1)*k位二进制位表示,即个体的编码长度l = (n+1)*k.
1.1.2 初始群体的确定.设群体规模N = 100,初始群体中的个体用随机的方法产生.
1.1.3 确定适应值函数 G (x).我们直接计算fabs (f(a) - p(a))的值,其中a是f(x) - p(x)在定义区间中的最大值点,此时 p(x)是由给定的个体解码得到对应的系数或个体解码得到插值节点而定.
1.1.4 选择算子.我们采用比例选择算子,即个体在下一代群体中的个数由该个体的适应值在种群总的适应值中的比例来决定.
1.1.5 交叉算子.我们采用两点交叉算子,交叉概率pc为0.7 < pc< 0.95.
1.1.6 变异算子.我们采用基本位变异算子,变异概率pm为0.001 < pm< 0.1.
1.1.7 终止条件.取最大迭代次数T < 100或插值误差充分小.
1.2 仿真实验
例1.求函数f(x)=ex在 [-1,1] 上的二次多项式逼近.
显然最佳逼近多项式 p(x) 具有如下形式:p(x) = a0+a1x+a2x2,我们分别用雷米兹方法、遗传算法和切比雪夫节点插值法对其求解,结果如表1所示:

表1 ex的二次最佳一致逼近
例2.求函数f(x) = ex在[-1,1]上的三次多项式逼近 p(x) = a0+a1x+a2x2+a3x3.
此时,在用遗传算法求解时,不直接求其系数,改为求交点,然后用拉格朗日进行节点插值.则

我们分别用雷米兹方法、遗传算法和切比雪夫节点插值法对其求解,结果如表2所示:

表2 ex的三次最佳一致逼近
例3.求函数f(x) = e(x/2)*sin(x)*cos(x/5)在[-1,1]上的三次多项式逼近.
此时的逼近函数 p (x) 有如下形式:
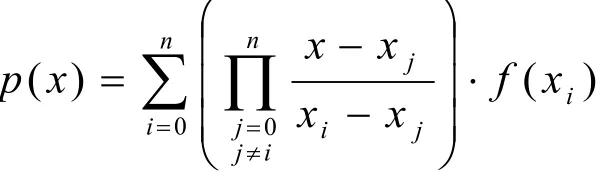
仍采用上面的三种算法进行求解,结果见表3:
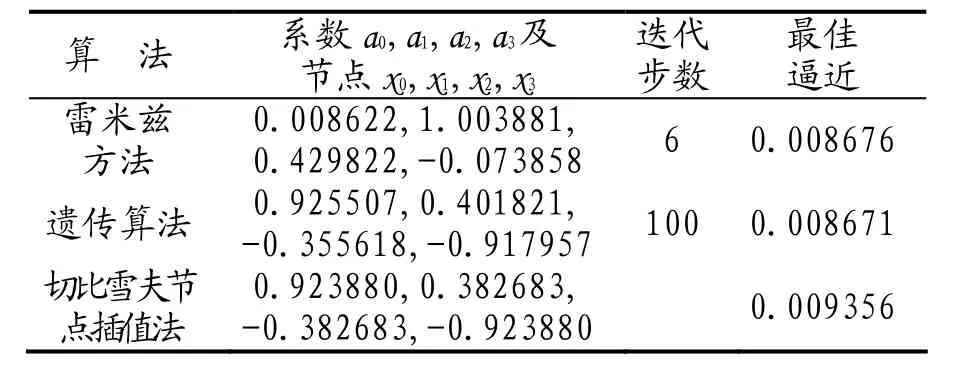
表3 f(x)的三次多项式逼近
我们画出逼近函数和被逼近函数的图形,如图1所示:(其中*是f(x)的图形,虚线是p(x)的图形)
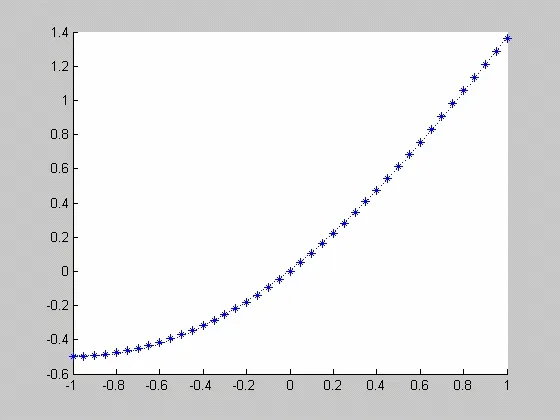
图1 函数和逼近多项式的图象
从上面的三个示例可以看出用雷米兹方法求解函数的最佳一致逼近多项式有很快的收敛速度和很高的精度,但对初始点组有依赖性,计算较复杂,而用遗传算法求解收敛也较快,精度也较高,而且当逼近函数的阶较高时,逼近函数能很好地表示被逼近函数.
2 遗传算法在最佳平方逼近中的应用
前面介绍的最佳一致逼近考虑的是整个区间上绝对误差的最大值,计算量一般较大.同时,对于那些仅有个别小区段上有较大误差的函数,反而不能很好地反映其真实情况,因为它过于迁就原函数的某一峰值,造成逼近函数整体上偏离被逼近函数(原函数).
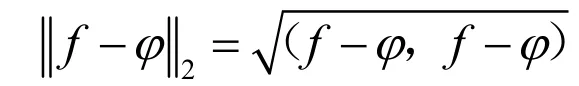
求解最佳平方逼近函数的传统算法很多,下面我们用遗传算法来求解.
2.1 算法描述
2.2 仿真实验
例4.求f (x) = ex,x∈[0,1]的最佳二次平方逼近多项式.计算结果如表4.

表4 平方逼近和一乘逼近
3 遗传算法在最小一乘逼近中的应用
当原函数的峰值较多且较突时,由最佳平方逼近的计算可知,它放大了逼近函数和被逼近函数的误差,使逼近函数迁就被逼近函数的某些峰值而偏离被逼近函数.下面我们用另一近似标准,即1-范数的最小一乘逼近.
定义2.f (x)∈C [a, b],则f(x)的1-范数定义为:

在C [a,b]中定义了1-范数后,C [a,b]就成为一种线性赋范空间.最小一乘逼近问题可描述为:

由于1-范数的不可微性,使得求解最小一乘逼近函数较难,因为传统的优化算法一般要基于梯度的信息.遗传算法不需要梯度信息,只要目标函数可计算就行,因此我们可以用遗传算法来计算最小一乘逼近函数.
3.1 算法描述
3.2 仿真实验
例5.求f(x) = ex,x∈[0,1]的最小一乘逼近二次多项式.计算结果如表4所示.
例6.求f(x) = sin(x) + 6xex,χ∈[0,1]的最小一乘和最佳平方逼近二次多项式.结果如表5所示.

表5 最小一乘和最佳平方逼近多项式
从表4和表5可以看出使用遗传算法能较方便的求解出函数的最佳平方和最小一乘逼近多项式。
4 结论
本文讨论了遗传算法在最佳一致逼近、最佳平方逼近和最小一乘逼近中的应用,根据遗传算法基本与问题的复杂程度无关和不需目标函数可导等一些辅助信息的特性,找到了求解1-范数的最小一乘逼近问题的有效算法.我们用遗传算法求解了基于三种范数的逼近函数,效果较明显,最重要的是可以将该求解方法推广到基于任何范数的逼近函数和任意范数的数据拟合上去,当然操作策略可以改进,从而不必为每种范数逼近问题设计各自不相关的算法.
[1]马振华.现代应用数学手册 计算方法分册[M].北京:北京出版社,1990.
[2]杨大地,涂光裕.数值分析[M].重庆:重庆大学出版社,1998.
[3]周明,孙树栋.遗传算法原理及应用[M].北京:国防工业出版社,1999.
[4]张春涛.遗传算法在信息论中的应用[J].重庆三峡学院学报,2008(3).

