基于Rough集的集成离散化算法

刘 静 何贤芳

（1.重庆三峡学院实验中心，重庆万州 404100）

（2.重庆信息学院，重庆万州 404100）

波兰逻辑学家Z. Pawlak教授于1982年提出粗糙集理论，[1][2][3]它是一种软计算工具，能有效地分析和处理不精确、不一致、不完整等各种不完备信息，并能从中揭示潜在的规律.近年来粗糙集理论广泛应用于机器学习、数据挖掘等多个领域.[4]

经典的Rough集理论处理的数据类型主要针对的是离散型，而现实世界的数据大多是连续型，因此，离散化处理对于基于Rough理论的知识获取方法至关重要.近年来，国内外很多学者已经对离散化方法进行了相关研究，并提出了多种算法，如文[4]介绍了等距离划分的离散化算法和等频率划分的离散化算法，文[5]提出了一种结合多项式超平面与支持向量机的离散化算法，文[6]提出了基于云理论的离散化算法，文[7]提出了基于层次聚类的离散化算法，文[8]给出了基于分割区间合并的离散化算法，这类算法有一个共同特征就是不考虑决策表离散化前后的相容性问题，虽然离散化处理速度较快，离散化后却可能会导致决策表中的对象产生新的不相容.另一类算法则充分考虑离散化前后决策表的相容性.如文[9，10]提出了基于断点重要性的离散化算法和贪心算法，这是两种被广大研究人员认可的识别率较高的离散化算法，文[11]提出了基于信息熵的离散化算法.此类算法虽考虑了决策表的相容性，但算法的计算复杂性较高，当决策表的候选断点数时较大时，运算速度较慢，处理大数据集的性能有待提高.文[12]提出了基于属性重要性的离散化算法，该算法考虑了决策表的相容性且离散化速度较快，但离散化后断点较多，识别率较低.因而，研究新的离散化算法是非常有必要的.

本文分析了基于断点重要性和基于属性重要性两种粗糙集离散化算法，根据这两种算法的特点提出了基于Rough集的集成离散化算法，实现了整个决策表的离散化.实验结果表明：文中提出的离散化算法在识别率上和Skowron教授提出的贪心算法相当，且能快速处理大数据集.

1 Rough集的基本概念

定义 1（决策表[4]）：一个决策表 S＝＜U,A=C∪D,V, f＞,其中，U是对象的集合，也称为论域，A=C∪D是属性集合，C和D分别称为条件属性集和决策属性集，D≠φ，V是属性值的集合， f: U× A→ V 是一个信息函数，它指定了U中每个对象x的属性值.

定义 2（不分明关系[4]）：给定决策表 S＝＜U,A=C∪D,V, f＞,对于每个属性子集B⊆A，定义一个不分明关系IND(B)，即

显然，不分明关系是一种等价关系.

定义3（上、下近似集[4]）：给定决策表S＝＜U, A=C∪D,V, f＞,对于每个子集X⊆U和不分明关系IND(B)，X的上、下近似集分别可以由B的基本集定义如下：

定义4（条件分类和决策分类[4]）：给定决策表S＝＜U, A=C∪D,V, f＞，C和D分别为决策表的条件属性集和决策属性集，U|IND(C)和U|IND(D)分别为论域U在属性集C和D上形成的划分，条件分类定义为：Ei∈U|IND(C) (i=1,…,m, m为条件分类的个数)；决策分类定义为：Xj∈U|IND(D) (j=1,…,n, n为决策分类的个数).

2 Rough集离散化算法分析

基于Rough集的离散化算法要求离散化前后应保持决策表数据相容性.很多学者都对此进行了深入的研究，并提出了很多的离散化方法，根据断点选择的过程，又可以把离散化算法分为“逐步添加断点”和“逐步删除断点”的离散化算法.文[10]中的基于断点重要性的离散化算法属于“逐步添加断点”的离散化算法，该算法非常强调候选断点之间的相互影响，在实验中都能取得比较好的效果，不足之处是该算法在对候选断点的选择问题上，采取了“每选择一个断点，都需要计算剩余所有候选断点的重要性值”的策略，当属性值为浮点且数据量较大时，候选断点的数目会接近决策表中的对象数，因而直接导致了算法的效率不高；文[12]中的基于属性重要的离散化算法属于“逐步删除断点”的离散化算法，该算法按照属性重要性对候选断点依次进行删除判定处理，弱化了候选断点之间的相互影响，运行速度较快，但是该算法对属性进行了排序，依次对属性上的断点进行“删除判断处理”，这种处理方式会导致最终得到的断点数目多，从而识别率不高.

2.1 断点重要性及规律分析

文献[10]中给出了一种计算断点重要性值的方法.该算法用断点能区分的实例个数来衡量断点的重要性.将能够被断点区分开的实例对的个数定义为其中：为属性a的第i个断点，为属性a的断点总数，集合X基 (X⊆U)是由断点可以分开的实例的集合，U为属性全集.

决策属性值为 j( j= 1,...,r,r为决策的种类数)的实例中，属于X且属性a的值小于断点值的实例的个数记为

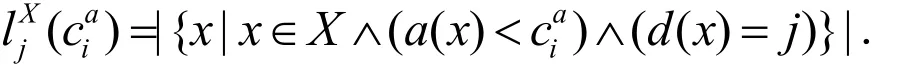
所以有：

该算法每次在所有候选断点集中选取重要性最高的断点，因而得到的断点数目较为合理.但也正是由于它每一次选择都要重新遍历所有候选断点集，当数据集断点规模较大时，执行效率不高.

2.2 基于属性重要性的算法

基于属性重要性的算法将知识定义为对对象进行分类的能力，该算法通过对分类能力的影响程度来评价属性的重要性.为了衡量属性的重要性程度，可从决策表中删除这一属性，再考察决策表的分类会产生的变化.如果去掉该属性会相应地改变分类，则说明该属性重要性高；反之，说明该属性的重要性低.该算法首先求出所有的候选断点，然后求出条件属性的重要性，对条件属性按照属性重要性由小到大对断点进行处理，如果相邻断点合后，决策表不引入冲突，则该断点为冗余断点，否则加入断点集，从而将连续值属性离散化.这样可以使属性重要性较小的属性的断点被淘汰的可能性更大，避免了从属性重要性较大的属性中去掉过多的断点.

此算法的优点是不改变信息系统的不可分辨关系，还可以删除冗余的属性，从而减少了数据集的空间维数且运行速度较快.但仅考虑单个属性的重要性，没有考虑各条件属性之间的相互关系，可能会导致结果断点集产生冗余，得到断点过多，因而识别率不高.

2.3 基于Rough集的集成离散化算法

根据以上两种算法的特点，我们考虑：如果先用基于属性重要性的算法对决策表进行离散化，降低候选断点的数目，然后在所有属性上用基于断点重要性的算法对候选断点区间进行选取，可能会又好又快地实现决策表的离散化.故此，提出了基于Rough集的集成离散化算法.

算法1 基于Rough集的集成离散化算法

Input：决策表 S =＜ U,A =C ∪ D,V,f ＞

Output：决策表S的断点集 CUTlast和离散化后的决策表S

Step1：根据条件属性的重要性由小到大对条件属性进行排序；在属性重要性相同的情况下，按条件属性断点个数由多到少对条件属性进行排序；

Step2：对每个属性上的断点进行如下过程：将每个断点相邻的两个属性值的较小值改为较大值，如果决策表不引入冲突，则去掉该断点；否则，把修改过的属性值还原.由此生成新的候选断点集CUTfirst；

Step3：令L表示实例能被断点集 CUTlast所划分成的等价类的集合， CUTlast=Ø,L ={U};

Step4： 对 每 一 个 c∈CUTfirst， 计 算WCUTlast(c)；

Step5：选择 WCUTlast(c)最大的断点cmax添加到CUTlast中，令

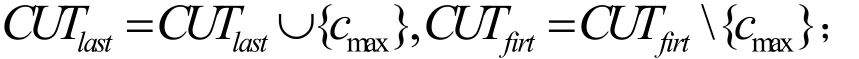
Step6：对所有的X∈L，如果cmax把等价类X分成X1和X2，那么，从L中去掉X，把等价类X1和X2加到L中.

Step7：如果L中个等价类中的实例都具有相同的决策则算法结束，否则转到Step3.

Step8：使用断点集 CUTlast离散化决策表S，得到新决策表S1， S=S1；

Step9：RETURN CUTlast和离散化后的新决策表S.

设条件属性平均取值个数为w，即平均断点个数为w×|C|.Step～Step2是一个典型的基于属性重要性算法，其时间复杂度为：

Step3～Step7是一个典型的基于断点重要性算法，其时间复杂度为：

所以算法1的时间复杂度为：

（这里的k表示经第一次离散化后条件属性上平均断点个数）.空间复杂度为：

3 实验结果

为了验证本文提出算法的运行效率和离散化效果，从UCI数据库中选取8组数据集进行测试，表1是每个数据集的记录数和条件属性个数.对于每组数据集，随机抽取一半作为训练集，另一半作为测试集，随机抽取5次取平均值作为最终的测试结果.每个数据集均采用同样的方法进行规则提取.相关实验数据如表1、表2和表3所示.

表1 仿真试验数据集

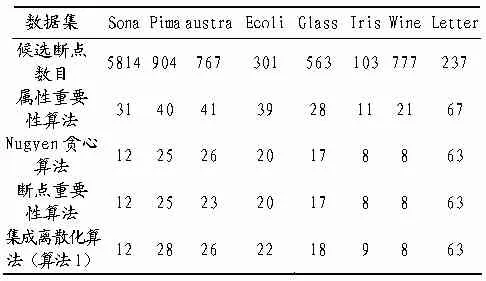
表2 离散化后得到的断点个数

表3 离散化算法运行时间和正确识别率

从表2可以看出，使用基于属性重要性的算法进行初次离散化后，各数据集的候选断点数目大规模下降.

从表3可以看出，算法1的正确识别率与贪心算法、基于断点重要性的离散化算法基本相当，但是运行速度更快，处理的数据量更大.从算法1的时间复杂度分析，算法1与基于断点重要性的离散化算法在时间复杂度是相当的，但经过基于属性重要性的算法初次离散化处理后，候选点急剧下降，因此，虽然算法1的时间复杂度与基于断点重要性算法相同，但运行速度要高于贪心算法和基于断点重要性的离散化算法.

4 结束语

在基于Rough集的知识获取过程中，离散化是首要解决的问题.现有的很多离散化算法没有结合Rough集的特性，在很大程度上阻碍了Rough集实际应用.文中分别分析了基于断点重要性的算法和基于属性重要性的算法，确定了“首先用基于属性重要性的算法进行初次离散化，然后在所有条件属性集上进行断点选择”的离散化思路，提出了基于Rough集的集成离散化算法.实验结果表明，通过两种离散化算法的集成，能有效的选中重要的候选断点，大大降低了候选断点的数目，提高了算法的运算效率，同时，也保持了与已有算法可比的识别率.

[1]Pawlak Z. Rough Set[J]. International Journal Of Computer and Information Sciences, 1982, 11: 341-356.

[2]Pawlak Z., Grzymala-Busse J., Slowinski R., Ziarko W. Rough sets[J]. Communications of the ACM, 1995, 38(11): 89-95.

[3]Pawlak Z. Vagueness-a rough set view[A]. In: Mycielski J., Rozenberg G., Salomaa A., eds. Structures in Logic and Computer Science: A selection of Essays in Honor of Andrzej Ehrenfeucht[C], Berlin: Springer-Verlag, 1997: 106-117.

[4]王国胤.Rough集理论与知识获取[M].西安:西安交通大学出版社，2001.

[5]何亚群，胡寿松.粗糙集中连续属性离散化的一种新方法[J].南京航空航天大学学报，2005，35（3）: 213-215.

[6]李兴生.一种基于云模型的连续属性离散化方法[J].模式识别与人工智能，2006，16（3）:33-38.

[7]Li M X, Wu C D, Han Z H, Yue Y. A hierarchical clustering method for attribute discretization in rough set theory [A]. In: Proceedings of 3th International Conference on Machining Learning and Cybemetics[C], Shanghai, 2004: 3650-3654.

[8]Su C T, Hsu J H. An extended Chi2 algorithm for discretization of real value attributes [J]. IEEE Transaction on Knowledge and Data Engineering, 2005, 17（3）: 437-441.

[9]Skowron A, Rauszer C. The discernibility functions matrics and functions in information systems [A], in: Intelligent Decision Support-Hand-book of Applications and Advances of the Rough Sets Theory [C], edited by Slowinski A, Dordrecht, Kluwer Academic Publisher, 1992: 331-362

[10]Nguyen H S, Nguyen S H. Some efficient algorithms for rough set methods [A], in: Proceedings of the Sixth International Conference, Information Processing and Management of Uncertainty in Knowledge-Based Systems (IPMU"96) [C], Granada, Spain, 1996: 1451-1456.

[11]谢宏，程浩忠，牛东晓.基于信息熵的粗糙集连续属性离散化算法[J].计算机学报，2005，28（9）: 1570-1574.

[12]候利娟，王国胤，吴渝.粗糙集理论中的离散化问题[J].计算机科学，2000，27（12）:89-94.