不相容决策表求核方法
陈凤娟
(辽宁对外经济贸易学院 信息技术系,辽宁 大连116052)
0 引 言
属性约简 (知识约简)是粗糙集理论中的一个主要研究方向。核属性是决策表中最重要的特征集合,它包含在所有属性约简之中,可以作为属性约简的基础,因此很多属性约简算法都从核属性出发,在核属性之上通过一定的方法选取属性增加到核中,从而得到约简集合[1]。
HU XIAOHUA等学者在文献 [2]中给出的利用改进差别矩阵求核的方法是一个很有效的方法,但是有学者已经证明该方法不适用于不相容决策表求核[3-4]。目前,在不相容决策表的求核问题上,主要的方法有使用代数定义[11,13-14]、HU 差别矩 阵[9-10,12,15]、 使 用 信 息 熵 定 义[5,7-8]和改进的 HU差别矩阵[3-4,6]等方法,但这些方法并没有完全解决不相容决策表的求核问题。本文深入分析不相容决策表的性质,把不相容决策表中的核属性分为相容核与不相容核两部分,以文献 [3]和文献 [5]中使用的3个不相容决策表为例,分析这3个不相容决策表的相容核与不相容核,比较现有的求核方法,发现这些方法不能够得到正确的相容核与不相容核,通过改进HU差别矩阵得到两个新的差别矩阵,利用这两个新的矩阵计算出不相容决策表的相容核与不相容核。
1 基本概念
代数观中的正域、属性必要性及核属性的相关概念如下[1]:
定义1 设U为一个论域,P,Q为定义在U上的两个等价关系族,Q的P正域记作POSP(Q),定义为POSP。
定义2 设U为一个论域,P,Q为定义在U上的两个等价关系族,对于P中的关系r,若有POSIND (P)(IND (Q))=POSIND (P- {r})(IND (Q)成立,则称r∈P为P中Q不必要的;否则称r为P中Q必要的。
定义3 设U为一个论域,P,Q为定义在U上的两个等价关系族,P中所有Q必要的原始关系族,称为P的Q核,记为COREQ (P)。
核属性是必要属性的集合。
从上面的定义可知,当去掉某个属性会导致正域发生变化时,则该属性是核属性。
在不相容决策表中,论域中的元素可以通过计算正域的方法,分成不包含冲突信息的相容元素和包含冲突信息的不相容元素两部分。使用代数定义求核的方法通过判断正域是否变化来得到核属性,由于不相容元素的划分块之间的合并对正域完全没有影响,因此,这种方法能忽略掉不相容决策表中的不相容元素之间的变化规律,把去掉后会导致正域发生变化的属性称为核属性,本文称这种核属性为相容核属性。
有两种情况会导致一个不相容决策表的正域发生变化——一个相容元素的划分块和一个不相容元素的划分块发生合并;一个相容元素的划分块和另一个相容元素的划分块发生合并。多于两个的划分块的合并都可以分解成上面两种情况。由于这两种情况会影响正域,因此定义不相容决策表的相容核如下。
定义4 在不相容决策表中,若去掉某一个条件属性,会使包含相容元素的划分块与其它划分块发生合并,导致正域发生变化,则该属性属于相容部分的核属性,简称相容核。
从决策表的正域的变化中不能看到不相容信息是否发生了变化,由于负域与正域完全对应,因此也不能用负域来作为衡量不相容部分是否变化的基准。
由于正域发生变化的本质就是包含相容元素的划分块与别的划分块发生了合并,因此可以用不相容信息的划分块之间的合并作为衡量不相容部分是否发生变化的标准。也就是说如果去掉某个属性会导致不相容部分信息的划分块发生合并,那么这个属性对不相容部分就是必要的属性,就是不相容部分的核属性。为了区别于相容部分的核,称这部分核属性为不相容核。这种属性的存在能保证不相容决策表中不相容部分的划分块保持不变。根据这类属性与决策表的不相容部分信息的变化之间存在的内在联系,给出如下的不相容决策表的不相容核的定义。
定义5 在不相容决策表中,若去掉某一个条件属性,会使包含不相容元素的划分块之间发生合并,则该属性属于不相容部分的核属性,简称不相容核。
对于一个不相容决策表,完整的核属性包含两部分,即相容核与不相容核。相容核部分能考察相容部分的变化,而不相容核能考察不相容部分的变化。一个核属性只能是相容核与不相容核中的一种,不可能二者兼为。
2 现有求核方法存在的问题
在文献 [3]中,叶东毅教授分析了HU差别矩阵运用于不相容决策表中求核时产生的错误,并改进HU差别矩阵,得到与代数定义相同的结果。叶的方法通过改进HU矩阵,把不相容信息对HU矩阵的影响去掉,只计算与相容部分信息相关的属性。类似的改进矩阵的方法还有很多,如杨明的改进矩阵等[4,6],这些方法虽然得到不同形式的差别矩阵,但是它们的思想是完全一致的,都是把不相容决策表中影响计算结果的冲突信息忽略掉。这类改进HU矩阵的方法计算结果与代数定义方法完全相容,可以与代数定义方法归为一类。
在文献 [5]中,王国胤教授使用条件信息熵的方法计算不相容决策表的核,由于条件信息熵是由不相容信息产生的,因此计算条件信息熵的方法能考察到不相容部分的变化,但是由于条件信息熵是由比率得到的,因此当某些不相容部分的划分块发生了合并,而其比率不发生变化的情况,就会被条件信息熵方法忽略掉,导致该方法不能判断所有的不相容划分块发生合并的情况。
下面针对文献 [3]和文献 [5]中用到的3个不相容决策表,分别分析这些决策表中相容部分划分块和不相容部分划分块的变化,从而说明现有的求核方法存在的问题,如表1~表3所示。

表1 不相容决策表1
决策表1的划分如下:
U/IND ({C1,C2,C3})= {{x1,x2}, {x3,x4},{x5}};
U/IND (D)= {{x1,x3,x5},{x2,x4}};
正域POSC(D)= {x5}。
去掉属性C1,有 U/IND ({C2,C3})= {{x1,x2,x3,x4},{x5}};
去掉属性C2,有 U/IND ({C1,C3})= {{x1,x2,x5},{x3,x4}};
去掉属性C3,有 U/IND ({C1,C2})= {{x1,x2},{x3,x4},{x5}};
从上面的计算可知:
(1)决策表1中相容部分为 {x5},相容部分的划分为{{x5}},存在不相容信息的部分为 {x1,x2,x3,x4},不相容部分的划分为 {{x1,x2},{x3,x4}};
(2)去掉属性C1,相容部分的划分没有发生变化,而不相容部分的划分发生了变化,即不相容部分的划分块{x1,x2}和 {x3,x4}合并成了一个划分块 {x1,x2,x3,x4},因此,C1属于不相容核。
(3)去掉属性C2,使相容部分的划分块 {x5}和不相容部分的划分块 {x1,x2}合并成了一个划分块 {x1,x2,x5},导致正域POSC(D)发生变化,因此,C2属于相容核。
(4)去掉属性C3,对相容部分的划分没有影响,对不相容部分的划分也没有影响,因此,C3不属于任何核。
由以上分析可得,决策表1的核属性集为 {C1,C2},其中,相容核为 {C2},不相容核为 {C1}。代数方法求得的核为相容核 {C2};改进的差别矩阵 (如文献 [3-4]所示)中求得的也是相容核 {C2};信息熵的方法求得的核也是相容核 {C2};HU矩阵的方法求得的核是 {C1,C2},是所有的核。

表2 不相容决策表2
决策表2的划分如下:
U/IND ({C1,C2,C3})= {{x1},{x2,x3},{x4}};
U/IND (D)= {{x1,x3},{x2,x4}};
正域POSC(D)= {x1,x4}。
去掉属性C1,有U/IND ({C2,C3})= {{x1,x2,x3},{x4}};
去掉属性C2,有 U/IND ({C1,C3})= {{x1,x4},{x2,x3}};
去掉属性C3,有 U/IND ({C1,C2})= {{x1},{x2,x3},{x4}}。
从上面的计算可知:
(1)决策表2中相容部分为 {x1,x4},相容部分的划分为 {{x1},{x4}},存在不相容信息的部分为 {x2,x3},不相容部分的划分为 {{x2,x3}};
(2)去掉属性C1,使相容部分的划分块 {x1}和不相容部分的划分块 {x2,x3}合并成了一个划分块 {x1,x2,x3},导致正域POSC(D)发生变化,因此,C1属于相容核。
(3)去掉属性C2,使相容部分的划分块 {x1}和 {x4}合并成了一个划分块 {x1,x4},导致正域POSC(D)发生变化,因此,C2属于相容核。
(4)去掉属性C3,相容部分的划分和不相容部分的划分都没有发生变化,因此,C3不属于任何核。
由以上分析可得,决策表2的核属性集为 {C1,C2},其中,相容核为 {C1,C2},不相容核为Φ。代数方法、改进的差别矩阵方法、信息熵的方法和HU矩阵的方法求得的核都是 {C1,C2}。

表3 不相容决策表3
决策表3的划分:
U/IND ({C1,C2,C3})= {{x1,x2,x3}, {x4,x5},{x6}};
U/IND (D)= {{x1,x4,x6},{x2,x5},{x3}};
正域POSC(D)= {x6}。
去掉属性C1,有 U/IND ({C2,C3})= {{x1,x2,x3,x4,x5},{x6}};
去掉属性C2,有 U/IND ({C1,C3})= {{x1,x2,x3,x6},{x4,x5}};
去掉属性C3,有 U/IND ({C1,C2})= {{x1,x2,x3},{x4,x5},{x6}}。
从上面的计算可知:
(1)决策表3中相容部分为 {x6},相容部分的划分为{{x6}},存在不相容信息的部分为 {x1,x2,x3,x4,x5},不相容部分的划分为 {{x1,x2,x3},{x4,x5}};
(2)去掉属性C1,使不相容部分的划分块 {x1,x2,x3}和 {x4,x5}合并成了一个划分块 {x1,x2,x3,x4,x5},因此,C1属于不相容核。
(3)去掉属性C2,使相容部分的划分块 {x6}和不相容部分的划分块 {x1,x2,x3}合并成了一个划分块 {x1,x2,x3,x6},导致正域POSC(D)发生变化,因此,C2属于相容核。
(4)去掉属性C3,相容部分的划分和不相容部分的划分都没有发生变化,因此,C3不属于任何核。
由以上分析可得,决策表3的核属性集为 {C1,C2},其中,相容核为 {C2},不相容核为 {C1}。代数方法和改进的差别矩阵的方法求得的核是相容核 {C2},信息熵的方法和HU矩阵的方法求得的核是所有核 {C1,C2}。
对于上面的表1、表2和表3,代数方法和改进的差别矩阵方法完全等价,它们只能求得不相容决策表的相容核;信息熵方法有时得到的是相容核,有时得到的是全部核属性;HU矩阵方法能计算出不相容决策表的全部核属性。
HU矩阵方法虽然得到了全部的核属性集合,但是该矩阵把这两种核属性混合在一起,使人很难分辨出哪个是相容核,哪个是不相容核,这种现象使得许多学者认为HU矩阵不适用于不相容决策表。
下面通过对HU差别矩阵进行修改,使HU矩阵中的相容核与不相容核分开,从而得到不相容决策表的所有的核属性集合。
3 改进的差别矩阵
HU差别矩阵定义如下:
定义6 对于信息系统S= (U,A,V,f),A=C∪D,C∩D=Φ,C和D分别是条件属性和决策属性。S的差别矩阵M是一个n*n对称矩阵,a(x)是记录x在属性a上的值,mij表示差别矩阵中第i行,第j列的元素,因此差别矩阵定义为

文献中给出如下结论:当且仅当某个mij为单个属性时,该属性属于核CORE(C)。
根据前面给出的相容核与不相容核的计算过程及方法,修改HU矩阵为下面两个新的矩阵,这两个矩阵分别计算不相容决策表的相容核与不相容核。
定义7 对于信息系统S= (U,A,V,f),A=C∪D,C∩D=Φ,C和D分别是条件属性和决策属性。S的差别矩阵MS1和MS2都是n*n的对称矩阵,a(x)是记录x在属性a上的值,mij和m′ij分别表示差别矩阵MS1和MS2中第i行,第j列的元素,这两个差别矩阵分别定义为
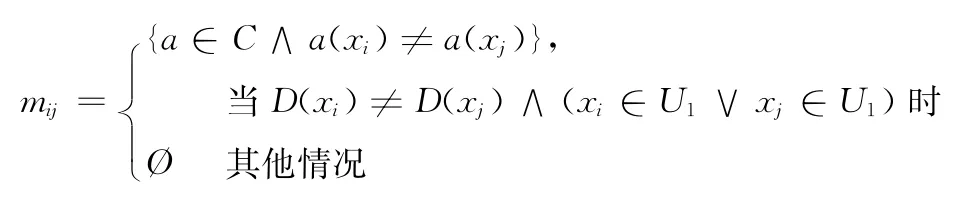
其中U1=POSC(D)。当mij为单个属性时,该属性是相容核属性。这个结果与代数观的核属性定义方法计算的核属性等价

其中U2=U-POSC(D)。当m′ij为单个属性时,该属性是不相容核属性,删除该属性将导致大于等于两个不相容部分块发生合并。它的存在保证了不相容部分的分类与原始决策表的不相容部分的分类一致。
下面使用改进的两个差别矩阵,计算以上3个不相容决策表的相容核与不相容核,由矩阵的对称性,可以只计算这些矩阵的下三角矩阵。
决策表1的新的差别矩阵MS1和MS2如表4和表5所示。

表4 决策表1的差别矩阵MS1
由于C2是矩阵MS1中的单个属性,因此,C2是相容核。

表5 决策表1的差别矩阵MS2
由于C1是矩阵MS2中的单个属性,因此,C1是不相容核。
决策表2的新的差别矩阵MS1和MS2如表6和表7所示。
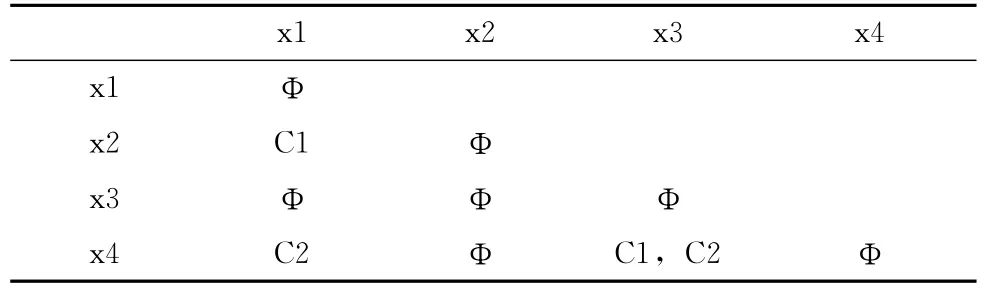
表6 决策表2的差别矩阵MS1
由于C1,C2都是矩阵MS1中的单个属性,因此,C1,C2都是相容核。
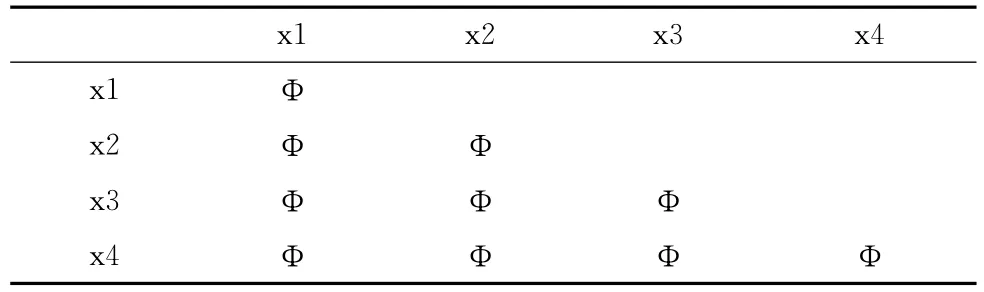
表7 决策表2的差别矩阵MS2
由于矩阵MS2中的没有单个属性,因此,该决策表的不相容核为Φ。
决策表3的新的差别矩阵MS1和MS2如表8和表9所示。

表8 决策表3的差别矩阵MS1
由于C2是矩阵 MS1中的单个属性,因此,C2是相容核。
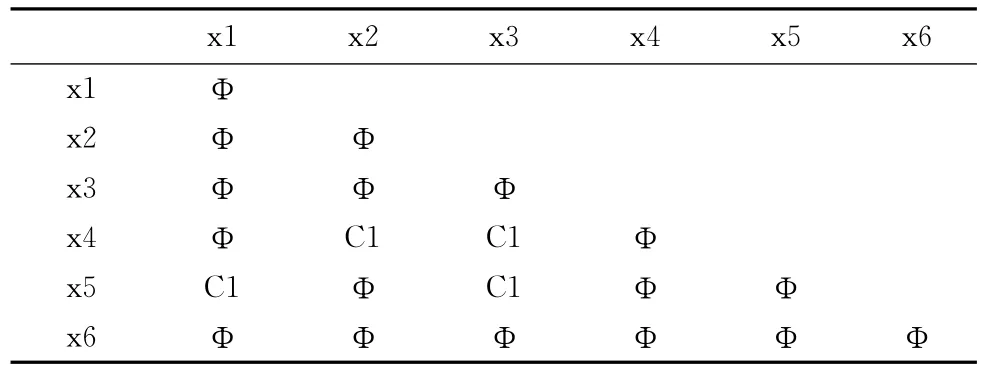
表9 决策表3的差别矩阵MS2
由于C1是矩阵MS2中的单个属性,因此,C1是不相容核。
改进的差别矩阵MS1处理所有相容元素参与的比较,所以该矩阵中的单个元素是相容部分的核属性,即相容核;而改进的差别矩阵MS2处理不相容元素之间的比较,所以该矩阵中的单个元素是不相容部分的核属性,即不相容核。
4 结束语
对于不相容决策表的核属性的计算问题,一直有很多种方法。代数定义的方法能忽略掉不相容决策表中的不相容部分的信息,很多改进的差别矩阵方法也都以得到与代数方法相同的结果为目标。本文在深入研究不相容决策表的特性后,把不相容决策表的核属性分为相容核与不相容核两部分。通过改进HU差别矩阵得到两个新的差别矩阵,这两个差别矩阵能分别计算出不相容决策表的相容核与不相容核。
[1]WANG Guo-yin.Rough set theory and knowledge acquisition[M].Xi’an:Xi’an Jiaotong University Press,2001 (in Chinese).[王国胤.Rough集理论与知识获取 [M].西安:西安交通大学出版社,2001.]
[2]HU X H,Cercone N.Learning in relational databases:A rough set approach [J].Computation Intelligence,1995,11(2):323-337.
[3]YE D Y,CHEN Z J.A new discernibility matrix and the computation of a core[J].Acta Electronica Sinica,2002,30 (7):1086-1088(in Chinese).[叶东毅,陈昭炯.一个新的差别矩阵及其求核方法 [J].电子机学报,2002,30 (7):1086-1088]
[4]YANG Ming,SUN Zhi-hui.Improvement of discernibility matrix and the computation of a core [J].Journal of Fudan University (Nature Science),2004,43 (5):865-868 (in Chinese).[杨明,孙志挥.改进的差别矩阵及其求核方法 [J].复旦大学学报 (自然科学版),2004,43 (5):865-868.]
[5]WANG Guo-yin.Calculation methods for core attribute of decision table[J].Chinese Journal of Computes,2003,26 (5):611-615(in Chinese). [王国胤.决策表核属性的计算方法[J].计算机学报,2003,26 (5):611-615.]
[6]YANG Ming,YANG Ping.Discernibility matrix enriching and computation for attributes reduction [J].Computer Science,2006,33 (9):181-183 (in Chinese). [杨明,杨萍.差别矩阵浓缩及其属性约简求解方法 [J].计算机科学,2006,33(9):181-183.]
[7]WANG G Y,YU Hong,YANG D C.Decision table reduction based on conditional information entropy [J].Chinese Journal of Computers,2002,25 (7):759-766 (in Chinese). [王国胤,于洪,杨大春.基于条件信息熵的决策表约简 [J].计算机学报,2002,25 (7):759-766.]
[8]XU Zhang-yan,YANG Bing-ru,GUO Yan-ping,et al.Quick algorithm for computing core based on information entropy [J].Journal of Chinese Computer Systems,2007,28 (2):279-282 (in Chinese).[徐章艳,杨炳儒,郭燕萍,等.基于信息熵的快速求核算法 [J].小型微型计算机系统,2007,28 (2):279-282.]
[9]YE Dong-yi,CHEN Zhao-jiong.Improved method for computing all attribute reducts of an inconsistent decision table [J].Mini-Micro Systems,2006,27 (10):1909-1913 (in Chinese). [叶东毅,陈昭炯.不相容决策表全部属性约简计算的一个改进方法[J].小型微型计算机系统,2006,27 (10):1909-1913.]
[10]YE Dong-yi.New binary discernibility matrix and the computation of a core [J].Mini-Micro Systems,2004,25 (6):965-967(in Chinese).[叶东毅.一个新的二进制可辨识矩阵及其核的计算 [J].小型微型计算机系统,2004,25 (6):965-967.]
[11]QIN Zhi-hua,TANG Cheng-chao,WANG Jia-yang.A calculation for core attributes of inconsistent decision table [J].Computer Engineering and Applications,2005,41 (35):44-46.[覃志华,唐承超,王加阳.不相容决策表的核属性计算[J].计算机工程与应用,2005,41 (35):44-46.]
[12]QIN Chuan,CHEN Hai-jun,SHI Hua-ji,et al.Attribute reduction algorithm for inconsistent decision tables[J].Computer Engineering and Applications,2008,44 (24):162-164(in Chinese).[秦川,陈海军,施化吉,李星毅.不相容决策表的属性约简算法 [J].计算机工程与应用,2008,44(24):162-164.]
[13]GE Hao,YANG Chuan-jian,LI Long-shu.Efficient algorithm for computing core attributes [J].Computer Engineering and Applications,2010,46 (26):138-141 (in Chinese).[葛浩,杨传健,李龙澍.一种高效的核属性求解方法 [J].计算机工程与应用,2010,46 (26):138-141.]
[14]XU Feng-sheng.An improved approach to computer the feature core[J].Computer Engineering and Applications,2006,42(13):57-59 (in Chinese).[徐凤生.一种改进的属性核计算方法 [J].计算机工程与应用,2006,42 (13):57-59.]
[15]XU Feng-sheng.New discernibility matrix and computation of core [J].Computer Engineering and Applications,2007,43(1):38-40 (in Chinese).[徐凤生.一种新的可区分矩阵与求核方法 [J].计算机工程与应用,2007,43 (1):38-40.]

