一个高斯-赛德尔方法解方程组的有趣结果

冯天祥

（东莞职业技术学院，广东东莞 523808）

目前，线性方程组的求解一般不用直接法而采用迭代法，高斯-赛德尔方法是比较经典的一种迭代方法，而高斯-赛德尔方法的收敛性问题是该方法得以实施的前提.对于比较特殊的线性方程组用高斯-赛德尔方法求解的收敛性已经得到了非常完备的结论.

本文首先介绍了用高斯-赛德尔方法求解一般线性方程组的问题，其次介绍了与高斯-赛德尔方法收敛性有关的几个已有结果，然后给出了用高斯-赛德尔方法求解一般三对角方程组收敛的充分必要条件，最后在收敛的条件下给出用高斯-赛德尔方法求解一般三对角方程组的计算机实现.

1 高斯-赛德尔方法的已有结果

1.1 高斯-赛德尔迭代方法

设 A= (aij)n×n，其中 aii≠ 0(i = 1,2,...,n)，如果记

则解线性方程组AX=B的高斯-赛德尔方法的迭代格式为

其中记

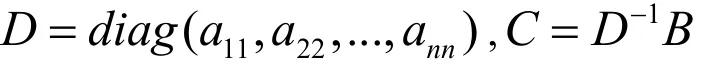
1.2 几个引理

引 理 1[1](36-80)对 于 迭 代 格 式X(k+1)= BX(k)+ C ，如果方程组X = BX +C有唯一解，则对于任意初始向量 X(0)，迭代格式X(k+1)= BX(k)+ C 格式都收敛的充分必要条件是其迭代矩阵G的普半径 ρ( G)＜1.

引理 2 解线性方程组AX=B的高斯-赛德尔迭代格式

X(k+1)=(I- L)-1UX(k)+(I- L)-1C 收敛的充分必要条件是

由引理1立即可得到引理2.

引理4[3-4]上（下）三角矩阵的特征值就是该矩阵的对角元.

2 用高斯-赛德尔方法求解三对角方程组的收敛性

定理 设有三对角矩阵

其中A可逆且 aii≠ 0(i = 1,2,...,n)，则用高斯-赛德尔方法求解线性方程组AX=B收敛的充分必要条件是

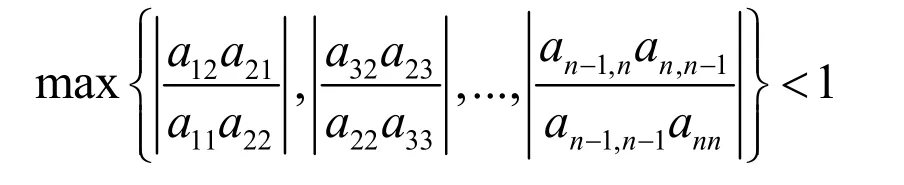
证明：由于严格下（上）三角矩阵

则高斯-赛德尔迭代矩阵为

所以由引理4知矩阵 (I-L)-1U的特征值分别为

所以

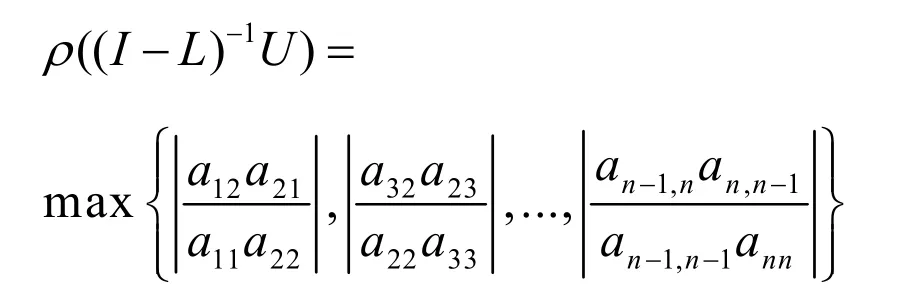
由引理 2知用高斯-赛德尔方法求解线性方程组AX=B收敛的充分必要条件是

3 用高斯-赛德尔方法求解三对角方程组的计算机实现

对三对角矩阵

其中A可逆且 aii≠0(i = 1,2,...,n).

用高斯-赛德尔方法求解线性方程组AX=B的步骤如下：

第一步：输入矩阵

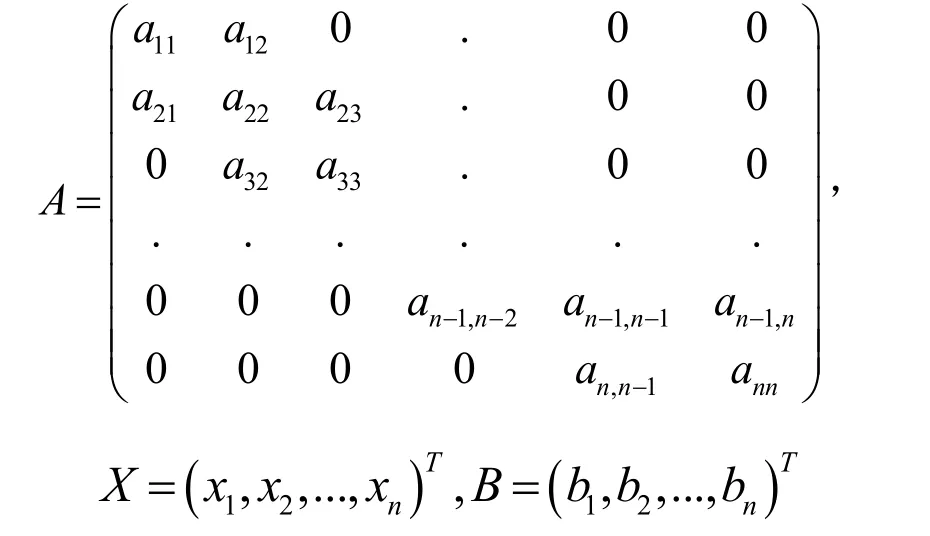
第二步：求出严格下（上）三角矩阵L,U

第三步：求出高斯-赛德尔方法的迭代矩阵

第四步：求出

第五步：迭代计算线性方程组AX=B的满足精度要求的近似解

1）写出 D =diag(a11,a22,...,ann)，计算

2）计算出 G =(I- L)-1U ,H =(I-L)-1C

[1]冯天祥.数值计算方法[M].成都：四川科学技术出版社，2003.

[2]李庆扬，王能超，易大义.数值计算[M].武汉：华中理工大学出版社，1998.

[3]王萼芳.高等代数教程[M].北京：清华大学出版社，2006.

[4]Feng Tian-xiang. Re-discussing Applications of Elementary Transformation in Matrix computation[J].重庆三峡学院学报，2008（3）.