一类变分不等式问题解的存在性
向以华
(重庆三峡学院数学与计算机科学学院,重庆万州 404100)
近年来,经典的变分不等式和相扑问题被推广于大量的来源于力学、物理学、非线性规划、经济与运输平衡、弹性接触问题.[1-2]本文利用不动点理论找出这类变分不等式问题解的存在性.并给出了一个特殊的结果.
1 预备知识
设V是一个实的Hilbert空间,K⊂V是一个非空的闭凸集,假设 A: V → V 强单调和Lipschitz连续, j: K → R 凸下半连续.考虑下述变分不等式,找u∈K使得
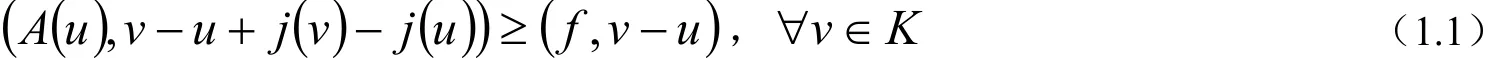
并且解u是Lipschitz连续地依赖于f.
定义1.1 设V是一个赋范空间.一个子集合K⊂V称为是凸的,如果
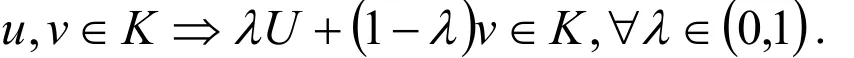
集合K⊂V称为是闭的,如果{vn}⊂K且vn→ v ,集合K称为弱闭的,如果{vn}⊂K且vn→v可推出v∈K,
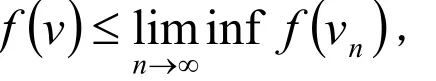
定义 1.3 设K⊂V是一个凸集.一个函数f: K→ R 称为是凸的,如果

函数 f称为是严格凸的,如果上式对u≠v,λ∈(0,1)时严格不等号成立.
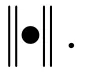

引理 1.1 设是一个赋范空间.假设是固有的,凸下半连续的则存在一个连续线性泛函lj∈V′和一个常数cj∈ R 满足
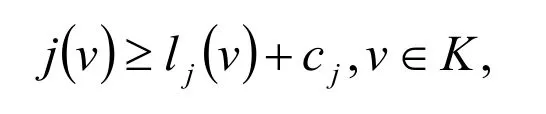
2 主要结果
定理 2.1 设V是一个实的Hilbert空间,K⊂ V是一个非空的闭凸集,假设 A:V → V强单调和Lipschitz连续, j: K → R凸下半连续.则对任意f∈V,变分不等式

存在唯一解,并且解u是Lipschitz连续地依赖于f.
证明.先证解的唯一性.假设(2.1)有两个解u1,u2∈ K.则成立

得 -(A(u1)-A(u2),u1-u2)≥0.
由A的强单调性,我们推出 u1= u2.
再证解的存在性.
将问题转化为等价的不动点问题.对任意的θ >0,问题(2.1)等价于
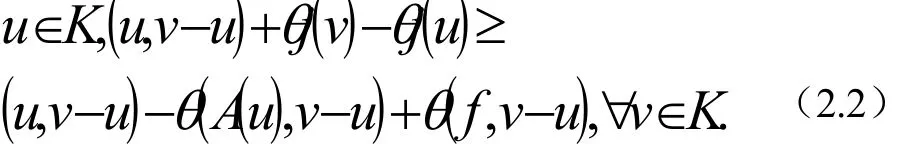
对任意的w∈K,考虑问题

这个变分不等式等价于极小值问题
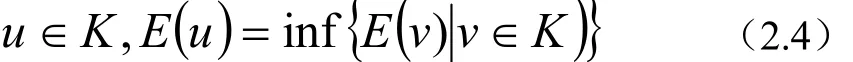
其中

利用结论:泛函 j( .)有一个有界的仿射泛函作为下界,即
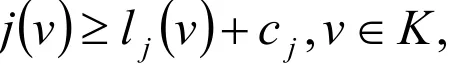
其中lj是V上的一个连续线性形,cj∈ R(见引理1.1),因此根据A,j,f上的假设条件,看到E严格凸,下半连续,且由性质
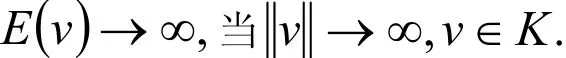
应用定理知道问题(2 .4 ),从而问题(2 .3)存在唯一解 w=Pθ(u).
显然投影算子 Pθ.的一个不动点是问题(2.2)的一个解,可以看出对充分小的θ >0,Pθ是压缩投影算子,由Banach不动点定理,投影算子Pθ存在一个不动点.
对任意 u1,u2∈K,记 w1=Pθ(u1),w2=Pθ(u2).
则
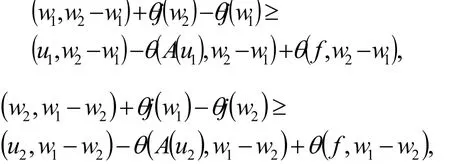
于是得到
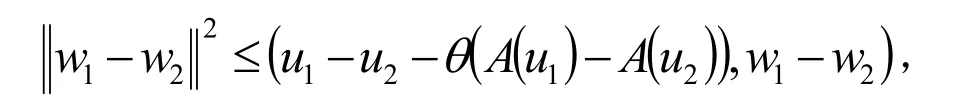
因此

而
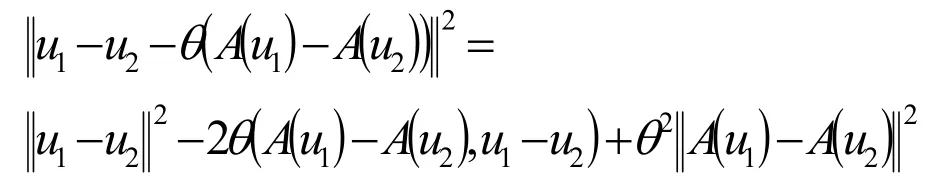
于是对 θ∈(0,2 c0M2),投影算子Pθ是Hilbert空间V上的一个压缩投影算子.
最后 f1,f2∈ V,记u1,u2为变分不等式(2.1)相应的解.则
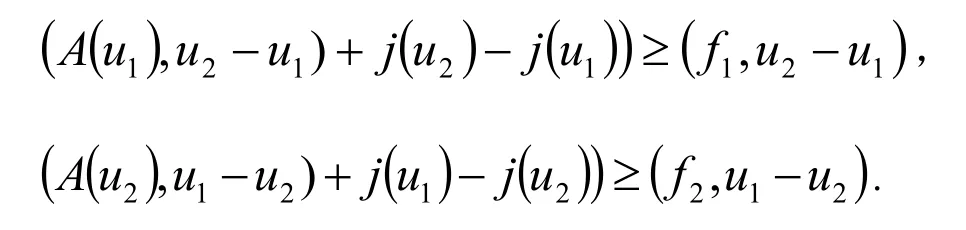
两个不等式相加,得

故

即解u依赖于f的Lipschitz连续性.
考虑定理(2.1)的一种特殊情况,f (v)≡ 0, v ∈ K,则(2.1)简化为
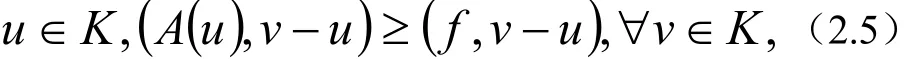
作为定理2.1的一个推论有:
定理 2.2 设V是一个实的Hilbert空间,K⊂ V是一个非空的闭凸集,假设 A:V → V强单调和Lipschitz连续,则对任意f∈V,变分不等式(2.5)存在唯一解u∈K,这个解是Lipschitz连续地依赖于f.
定理2.2是研究线性椭圆型边值问题唯一可解性的 Lax- Milg ram 引理的一个推广.
[1]张石生.变分不等式和相扑问题理论及其应用[M].上海:上海科技文献出版社,1991.
[2]Noor M A.Optimization,1994,30:323-330.
[3]Banach空间中的广义随机混合似变分不等式问题[J].四川大学学报(自然科学版),1999(5):829-833.

