基于OFDM技术FFT的FPGA研究

黄军友

（四川信息职业技术学院，四川广元 628017）

正交频分复用技术（Orthogonal Frequency Division Multiplexing，OFDM）较好地解决了由带宽限制、信道时变特性、噪声、干扰及多路径问题制约的通信质量和信道容量的发展问题.OFDM技术基本原理是把高速数据流分成若干低速数据流并行地在相互正交的子载波上传输，将频率选择性衰落信道转化成为若干平坦衰落子信道，[1]从而减少多径衰落的时间弥散，可以有效地对付多径衰落，对抗窄带干扰，提高传输速率.[2]OFDM可以采用FFT算法来实现，当子信道数目比较多的时候，采用FFT能减少系统的复杂度.本文主要研究2k/4k/8k多模式复用FFT的FPGA的实现.

1 设计思路

1.1 快速傅立叶变换

可知，8k傅立叶变换可由4*2k的傅立叶变换构成.2k的傅立叶变换可由128*16的傅立叶变换构成.128的傅立叶变换可进一步由16*8的傅立叶变换构成，即整个傅立叶变换可由基2基4的傅立叶变换构成.2k的FFT可以通过5个基4和一个基2变换实现；4k的FFT变换可通过6个基4变换实现；8k的FFT可以通过6个基4和一个基2变换实现.

1.2 基本运算单元

表1列出不同蝶形运算单元所需的运算次数.从基2到基4，实数乘、加法的运算次数发生了比较大的跳变，而从基4到基8以及基16运算次数变化的幅度不是很明显.从算法复杂性看，最优基为基4和基8.从控制角度看，基2算法最容易控制.基4算法控制复杂一些，仍然具有和基2算法的可类比性.8和基16算法的控制复杂度与基4相比跳变明显.考虑到运算速度和控制性的折衷，基4算法在基FFT处理实现中具有更高性价比.[3]

表1 蝶形运算单元的运算次数

其中，r=log2N

以4K点的FFT为例（时钟周期25 ns），如表2.

表2 运算效率

以基4作为基本的运算单元，至少需要流经基4单元6次.实际处理时间包括处理时延和存储时延，内部工作时钟至少为外部时钟的7倍，换成基16，内部工作时钟可以降为外部时钟的4倍，可以更为稳定的工作.本设计中，使用Stratix系列器件，逻辑资源较为充足.考虑速度、稳定性、通用性、所用资源等方面，采用4/2×4/2的蝶形运算单元结构，其基本的运算单元为基 4/2，在进行两次运算后进行存储调序的处理，减小了内部时钟的压力和控制的复杂度.

1.3 蝶形运算的位数

FFT运算结果的精度，与输入数据的位数及运算的过程中的位数有关，同时，和数据的表示形式也有很大关系.[4]通过仿真如图 1，固定 rom_bits的位数为 16，图中的曲线由上至下分别对应ram_bits由19至12变化.可以看到ram_bits大于16时，再增加其位数并不能带来更大的好处.因此在硬件实现代价和性能之间均衡，最终选取rom_bits=16，ram_bits=17.

图1 位数变化时信噪比变化图

1.4 8k点FFT实现

8k点的FFT可以通过低点数的FFT来实现.出于通用性和稳定性考虑，实际利用的运算单元是基16/8/4/2通用的运算模块，具体到8k点的实现就有16-8-8-8及16-16-16-2两种实现的方法.

图2分别表示了16-16-16-2和16-8-8-8分解方式下变换结果和Matlab工具箱中FFT函数比较的结果.从图中可以看到，两种方式均可以较好的完成 8k点的 FFT，信噪比均达到了 75 dB以上.16-16-16-2方式较16-8-8-8方式在信噪比上有约3 dB的增益.因此8k点变换的总体结构选用了16-16-16-2的分解方式.

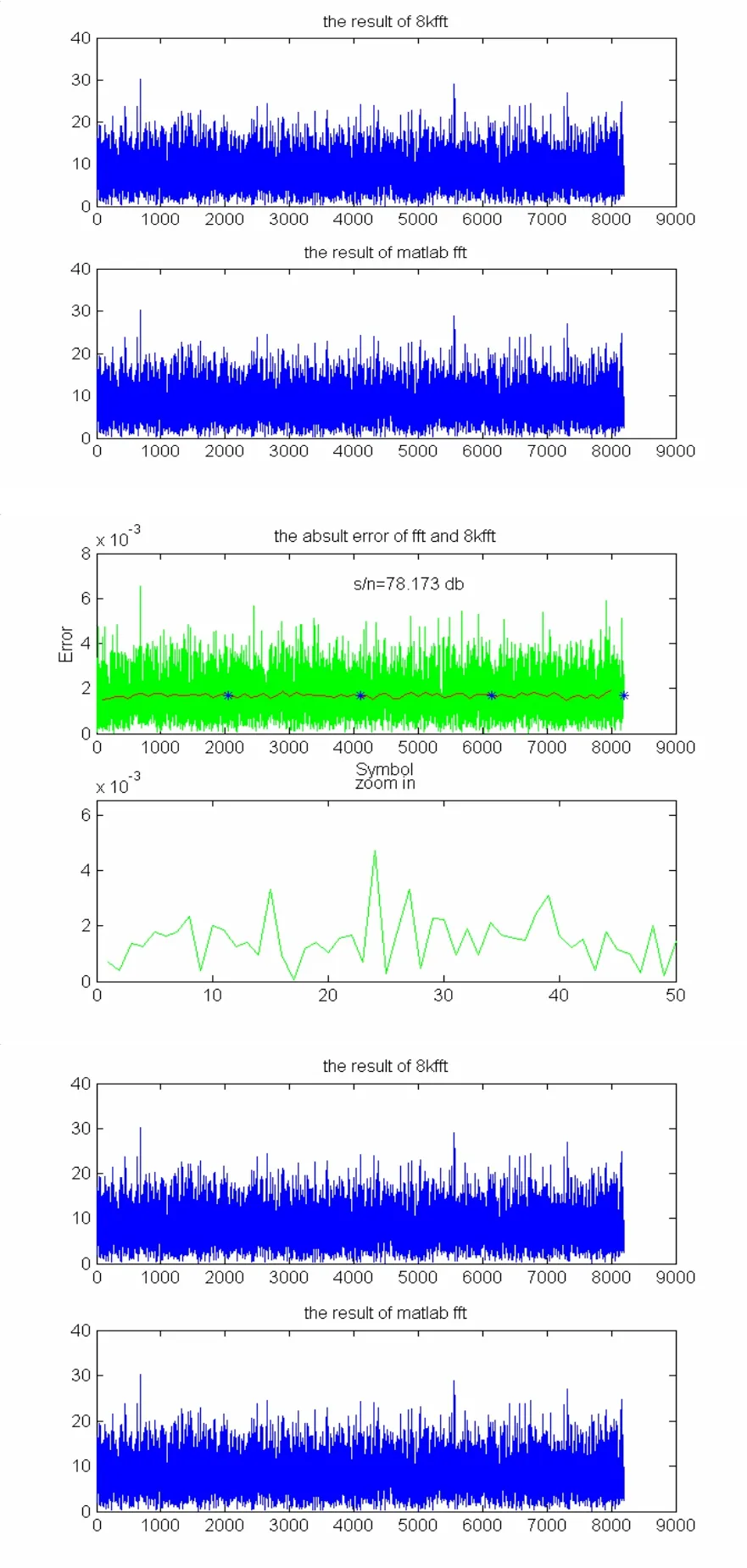
图2 两种分解模式的性能比较

1.5 FFT模块实现IFFT

实际实现中，在FFT运算模块的基础上，只需将输入序列进行取共轭后再进行FFT运算，输出结果再取一次共轭便实现了对输入序列的 IFFT运算.IFFT在FFT的基础上输入和输出均有一次共轭操作，但它们共用一个内核，这是十分方便的.而1/N实际上就是一个比例关系，可以根据输出数据的大小要求，选择一个合适的因子相除输出，来完成IFFT的运算.

2 FFT的FPGA实现

2.1 整体结构

FFT的基本结构可由基2/4模块，复数乘法器，存储单元和存储器的控制模块构成，整体结构如图3.

图3 FFT实现的总体框架

2.2 存储器的控制

通常外部输入数据的速度比内部数据处理速度慢.在输入一组数据时，在外部时钟的作用下，存入RAMa或RAMb其中之一，同时开始对两个RAM 中的另一个中的数据进行运算.输出部分的RAM与输入端类似，也是RAMc和RAMd轮流工作，如图4.为了适应多模式复用，设计指示信号，指示不同点数的输出时刻.接收端的RAM存储运算的结果，在指示信号的作用下输出数据.

在2k/4k/8k傅立叶变换中，要实现通用性，控制器是最主要的模块.2k，4k，8k变换有不同的内部运算时间和存储器地址，在通用性设计中，针对不同的点数设计不同的存储器存取地址，同时，在完成变换后，要对开始输出有用信号的时刻进行指示.

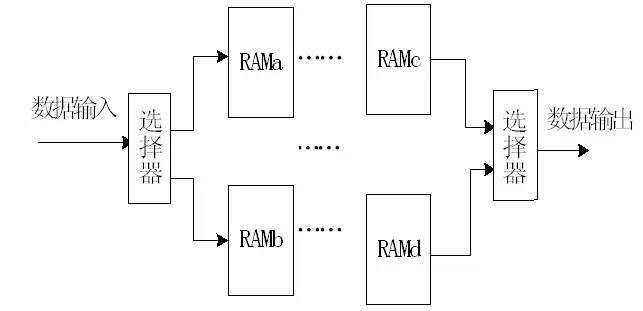
图4 输入输出控制

2.3 运算模块

图5是相应的硬件实现框图，此运算模块可以进行基16、基8、基4和基2的运算.其结构是由两级基 4/2复用的蝶形运算单元串行级联完成的.在第一级基2/4完成以后数据要经过RAM进行缓存以便调整顺序，调整完顺序后，以新的顺序输出，开始第2级基2/4运算.模块有两个数据输出端口.第一级运算完成后输出，可以完成基 2/4的运算，从第二级输出，可以完成16/8的运算，使此运算单元有很大的适应性.

图5 运算模块

2.4 FFT的地址

蝶形运算完成运算后，产生一定的逆序.为了保证顺序输入顺序输出，需要在RAM存取过程中进行地址变换.地址的产生可以采用不同的方式.[6]而本次实现中，由于芯片中的存储单元有限，采用了通过计数器计数，将计数结果按地址的规律进行变换的方法来产生所需的地址.针对不同的点数，给计数器设计不同的清零信号，完成多模式复用的设计.

2.5 旋转因子

其对称性表现为

表3 正余弦函数的对称性

对于2k/4k/8k的傅立叶变换来说，旋转因子只是对一个周期进行不同的分割.8k变换的旋转因子中包括了2k/4k的所有因子.实现中，ROM中存储了8k点FFT所对应的旋转因子.相对2k/4k变换来说，相对应的因子不是连续的，需要对8k的旋转因子按一定的规律抽取.抽取通过对读ROM的地址序列进行控制，可实现2k/4k/8k变换的通用性.

2.6 数据的锁存

通过选择器从RAM中取数据的同时，从ROM中取旋转因子.在数据和旋转因子进入基4运算单元后，首先进行锁存，然后并行送入基4的运算部分，以达到数据和旋转因子的同步，如图6（a）.而输出时，为达到流形输出的效果，也需要进行锁存，如图6（b）：

图6 数据的锁存

2.7 2的幂次点数的FFT设计

本次实现，只是将2k/4k/8k点的FFT设计在一个工程中.当需要16点、256点、1024点等点数的FFT变换时，分别需要2个基4单元，4个基4单元以及5个基4单元，而8点，32点、512点的FFT变换，分别需要1个基4和1个基2单元、2个基4和1个基2单元、4个基4和1个基2单元.都可以归结成基4基2单元，在具体实现中，可以控制数据流过蝶形运算单元的次数来完成.

2.8 硬件的选择及性能研究

ALTERA公司的Stratix系列中的EPLS25芯片是现场可编程门阵列（FPGA），能满足较高速度的需要.芯片内部集成了25660个逻辑单元（LE），1899K RAM比特.芯片中专用DSP处理模块，对乘法器的实现具有快速，准确的优势.EP1S25含224个M512，均匀分布在片内，可用于需要大量小规模存储器的场合.EP1S25含138个M4K，每块大小为4608个比特（含512检验位）.EP1S25还有两个大容量MegaRAM，每块含576K个比特（64K校验位），适用于需要大容量RAM的数据转发，视频缓存等应用场合.[9]这些片内 RAM具有很高的灵活性和很强的实用性，在设计中可以用作RAM，ROM，FIFO等等存储类型.同时在应用时，可以对其存储数据的总线宽度，存储的深度及读、写产生的时延等等进行设定.

除了一些专用引脚外，FPGA上几乎所有的引脚均可供用户使用，这使得FPGA信号处理方案具有非常高性能的I/O带宽.大量的I/O引脚和多块存储器可让设计获得优越的并行处理性能.独立的存储块可作为输入/工作存储区和结果缓存区，这使得I/O可与FFT计算同时进行.

在实现的时间方面，以一个4096点的FFT为例，在4096个时钟周期内完成.若采用10 MHz的输入时钟，变换时间在300 us左右，而最新的FPGA使用了MultiTrack互连技术，可以在250 MHZ以下的频率稳定的工作，对于FFT的实现时间可以大大地缩小.

3 测试和验证

如图7所示，验证的过程分为仿真和实测，比较的基准是Matlab工具箱中的FFT函数.本次设计共使用了6 295个逻辑单元，24个DSP模块，1 015 808 bit的存储单元，信噪比达到了75 dB以上，可以满足大多数情况下的应用要求.

图7 测试与验证流程

[1]谭泽富.一种OFDM系统中的频偏估计方法[J].重庆三峡学院学报，2006（3）.

[2]党向东.专用 FFT实时信号处理器的硬件实现研究[J].锦州师范学院学报（自然科学版），2003（2）.

[3]李成诗，初建朋，李新兵，等.基于CORDIC的一种高速实时定点 FFT的 FPGA实现[J].微电子学与计算机，2004（4）.

[4]李小进，初建朋，赖宗声，等.高速基2FFT处理器的结构设计与 FPGA实现[J].电路与系统学报，2005（5）.

[5]Richard B. Ertel, “Generation of Two Equal Power Correlated Rayleigh Fading Enelopes”, IEEE Communications Letters, 1998,10:pp276-278.

[6]王凯，葛建华，梁锡林.OFDM调制中高速FFT处理器的设计与实现[J].中国有线电视，2006（1）.

[7]田丰，邓建国，贾治华，等.FFT算法的一种FPGA实现[J].现代电子技术，2005（8）.

[8]蒋冰，刘怀宇.基于存储器的3780点FFT的FPGA设计和实现[J].中国有线电视，2005（23）.

[9]顾晴茹，周玉洁.OFDM系统中高速FFT处理器的FPGA实现[J].信息技术，2005（12）.