姿态检测用地磁图的线性样条组合插值算法

刘建敬,张 合,程 翔

(南京理工大学智能弹药技术国防重点学科实验室,江苏南京 210094)

0 引言

地球磁场是天然存在的基本矢量场,连续分布,而且缓慢变化,为航空、航天和航海提供很好的参考基准,可应用于导航定位和姿态控制[1-2]。基于地球磁场的弹体姿态角检测技术具有可靠性高、抗高过载和冲击、易于小型化和无源自主等特点,对常规弹药简易制导技术的发展具有重要意义,日益引起国内外的关注和研究,比如美国阿连特技术系统公司设计的姿态测量系统,就是利用地球磁场测量弹体滚转角[3-4]。

弹体滚转角检测系统在计算角度之前,需要由雷达或者GPS给出弹丸的实时位置信息,通过预先装入地球磁场模型或者地磁图来实时获取地球磁场信息[5]。由于地球磁场模型过于复杂,计算量太大,所以建立地磁图更合适。但是弹药发射地点不确定,并且常规弹药空间有限,姿态角检测系统无法存储大量的地磁图信息,只能根据发射点位置和弹药射程所在区域,在发射前将装入该区域的地球磁场参数,然后结合弹丸的位置,通过插值方法实时计算地球磁场矢量。相对于常规弹药高转速对姿态角检测的实时性要求,常用的地磁图插值方法(比如克里金插值法、径向基函数法和BP神经网络法、曲面插值法和支持向量机等[6-10])虽然精度高,但是算法仍较复杂,实时性差。双线性插值方法[11],虽然能够满足实时性的要求,但是插值精度较低。

针对双线性插值地磁图精度低的问题,提出了地磁图的线性样条组合插值算法,并通过仿真和误差分析进行验证。

1 地磁图插值方法比较

双线性插值是线性插值在两维空间的扩展,即在两个方向上分别进行线性插值,其函数形式为[11]:

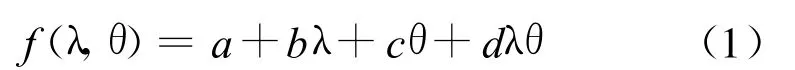
由式(1)看到,双线性插值方法简单,只有4个系数,整个运算仅需要进行3次加法和3次乘法,计算速度快。

线性样条组合插值是对双线性插值的改进,在一个方向上进行线性插值,在另一个方向上进行三次样条插值,其函数形式为:

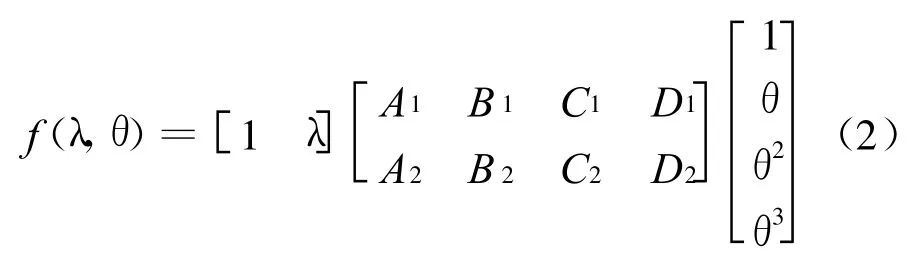
由式(2)看到,线性样条组合插值有8个系数,整个运算需要进行7次加法和7次乘法,精度高。

与双线性插值相比,地磁图的线性样条组合插值方法虽然运算速度稍微降低,但是插值精度高,相邻插值区域之间连续性好。

2 地磁图的线性样条组合插值

2.1 地磁图线性样条组合插值的原理与特点

根据地球磁场总强度的等值线图[12-13]看到,地球磁场具有沿经线方向变化快,沿纬线方向变化慢的特点。结合地球磁场变化的特点,地磁图的线性样条组合插值,在经线方向上采用精度较高的三次周期样条插值,在纬线方向上采用线性插值。

在绕地球一周的经线圈上,地球磁场的变化具有周期性和连续性的特点,这个特点符合三次样条插值的周期边界条件。在经线方向上,采用三次周期样条插值,不仅能够准确描绘地球磁场的变化趋势,而且能够保持地球磁场连续性的特点。在沿纬线方向上,采用线性插值可以提高计算速度,并且保持较高的插值精度。

地磁图的线性样条组合插值算法与地球磁场的变化特点相结合,具有插值精度高和计算速度快的特点,并且能够保持地球磁场变化的连续性。

2.2 组合插值系数计算公式

根据线性样条组合插值形式可知,计算某区域地球磁场,必须首先得到该区域组合插值的8个系数,下面对插值系数的计算公式进行推导。

假设将绕地球一圈的经线分成n段,绕地球半圈的纬线分成m段,这样地球就分成m×n个区域。假设其中某个区域四个顶点的分别为()、和θj+1),其中 i=0,1,…,m;j=0,1,…,n;λ和θ分别代表经度和纬度,每个顶点对应的地球磁场强度依次为和如图 1 所示 。那么,该区域内任一点R的组合插值函数如式(3)所示。

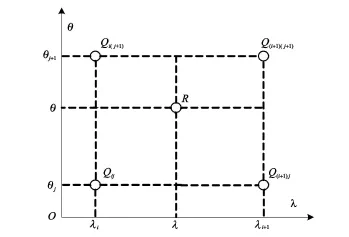
图1 插值区域示意图Fig.1 Schematic of interpolation area

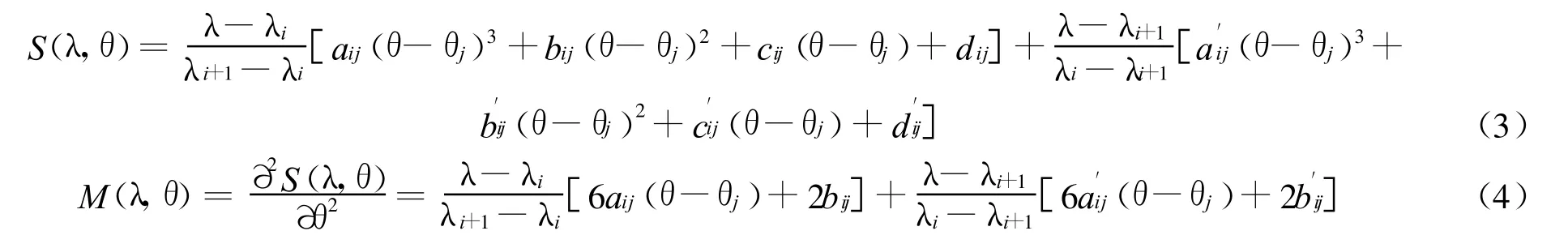
式中,S(λ,θ)为线性样条组合插值函数,M(λ,θ)为插值函数对 θ的二阶偏 导数,aij、bij、cij、dij、、和为待定系数 。

式中,hj=θj+1-θj,j=1,2,…,n-1。

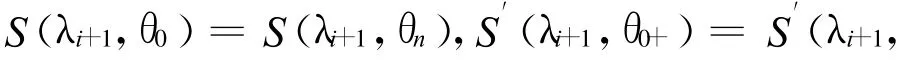
同理,根据经线λi一周上各节点处的地球磁场强度Fij(j=0,1,…,n)和周期边界条件,可以得到和。

由此得到该区域的线性样条组合插值函数S(λ,θ),其矩阵形式如下如式(2)所示。式(2)中的8个系数通过展开式(3),并根据待定系数法由 aij、bij、cij、dij、a和计算得到,如式(6)所示,式中=-。

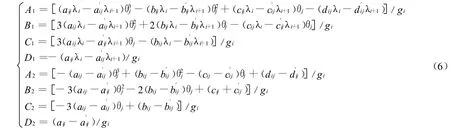
3 组合插值仿真

地球磁场有3个正交分量:北向分量X、东向分量Y和竖直分量Z,并且地球磁场的总磁场强度F、水平分量H,磁偏角D和磁倾角I都可以由这三个正交分量计算得到[13]。本文以IGRF模型为参考依据,对南京所在区域(N30°～ N35°,E115°～ E120°)的地球磁场X、Y和Z分量进行线性样条组合插值仿真计算。

首先 ,通过 IGRF 模型 ,计 算 E115°和 E120°圆周上各个节点处的X、Y和Z分量,并计算该区域每个分量对应的8个线性样条组合插值系数,如表1所示。

然后,以0.1°为步长,分别沿经线和纬线方向,将该区域分成50×50个网格,根据已知的X、Y和Z分量线性样条组合插值函数,计算各个网格节点上的对应的地球磁场分量。图2所示为通过线性样条组合插值计算得到的地球磁场X、Y和Z分量等值线图。

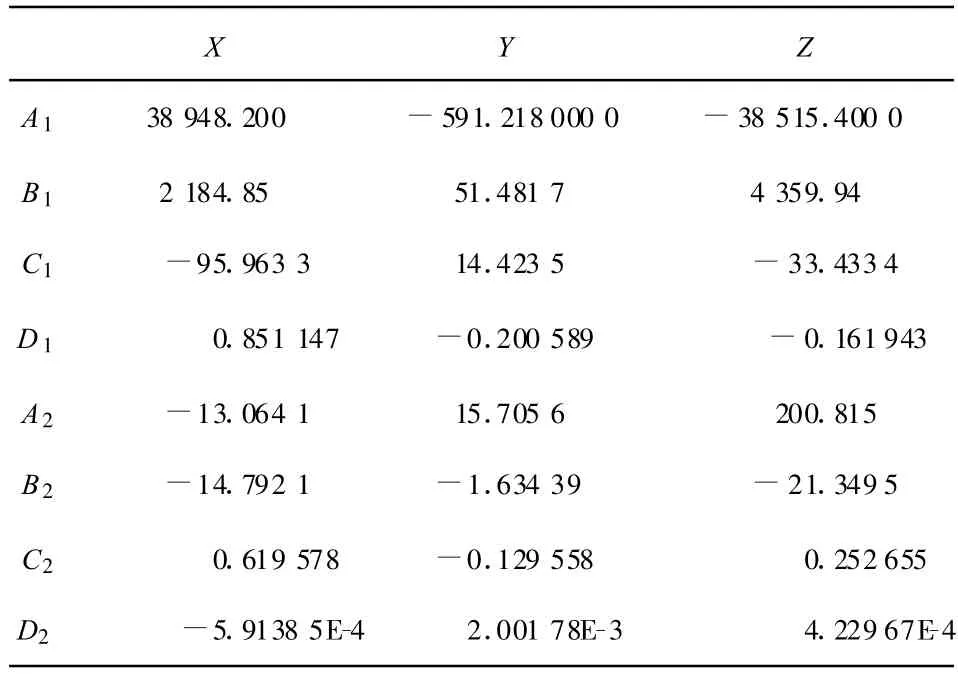
表1 线性样条组合插值系数Tab.1 Coefficients of linear spline combination interpolation

由此可知,仅需要将每个区域地球磁场分量的8个插值系数预先存储起来,根据弹体的经纬度信息, 便可以迅速计算得到该位置的地球磁场信息。

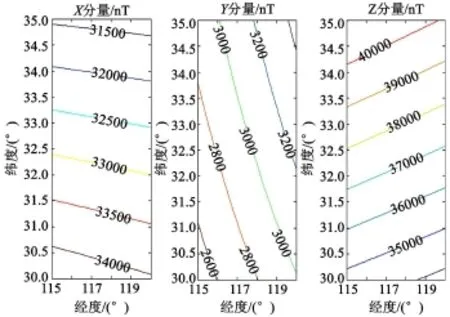
图2 X、Y和Z分量等值线图Fig.2 Isoline maps of components of X,Y and Z

4 组合插值误差分析

以赤道与E0°～E180°线的交点为起点,沿经线方向顺时针绕地球一周为正方向,纬度的变化范围为 0°～360°,分别沿经线和纬线方向 ,以 5°为步长,将地球划总共划分成72×36个区域。以中国在内的(N0°～ N60°,E60°～ E140°)区域为研究对象 ,该区域可划分为12×16个小区域。通过IGRF模型计算每个节点上的总磁场强度,如图3所示。根据总磁场强度的变化发现,地球磁场变化最强烈的小区域为(N35°～ N40°,E135°～ E140°)。所以,根据该区域的地球磁场强度进行线性样条组合插值的误差分析。

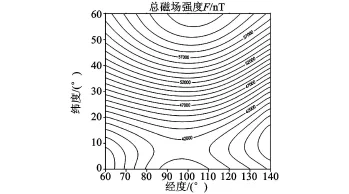
图3 总磁场强度 F等值线图Fig.3 Isoline map of total intensity F

首先,以0.1°为步长,分别沿经线和纬线方向,将该区域分成50×50个网格,分别通过线性样条组合插值和IGRF模型计算各个网格节点上地球磁场的 X、Y和Z分量。

其次,以IGRF模型计算的地球磁场分量为该区域的理论值,计算各个网格节点上地球磁场X、Y和Z分量线性样条组合插值数据的相对误差,如图4所示。地球磁场分量的相对误差在经度方向基本呈对称分布,X、Y和Z相对误差分别在0.030%、0.765%和0.032%以内。然后,根据已知 X、Y和Z分量,计算地球磁场的另外4个特征分量,分析线性样条组合插值的精度,并与双线性插值结果进行比较,如表2所示。与双线性插值相比,组合插值的精度基本提高了一倍以上,其中F和H分量的相对误差分别小于0.003%和0.044%、D和I分量的角度误差分别小于 0.057°和 0.02°。

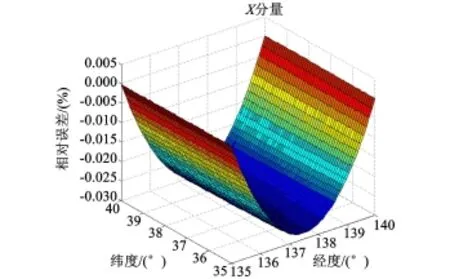
图4 X分量的相对误差Fig.4 Relative error of component

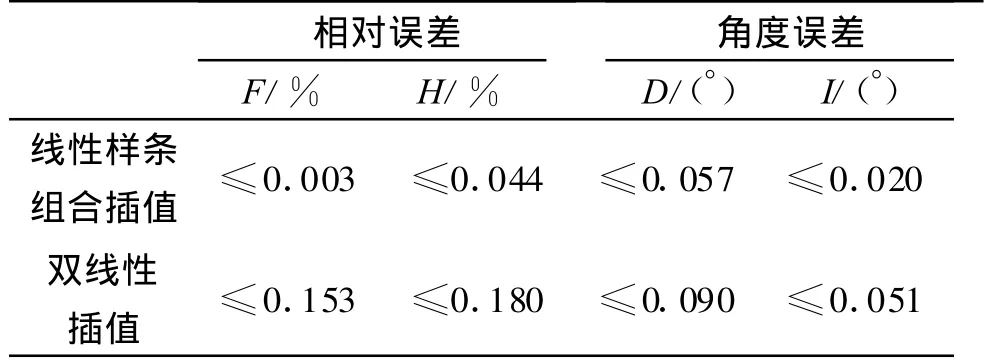
表2 地球磁场插值误差Tab.2 Interpolation errors and calculation speed of geomagnetic field

由此可知,与双线性插值相比,地球磁场的线性样条组合插值方法的精度得到大幅提高,能够更好地满足获取地球磁场信息的实时性和精确性要求。

5 结论

本文通过对双线性插值和线性样条组合插值的比较和分析,结合地球磁场变化的特点,提出了弹丸滚转角检测的地磁图线性样条组合插值方法。该方法在经线方向上采用三次周期样条插值,在纬线方向采用线性插值的组合插值算法,并推导了组合插值系数的计算公式。仿真和误差分析表明:预先装入8个插值系数,线性样条组合插值仅需要7次加法运算和7次乘法运算便可以计算出地球磁场的一个分量,并且精度比双线性插值提高了近一倍以上。由此表明,线性样条组合插值计算速度快,精度较高,能够保证弹体滚转角检测系统实时准确地获取地球磁场信息。

[1]Goldenberg F.Geomagnetic navigation beyond the magnetic compass[C]//Position Location and Navigation Symposium.Washington:IEEE,2006:684-694.

[2]郭才发,胡正东,张士峰,等.地磁导航综述[J].宇航学报,2009,(4):1 314-1 319.GUO Caifa,HU Zhengdong,ZHANG Shifeng,et al.A Survey of geomagnetic navigation[J].Journal of Astronautics,2009,(4):1 314-1 319.

[3]高峰,张合,程翔,等.弹道修正引信中的地磁信号及其抗干扰研究[J].弹道学报,2008(4):45-48.GAO Feng,ZHANG He,CHENG Xiang,et al.Research on geomagnetic signal and its anti-interference for fuze of trajectory correction projectile[J].Journal of Ballistics,2008(4):45-48.

[4]Johnson,Lyle H Kurschner,Dennis L.Roll orientation using turns-counting fuze:EP,1813905[P].2007-08-01.

[5]史连艳,杨树兴,张夏庆.M R/GPS制导在旋转火箭弹中的应用分析[J].弹箭与制导学报,2006(2):1 145-1 147.SHI Lianyan,YANG Shuxing,ZHANG Xiaqing.Analyzing of MR/GPS guiding applied in rotating rocketpowered missile[J].Danjian Yu Zhi Dao Xuebao,2006(2):1 145-1 147.

[6]杨功流,张桂敏,李士心.泛克里金插值法在地磁图中的应用[J].中国惯性技术学报,2008(2):162-166.YAGN Gongliu,ZHANG Guimin,LI Shixin.Application of universal Kriging interpolation in geomagnetic map[J].Journal of Chinese Inertial Technology,2008(2):162-166.

[7]黄学功,房建成,刘刚,等.地磁图制备方法及其有效性评估[J].北京航空航天大学学报,2009(7):891-894.HUANG Xuegong,FANG Jiancheng,LIU Gang,et al.Geomagnetic mapping and validity estimation[J].Journal of Beijing Uneversity of Aeronautics and Astronautics,2009(7):891-894.

[8]乔玉坤,王仕成,张金生,等.基于 BP网络的地磁基准图制备及其精度评价[J].中国惯性技术学报,2009(1):53-58.QIAO Yukun,WANG Shicheng,ZHANG Jinsheng,et al.BP neural network based preparation method of geomagnetic reference map and its accuracy evaluation[J].Journal of Chinese Inertial Technology,2009(1):53-58.

[9]Qiao Yukun,Wang Shicheng,Zhang Jinsheng,et al.Surface spline based constructing method for geomagnetic reference map[C]//International Conference on Information and Automation.US:IEEE,2009:708-711.

[10]Wang Shicheng,Qiao Yukun Zhang Jinsheng,et al.SVM based construting method for geomagnetic reference map[C]//Pacific-Asia Conference on Circuit,Communications and System.US:IEEE,22009:579-581.

[11]陈丽.基于三维磁探测的弹丸姿态角检测技术研究[D].南京:南京理工大学,2009.

[12]Regan Robert D.An overview of geomagnetic field models,ADA102946[R].US:Phoenix Corp Falls Church VA,1980.

[13]Susan Macmillan.Earth's magnetic field[M/OL].Oxford,UK:Eolss Publishers,2004[2010-6-11].http://www.eolss.net/ebooks/Sample%20Chapters/C01/E6-16-04-01.pdf.

[14]文世鹏,张明.应用数值分析[M].第三版.北京:石油工业出版社,2005.