分数阶傅里叶变换与虚拟阵列相结合的波达方向估计

金 翔,张天骐,侯瑞玲,高永升

(重庆邮电大学信号与信息处理重庆市重点实验室,重庆 400065)

0 引言

宽带线性调频(LFM)信号在通信、雷达、声纳、生物医学以及地震勘测等系统中都有广泛的应用,针对此类信号的波达方向(DOA)估计问题也日益受到人们的重视。时频分析是处理非平稳信号的有效手段,Belouchrani和Amin等提出了空间时频分布(spatial time-frequency distribution,STFD)的概念,在DOA估计中取得了优于传统方法的性能[1-2]。然而,常规的算法可以实施的前提条件是入射信源之间弱相关或不相干,而实际的环境中,很多情况下会有相干信号,也就不能进行正确的估计。文献[3]提出了时频相干信号子空间法,实现了宽带非平稳信号源的阵列信号DOA估计,但需要来波方向的初始估计,还存在稳健性不好和运算量巨大等缺点。文献[4]提出了在分数阶Fourier变换(FRFT)结合前后向平滑技术进行宽带相干LFM信号的DOA估计,但此方法减少了阵列的孔径,使N个阵元最多只能估计-1个相干信号,其精度等参数也存在一定的限制。为此,本文提出了FRFT与虚拟阵列相结合的相干LFM信号DOA估计方法。

1 宽带LFM信号估计的基本概念

1.1 分数阶Fourier变换的阵列信号分析

信号x(t)的分数阶傅里叶变换定义为[5]:

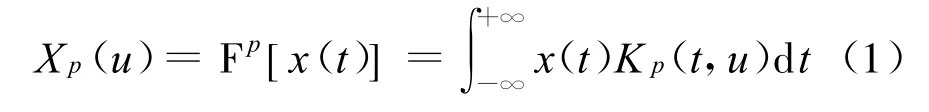
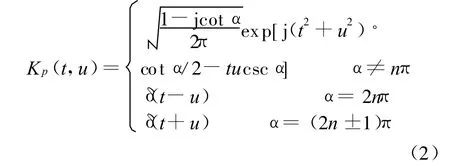
信号x(t)的FRFT是线性变换,它和Wigner-Ville分布(WVD)的关系可解释为时频平面的旋转算子,这一特性决定了FRFT特别适合于处理LFM类信号。如图 1所示,一个有限长 LFM信号的Wigner分布在时频平面呈现为斜直线的背鳍形分布,因此,若在与该斜直线相垂直的FRF域上求信号的分数阶Fourier变换,则在该域的某点将出现明显的峰值。而噪声的能量均匀地分布在整个时频平面内,在任何的分数阶傅里叶域上均不会出现能量聚集。因此,FRFT在某个分数阶Fourier域中对给定的LFM信号具有最好的能量聚集[5]。

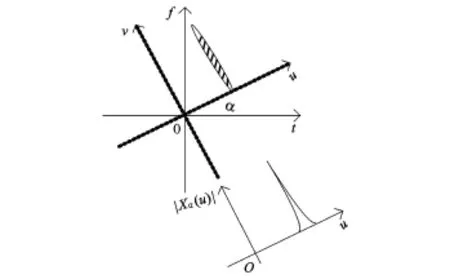
图1 LFM信号的时频分布及其在FRF域上的投影Fig.1 LFM signal in the Time-Frequency distribution and projection of FRF domain

由式(1)FRFT的定义,可知阵元信号sq(t)的p阶FRFT为:

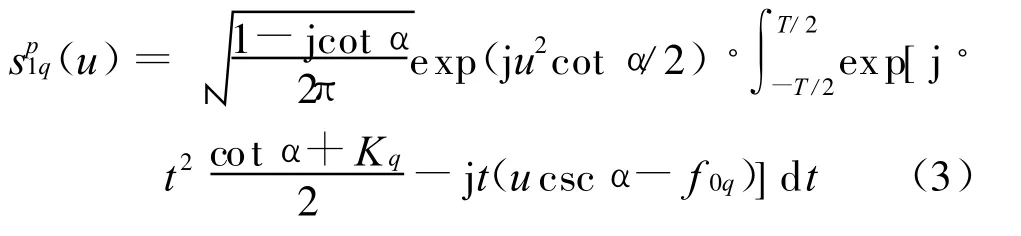
式中,T为观测时间,在(α,u)平面上,运用分级计算迭代搜索方法对sp1q(u)进行峰值点的二维搜索,以提高FRF T的搜索效率,即确定分数阶的搜索范围(a,b),确定初始步长Vp1=0.1,估计出分数阶的初始值为p1,再进行二次搜索范围(p1-0.1,p1+0.1),确定初始步长Vp2=0.01,估计出分数阶的初始值为p2,再进行三次搜索范围(p2-0.01,p2+0.01),确定初始步长Vp3=0.001,直至达到所要求的精度。得到峰值点的位置αq和u1m,则可得信号的调频斜率和初始频率估计[5]

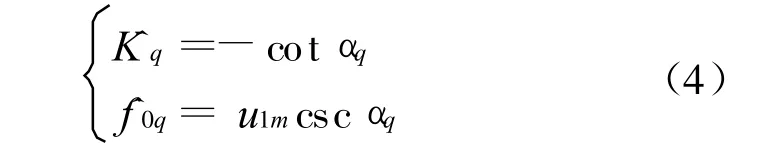
也就是说,当旋转角度α=-arccot Kq时,sp1q(u)有最佳的能量聚集,LFM信号有最大的峰值为:

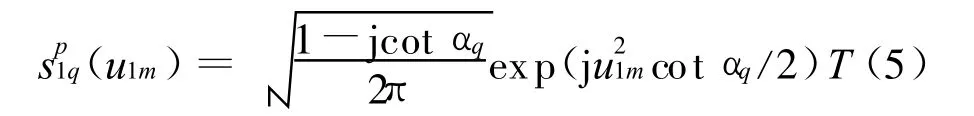
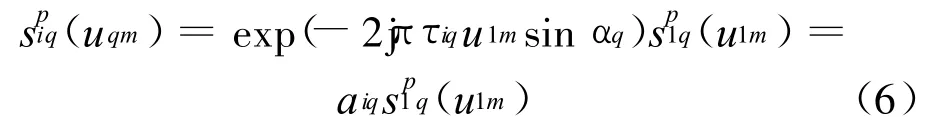
式中 ,aiq=exp(-2jπτiqu1msin αq),q=1,2,…,Q 。

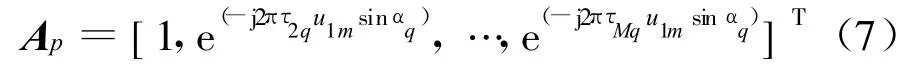
由分数阶Fourier域对应的宽带LFM信号的方向向量 Ap,可得到天线阵列的观测信号在分数阶Fourier域矢量表达式

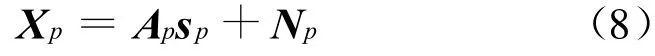
式中,

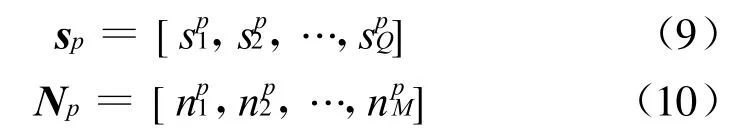
1.2 宽带LFM信号的阵列模型

阵列模型为M个阵元的均匀线阵(ULA),阵元间距为d,如图2所示。

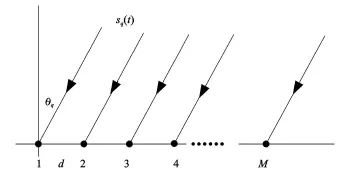
图2 均匀线阵结构示意图Fig.2 The ULA and array model

假设有Q个宽带LFM信号,入射角分别为θ1,θ2,…,θQ,Q ＜M。如果把第一阵元作为参考阵元,则第i个阵元上的观测信号可以表示为:

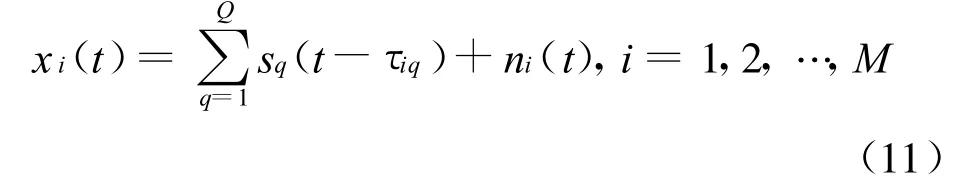
式中 ,

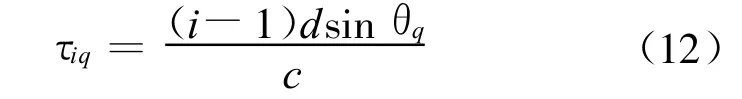
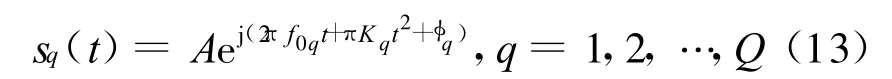
1.3 虚拟阵列的定义[7]

虚拟阵列变换法的基本原理是每次将阵列等间距地向右平移一个等距d,依次形成第2,3,…,M′个阵列,如图3所示。

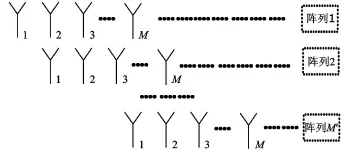
图3 虚拟阵列变换法原理图Fig.3 Virtual array transformation action principle

2 FRFT结合虚拟变换法的宽带相干LFM信号的DOA估计算法

空间平滑术是以损失阵列的孔径为代价的,为估计Q个相干信号,阵列的最小阵元数必须大于2Q个,很明显阵列的孔径损失了一半。

现在我们把整个阵列等间距地向右平移一个d,则平移L-1次后,得第L(1≤L≤M′)个阵列协方差矩阵为:

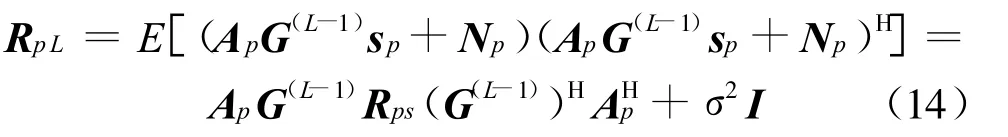
式中,H表示转置,σ2I为噪声FRF域的协方差矩阵,G(L)表示Q×Q的对角矩阵的L次方,且

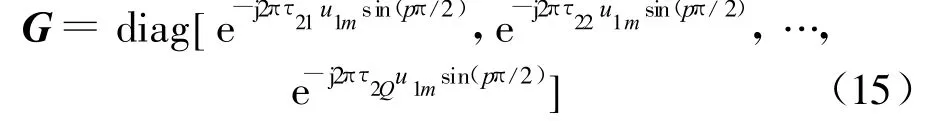
整个线阵的协方差矩阵定义为各子阵协方差矩阵Rp1,Rp2,…,RpM′的平均,也就是

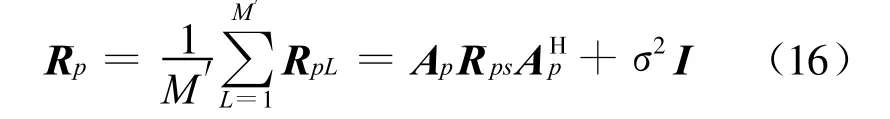
式中,β=[β1β2…βQ]为一个行向量,所以有

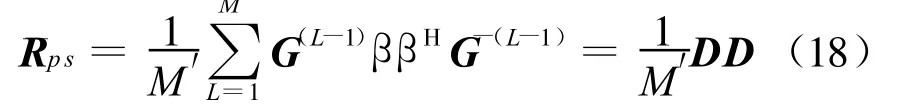
这里 D=[β,Gβ ,…,G(L-1)β]。

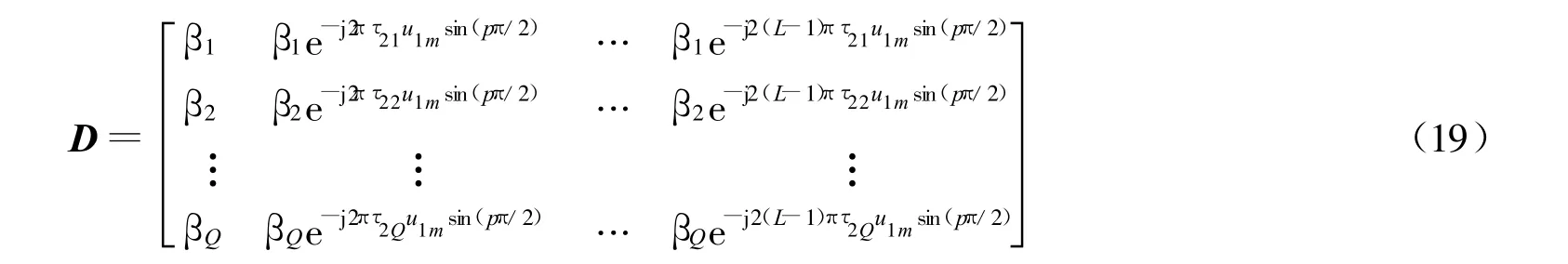
由式(12)中的延时特性,很明显,只要各个信号不是来自同一个方向,矩阵D便为满秩,因而矩阵和矩阵都为满秩,即

基于以上分析,可以总结分数阶Fourier变换和虚拟阵列变换相结合的宽带相干 LFM信号的DOA估计算法步骤如下:

1)对参考阵元上的接收相干信号进行分数阶傅里叶变换;

2)确定FRFT域峰值点的位置和对应的方向向量;

3)用虚拟阵列变换算法解相干;

4)运用常规的MUSIC算法或ESPRIT算法进行DOA估计。

3 仿真实验

由于MUSIC算法进行DOA估计时要进行空间谱峰搜索,相对计算量太大,而ESPRIT算法估计信号的DOA,将信号参数的搜索过程转变为了计算过程,降低了运算量的同时减小了算法对硬件的要求。于是在下节仿真实验二中,我们采用ESPRIT算法代替MUSIC算法进行仿真,以提高运算速度。

1)仿真实验一

假设两个有相同时频分布的宽带相干LFM信号 ,信号 1:s1(t)=A1exp(jπ0.1t+jπ0.001t2),入射角 θ1=30°;信号 2:s2(t)=A2exp(jπ0.1t+jπ 0.001t2),入射角θ2=70°。信号的幅度为 A1=2A2=1,快拍数N=200,SNR=2 dB,天线为均匀直线阵,且阵元数 M=9。分数阶Fourier域的表示如图4所示,从图中可以看出,两信号出现峰值时有相同的分数阶p,两信号不能进行分离。此时在分数阶Fourier域进行前后向平滑技术处理,若取子阵元数为M0=6,则前后向平滑的次数为L=4。再用MUSIC算法对信号进行DOA估计,空间谱如图5所示。若采用分数阶Fourier变换和虚拟阵列的宽带相干LFM信号的DOA估计算法进行DOA估计,结果如图5中的实线所示。

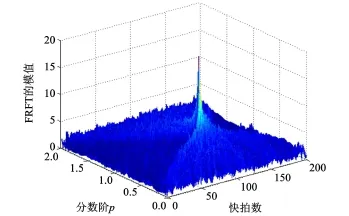
图4 分数阶Fourier域的相干宽带 LFM信号Fig.4 Wideband coherent LFM signals in FRF domain

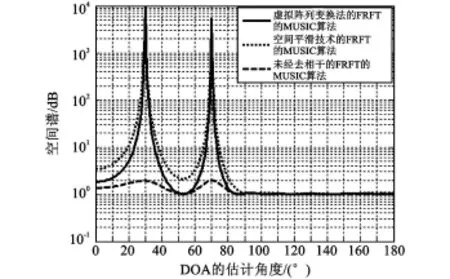
图5 基于FRFT的三种算法对相干信号源的估计Fig.5 The estimation of coherent signals source with three algorithms based on FRFT

从图5中可以看出,空间平滑技术的性能要优于未来经过处理的FRFT的宽带相干LFM的MUSIC算法,而用虚拟阵列空间变换法的分数阶Fourier域的宽带相干LFM信号的DOA估计算法比空间平滑技术要好。为了更进一步地说明问题,同时提高计算速度,我们进行仿真实验二。

2)仿真实验二

设和仿真实验一具有相同参数的信号,输入SNR范围为-4～10 dB,间隔2 dB,分别运行400次Monte Carlo实验,图6、图7分别为信号1和信号2的方向估计角均方误差随信噪比变化的特性图。

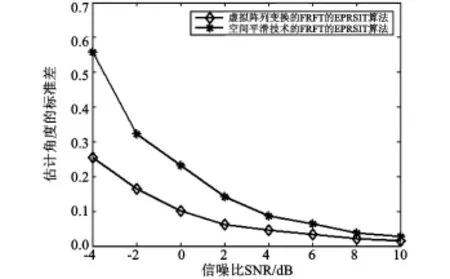
图6 信号源1(30°)均方误差随信噪比变化图Fig.6 MSE of signal 1(30°)

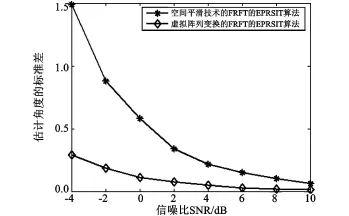
图7 信号源2(70°)均方误差随信噪比变化图Fig.7 MSE of signal 2(70°)

从图6和图7可以明显看出:虚拟空间阵列变换的FRFT的EPRSIT算法和空间平滑技术的FRF T的EPRSIT算法都可以估计宽带相干LFM信号DOA,但前者的性能特性明显优于后者,并且随着信噪比的降低,前者比后者的优势更加明显。

4 结论

本文提出了一种基于分数阶傅里叶变换和虚拟阵列变换法相结合的宽带相干 LFM信号的DOA估计算法。该方法首先将天线阵的观测信号变换到分数阶Fourier域(FRF域),然后用虚拟阵列变换法对相干信号进行解相干,再用ESPRIT算法进行波达方向估计。理论分析和仿真结果表明:与空间平滑技术的FRFT的EPRSIT算法相比,在低SNR下,性能特性明显要好,并且用分级计算迭代法大大减少了计算量。同时,不损失阵列的孔径,使 N个阵元可估计相干信号源数目达N-1个,提高了阵元数的利用率。

[1]Belouchrani A,Amin M G.Time-frequency music[J].IEEE Signal Processing Letters,1999,6(5):109-110.

[2]Amin M G.Spatial time-frequency distributions for direction finding and blind source separation[J].In Proc SPIE,1999,37(23):62-70.

[3]张艳红,齐林,穆晓敏,等.基于分数阶Fourier变换的WLFM信号DOA估计[J].信号处理,2005,21(4):57-60.ZHANG Yanhong,QI Lin,M U Xiaomin,et al.DOA estimation of WLFM signal based on fractional Fourier transforms[J].Signal Processing,2005,21(4):57-60.

[4]QU Haitao,QI Lin,MU Xiaomin,et a1.Estimation of coherent wideband LFM signals based on fractional Fourier domain[C]//Proceedings of the First International Conference on Control(1CICIC'06).Beijing,China:[s.n.],2006,3:18-21.

[5]陶然,齐林,王越.分数阶 Fourier变换的原理与应用[M].北京:清华大学出版,2004.

[6]ZHANG Yanhong,QI Lin,M U Xiaomin,et a1.2-D DOA estimation of wideband LFM signal in fractional Fourier domain[C]//Proceedings of the First International Conference on Innovative Computing,Information and Control(1CICIC'06).Beijing,China:[s.n.],2006,3:6-9.

[7]丁卫安,马远良.虚拟阵列变换法解相干信号M USIC算法研究[J].微波学报,2008,24(2):27-30.DING Weian,M A Yuanliang.Using M USIC algorithm to estimate the DOA of coherent source via virtual array transformation[J].Journal of Microwaves,2008,24(2):27-30.