Neyer-D法用于解除保险距离试验的可行性

刘 刚,陈 众,王 侠,史金锋

(中国华阴兵器试验中心,陕西华阴 714200)

0 引言

同一批引信在出厂后,每发引信在发射时都存在一个事先未知且不可直接观测到的解除保险距离(对于未解除保险的引信,可认为其解除保险距离是一个超过射程的很大的值)。该距离可视为一连续型随机变量,以其总体的分布为概率分布[1],对该总体分布参数进行估计后可得有关引信保险与解除保险性能的某些信息。

目前使用最多的引信解除保险距离试验方法是兰利法,即采用变步长操作程序,可以估计得到50%发火距离及方差,以此作为估计极限发火距离的基础。而Neyer-D最优化法(以下简称Neyer法)是近年来发展起来的一种新方法,比以前所知的任何试验方法都能更有效地决定分布的参数,可获得与标准感度试验一样的精度,而且所需样品数量较少[2]。

从目前掌握的资料来看,尚无关于该方法在引信解除保险距离试验上的应用报道,国内虽有文献对Neyer法进行介绍,但Neyer法的估计精度到底如何,尚无系统可信的研究。本文将进行相关理论分析,并采用蒙特卡罗仿真对不同情况下的均值、标准差、极端概率点估计进行模拟试验研究,对Neyer法用于引信解除保险距离试验进行可行性分析。

1 Neyer法介绍及使用原理

所谓Neyer法是在20世纪80年代末由Barry T.Neyer提出的[3-4],其中心思想是运用最优化设计理论,把试验的安排、数据的处理综合加以考虑,使得试验水平的选择满足Fisher信息量最大化,从而使数据的统计分析具有一些较好的性质。

本文对Neyer法的理论基础不作推导,只引述结论。以正态分布为例,根据最大似然估计的一般理论,分布参数估计量μe和σe的方差和协方差矩阵由下式给出:

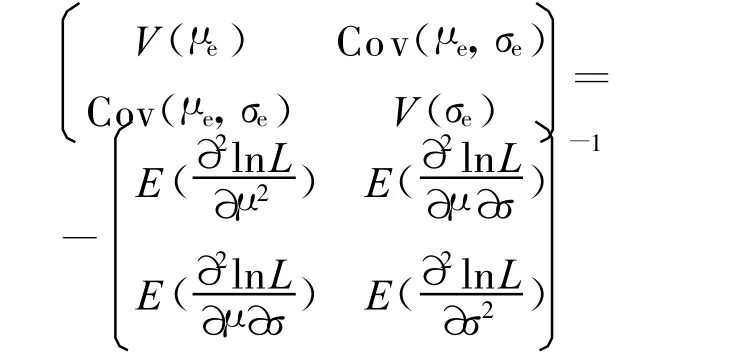
式中,L为似然函数,表达式为:

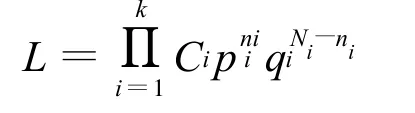
式中,Ci为由Ni和ni所决定的二项式系数,与参数μ、σ无关 。

由于Fisher信息阵正比于参数的方差和协方差矩阵的逆,因此:

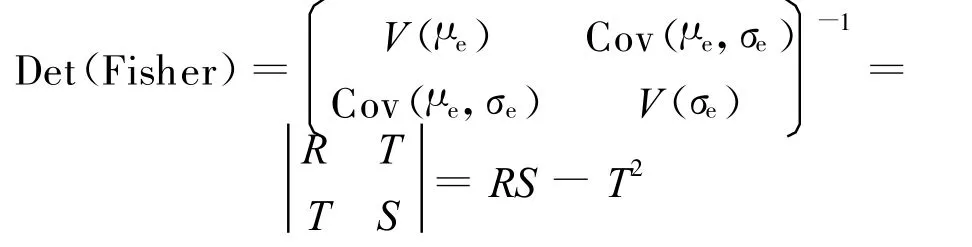
T值较小,可忽略不计,因此Det(Fisher)=RS。Neyer法就是用前面全部的试验结果来计算下一个试验水平,使得当前数据的Det(Fisher),即RS达到最大。

Neyer法的实施程序较兰利法复杂,可参看参考文献[2]。

从以上介绍及有关文献可看出,Neyer法试验水平的选择程序与兰利法、升降法等以往常用感度试验方法区别较大,不再是相对独立的选择过程,而是利用当前的全部试验结果来计算下一个刺激水平,这是该方法的特点同时又是关键点。

应用Neyer法时,需试验者预估3个参数,分别为试验水平的上限、下限和总体标准差的估值。该法产生初期倾向于应用在火工品感度领域,如文献[4]中有关烟火剂感度问题、文献[2]中有关炸药撞击感度问题,均为实例。虽然如此,鉴于火工品感度与引信解除保险距离在本质上近似,方法上相通,因此,具体到本文涉及的引信炮口保险距离试验,3个参数可对应为引信解除保险距离的上限xU、下限xL和解除保险距离标准差σ的估值(记为σguess)。

2 兰利法与Neyer法的蒙特卡罗仿真对比

本文进行的引信解除保险距离试验仿真,建立在如下三条假设的基础上[5]:

1)刺激距离x足够大,引信一定发火;太小,则一定不发火。

3)对于确定的刺激距离x,或者发火,或者不发火,两者必居其一。

根据以上原则,本文编制了相应的仿真程序。

2.1 预估值较准确时的情形

为对比方便起见,对于兰利法和Neyer法,本文同时假设某引信解除保险距离服从N(50,102)的正态分布,试验样本量N分别取15,20,由于两种方法需预估引信解除保险距离的上限xU、下限xL及标准差σguess,为考虑不同的预估情形,在以下不同情况下,均加以计算。

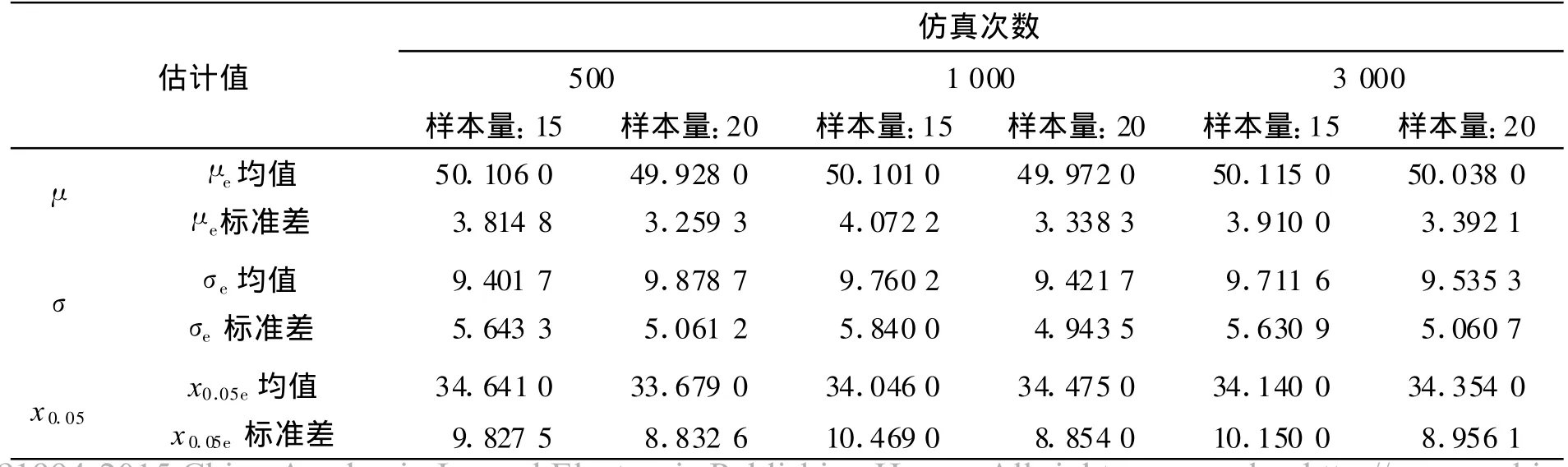
表1 兰利法:xU=80,xL=20Tab.1 Langlie method:xU=80,xL=20

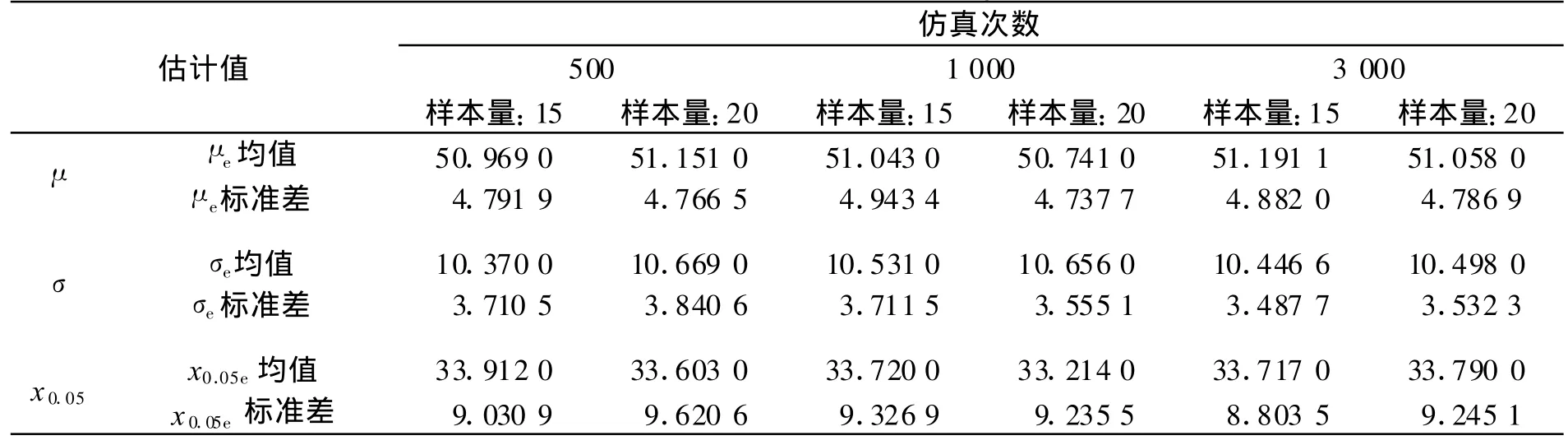
表2 Neyer法:xU=80,xL=20,σguess=σ=10Tab.2 Neyer method:xU=80,xL=20,σguess=σ=10

从表1、表2中可以看出,对于兰利法来说,在距离上下限预估适当的时候,其总体数学期望估计值基本是无偏的,但总体标准差估计是有偏的。而对于Neyer法来说,在距离上下限以及标准差预估值均较为准确的时候,其总体数学期望和标准差估计值都是有偏的,但其偏离程度较小。然而,对于引信解除保险距离来说,实际上最重要的并不是总体数学期望以及标准差的估计,而是某些极端概率点,如5%处的解除保险距离,从表中可以看到,兰利法和Neyer法对于5%处的解除保险距离估计是有明显区别的,如样本量15,仿真3 000次时,Neyer法为33.717,相对于真值33.551,趋近于无偏估计,而兰利法为34.14,明显有偏。因此,从这个角度说,Neyer法要优于兰利法。

2.2 预估值较不准确时的情形

以上的仿真计算结果的前提条件是对引信解除保险距离上下限以及标准差有较准确的预估,该条件在引信设计定型阶段有可能满足,因为有历史数据可供参考,但当引信处于研制初期之时,引信解除保险距离上下限预估值和实际值之间较易产生一定差距,这会对试验结果产生不利影响,因此,考虑预估值不准确时的情形,进行相应的仿真计算。

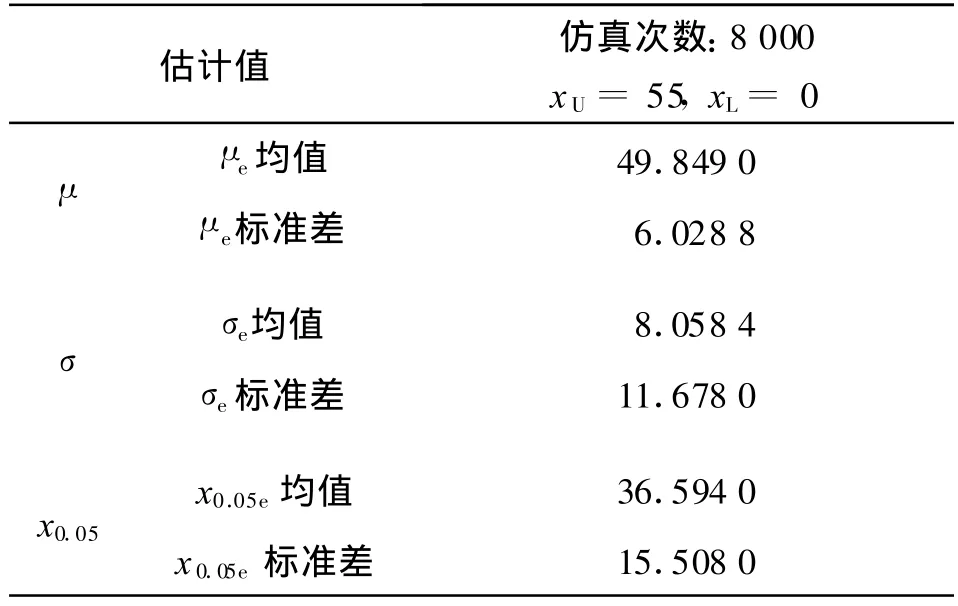
表3 兰利法:N=15Tab.3 Langlie method:N=15

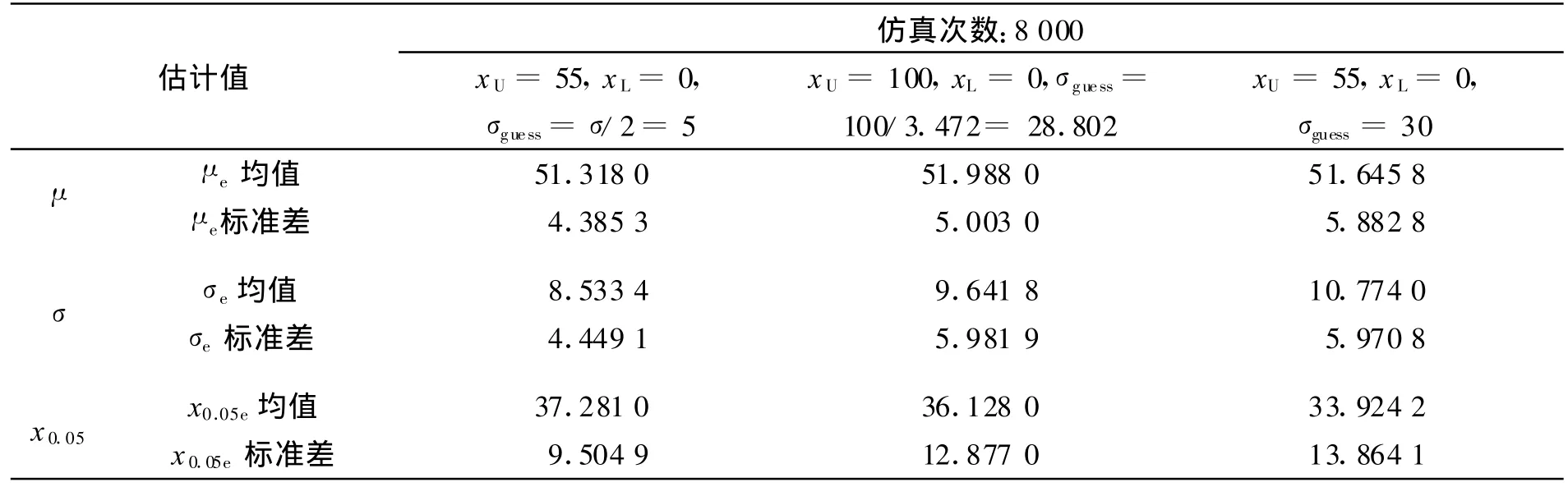
表4 Neyer法:N=15Tab.4 Neyer method:N=15

从表3、表4可看出,当预估值不准确的时候,兰利法和Neyer法对总体数学期望μ的估计μe与预估值准确时的情形相差很小,几乎没有区别,其主要差别体现在对总体标准差的估计σe上,这两种方法的σe都比真值σ有明显偏离,但兰利法偏离的更为严重,其σ标准差远远大于Neyer法。上述情况直接影响了x0.05的估计。容易看出:兰利法和Neyer法的 x0.05e均值差别不大,如 xU=55,xL=0,σguess=5时,Neyer法 x0.05e均值为 37.281,兰利法为36.594,但兰利法的x0.05e标准差要比Neyer法大一些,如前者为 15.508,后者为 9.504 9。因此从实际使用角度来考虑,当预估值不准确时,兰利法对极端概率点 x0.05的估计比Neyer法“散布”更大,更容易得出不准确的结论。

2.3 复杂度分析

从上文的试验原理、仿真分析可看出,相比于兰利法,Neyer法在一些方面占据优势,但同时也增加了复杂度,表现在:

1)刺激水平的计算较为复杂,涉及到Fisher信息阵行列式的最大化问题,须通过计算机才能完成。

2)需要3个预估值,即除了上下限外,还要对总体标准差进行估计,但后者正是试验者想得到的,因此做到准确估计不容易,而一旦上下限与标准差估计同时不准确时,将带来试验结果的较大波动。

3 结论

本文探讨了Neyer-D最优化法应用于引信解除保险距离试验的可行性,分析表明Neyer-D法试验水平的选择与以往常用感度试验方法区别较大,不再是相对独立的选择过程,而是利用当前的全部试验结果来计算下一个刺激水平。蒙特卡罗仿真结果证明,Neyer法对引信极端解除保险概率点的估计更接近于真值,精度更好,体现在:在预估值准确时,其对极端解除保险概率点的估计趋近于无偏;当预估值不准确时,其对极端解除保险概率点估计的标准差小于兰利法。另外,由于试验方法本身原因,Neyer法试验水平的计算比兰利法复杂,同时难以对标准差进行准确估计,影响了试验结果。

Neyer法毕竟还是一种较新的试验方法,在理论基础、试验程序、实际应用情况等方面还处于起步阶段,因此,有必要继续对该方法的发展情况进行跟踪了解,分析研究。

[1]刘宝光.敏感性数据分析与可靠性评定[M].北京:国防工业出版社,1995.

[2]袁俊明,刘玉存.Neyer D-最优化的新感度试验方法研究[J].火工品,2005(2):25-27.YUAN Junming,LIU Yucun.Study on new neyer D-optimal sensitivity[J].INitiators&Pyrotechnics,2005(2):25-27.

[3]Barry T.Neyer A D-optimality-based sensitivity Test[J].Technometrics,1994,36(1):61-70.

[4]Barry T.Neyer.Sensitivity testing and analysis[R].Miamisburg OH:EG&G Mound Applied Technologies,1991.

[5]闻泉,王雨时.引信解除保险距离兰利法试验模拟研究[J].兵工学报,2008,29(7):774-780.WEN Quan,WANG Yushi.Simulation for langlie method test of fuze arming distance[J].Acta Armamentarii,2008,29(7):774-780.