基于预测残差平方和的飞机干扰磁场模型求解

张 坚,林春生,罗 青,龚沈光

(1.海军工程大学兵器工程系,湖北武汉 430033;2.海军92038部队装备处,山东青岛 266041)

0 引言

航空磁性探测广泛应用于考古、矿物勘探和水中磁性目标探测等领域。但是在飞机上对地磁异常场进行测量时,必须对飞机干扰磁场进行补偿。这就需要利用测量数据求解飞机干扰磁场模型系数,使用所求系数计算干扰磁场,最后从测量的总磁场中减去干扰磁场,完成飞机磁补偿。因此,飞机干扰磁场模型的求解是飞机磁补偿中的关键技术。

美国学者Tolles和Lawson在20世纪40年代最早对飞机干扰磁场的数学模型进行了研究,建立了经典的Tolles和Lawson模型[1],但没有给出模型的求解方法。其后,Leliak和Bickel均对该模型进行了改进[2-3],但其求解精度仍然不高。文献[4]和文献[5]分别研究了基于神经网络和截断奇异值分解的飞机干扰磁场模型求解算法。神经网络的计算量较大,收敛速度慢,不适合在实际工程应用中进行实时求解。截断奇异值分解法对奇异值截断位置比较敏感,截断位置不合理会使均方误差迅速增大。同时,这两种方法都没有利用求解结果进行飞机磁补偿实验,其求解效果也就无法从根本上进行检验。

飞机干扰磁场模型属线性回归模型,并且存在较强的复共线性。线性模型求解常用方法有最小二乘估计(LS估计)、截断奇异值分解和岭估计等[6]。截断奇异值分解的不足已在前面提到,LS估计运算量小,但在模型存在复共线性时均方误差会很大。针对上述问题,本文提出了将岭估计的预测残差平方和(PRESS)法引入飞机干扰磁场模型求解。

1 飞机干扰磁场模型与岭估计

1.1 飞机干扰磁场模型

飞机干扰磁场包括恒定磁场、感应磁场和涡流磁场。本文用经典Tolles和Lawson模型来描述飞机干扰磁场,模型坐标系如图1所示。图中,机载磁探设备为坐标原点,地磁场矢量He与X,Y,Z轴的夹角为(X0,Y0,Z0),其方向余弦定义为(cosX0,cosY0,cosZ0)。

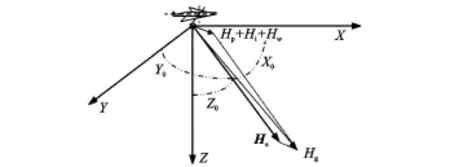
图1 飞机干扰磁场模型坐标系Fig.1 Coordinates of aircraft magnetic interference field model

建模时首先分别建立恒定磁场、感应磁场和涡流磁场的数学模型,将三者叠加后再进行合并与化简,最终可以得到总的飞机干扰磁场ΔH为[1]:

在式(1)两边同时加上地磁场值He后,方程左边就变成了磁场总强度的测量值。利用磁探设备的测量数据和计算出来的方向余弦及其导数,就可以求解式(1)中的16项未知系数,完成飞机干扰磁场模型的参数估计。

1.2 模型复共线性分析

考虑线性回归模型

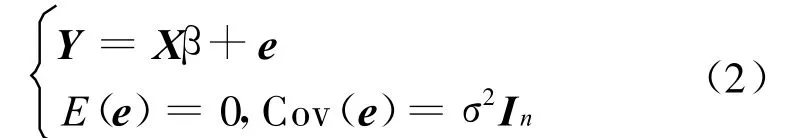
式中,Y为n×1观测向量;X为n×m列满秩设计矩阵,为已知量;β为m ×1待求的模型参数;e为n×1随机误差向量;In为n阶单位阵;σ2为方差参数。

对于飞机干扰磁场模型,X由方向余弦、方向余弦的导数及其乘积项构成,Y由磁场总强度的测量值构成,e为测量误差向量。用LS估计求解模型时均方误差(MSE)很大,原因在于设计矩阵XTX的奇异性。该矩阵产生奇异性的原因是:在保证飞机稳定飞行的情况下,飞机的机动角度不可能很大,这样XTX每一行的对应元素值非常接近,每行之间有比较强的相关性,这就导致飞机干扰磁场模型存在严重的复共线性。

1.3 模型参数的岭估计

为了克服LS估计在模型存在复共线性时的不足,统计学家们提出了许多改进方法,岭估计就是其中一种。岭估计由 Hoerl等人在 1970年首次提出[7],是克服模型复共线性的有效方法。对于线性模型(2),β的岭估计定义为[7]:

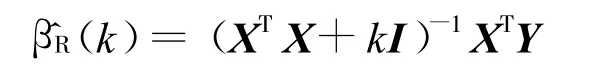
文献[6]提出了基于预测残差平方和(Prediction residual error square sum,PRESS)的岭参数确定方法,其过程如下:

模型(2)中,第 i次观测的数据点为(X1i,X2i,…,),记为 XTi,此时

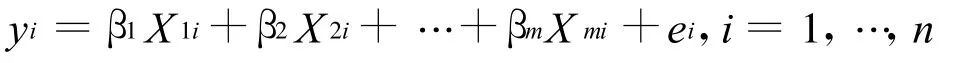
对于这n组数据,如果将第i组数据(Xi,yi)放在一旁,利用其余n-1组数据作线性回归,计算在Xi处的预测值,记为

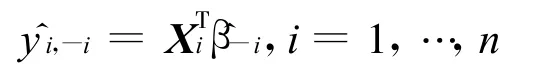
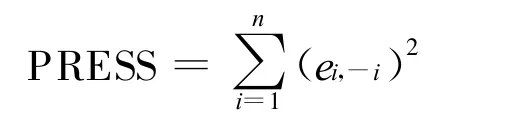
对特定的岭参数k,可以计算出岭估计的PRESS(k),选取使PRESS(k)最小的k值作为岭参数,就得到了最小预测残差平方和意义下的最优岭参数。

2 基于预测残差平方和(PRESS)法的模型求解

本文将PRESS法引入飞机干扰磁场模型求解,并从航空磁性探测的实际应用出发,对PRESS的求解过程作了一定改进。

利用实时采集的n组数据(Xi,yi)(i=1,…,n)作线性回归,预测第 n+1组数据(),将处的预测值记为=。其中,为利用第1到第n组数据求出的回归系数估计值。记=-为第n+1个观测点处的预测残差。同样,利用第2到第n+1组数据来预测第n+2组数据,得到预测残差。对时间序列中连续的L个观测点进行预测,得到预测残差平方和为:

选取最小预测残差平方和意义下的最优岭参数后,采用该岭参数计算飞机干扰磁场模型的岭估计,就完成了模型参数的求解。基于PRESS法的模型求解原理框图如图2所示。

在航空磁性探测的实际应用中,求解模型系数的目的是在后续的飞行过程中,利用所求系数预测飞机干扰磁场的估计值,再从总磁场测量值中减去干扰磁场的估计值,完成飞机磁补偿。其中,为第n+1个观测点处磁场总强度的实际测量值,为利用前n个测量值对其预测的结果。预测残差平方和越小,说明利用所求模型系数计算的干扰磁场与实际干扰磁场越接近,模型求解效果越好,即选用的岭参数k越好。因此,PRESS法符合航空磁性探测的实际物理意义。

图2 基于PRESS法的模型求解原理框图Fig.2 Principle of model solving based on PRESS method

3 模型求解仿真验证

采用Matlab7.0软件仿真验证本文方法在飞机干扰磁场模型求解中的有效性。设地磁场大小为5×104nT。地磁场方向余弦可用地磁场方位角θ和俯仰角φ的函数来表示,且假设dφ/dt=1,dθ/dt=cos(t/2),φ∈ [0,2π],θ∈ [0,π]。观测数据采样点数为576。设定模型系数的真值如下:恒定磁场系数[30,40,80],5个感应磁场系数均为0.005,8个涡流磁场系数均为0.002。利用设定的系数真值,仿真产生飞机干扰磁场信号,如图3所示。

图3 飞机干扰磁场信号仿真Fig.3 Simulation of aircraft magnetic interference field signal

衡量矩阵病态程度的方法之一是求它的条件数。计算得到法矩阵XTX的条件数为2.37×1010,呈严重病态性。采用LS估计和岭估计的计算结果如表1所示,岭估计分别采用岭迹法、GCV法和PRESS法进行k值估计,结果分别为:0.087,不收敛,0.316。采用均方误差(MSE)作为求解效果评判标准。

表1 LS估计和岭估计的计算结果Tab.1 Calculation result of LS estimation and ridge estimation

由表1的计算结果可以得出以下结论:

1)LS估计的均方误差远大于岭估计(除了GCV法不收敛以外),这是由于法矩阵XTX的条件数很大,模型复共线性严重。

2)在本例中,利用GCV法估计k值时,曲线是逐渐衰减的,所以无法确定最小的k值;利用岭迹法估计k值时,需要根据经验来估计,带有主观性。几种方法中PRESS法的均方误差最小,这也验证了该方法符合航空磁性探测应用的实际物理意义。

4 飞机磁补偿实验验证

利用上节LS估计、岭迹法和PRESS法求解出的模型系数,对仿真产生的飞机干扰磁场信号进行磁补偿实验。利用磁偶极子模型生成磁性目标信号如图4所示。将目标信号与飞机干扰磁场叠加后的混合信号如图5(a)所示,可以看出,飞机干扰磁场的变化幅度超过10 nT,目标信号完全被干扰磁场所淹没,无法检测到目标。分别采用LS估计、岭迹法和PRESS法所求系数进行磁补偿后的信号如图5(b)—图5(d)所示。可以看出:LS估计补偿后的信噪比最低,PRESS法的信噪比最高;三种方法中只有PRESS法的补偿结果可以准确检测到目标,其他两种方法都不同程度上会受到噪声的干扰。这也进一步验证了本文方法在飞机磁补偿中的有效性。

图4 磁偶极子目标信号Fig.4 Target signal of magnetic dipole

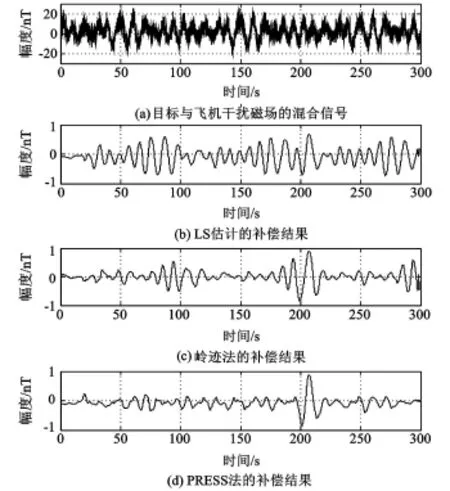
图5 目标与飞机干扰磁场的混合信号及补偿后的结果Fig.5 Mixed signal of target and aircraft magnetic interference field and the result after compensation

5 结论

本文提出了将岭估计的预测残差平方和(PRESS)方法引入飞机干扰磁场模型求解。PRESS法通过计算时间序列的预测残差平方和,选取最小预测残差平方和意义下的最优岭参数。仿真表明:岭估计的均方误差明显小于LS估计,并且PRESS法的均方误差小于岭迹法和GCV法。实验表明:采用PRESS法的岭估计补偿后的信噪比最高,在飞机磁补偿中与其他方法相比具有明显的优越性。

[1]Tolles W E,Lawson J D.Magnetic compensation of MAD equipped aircraft[R].New York:Airborne Instruments Lab Inc,1950.

[2]Leach B W.Aeromagnetic compensation as a linear regression problem[J].Information Linkage Between Applied Mathematics and Industry,1980(2):139-161.

[3]Bickel S H.Small signal compensation of magnetic fields resulting from aircraft maneuvers[J].IEEE T rans on AES,1979,15(4):515-525.

[4]Peter M Williams.Aeromagnetic compensation using neural networks[J].Neural Computing &Applications,1993,(1):207-214.

[5]庞学亮,林春生,张宁.飞机磁场模型系数的截断奇异值分解法估计[J].探测与控制学报,2009,31(5):48-51.PANG Xueliang,LIN Chunsheng,ZHANG Ning.Parameter estimation of airplane magnetic model based on TSVD[J].Journal of Detection&Control,2009,31(5):48-51.

[6]张金槐.线性模型参数估计及其改进[M].第2版.长沙:国防科技大学出版社,1999.

[7]Hoerl A E,Kennard R W.Ridge regression:biased estimation for non-orthogonal problems[J].Technometrics,1970(12):55-88.

[8]叶仁玉,曾建军.特殊数据的广义岭估计的迭代算法及其实现[J].合肥工业大学学报(自然科学版),2007,30(8):1 065-1 068.YE Renyu,ZENG Jianjun.Iterative algorithm of generalized ridge estimates for some special data and its realization[J].Journal of Hefei University of Technology,2007,30(8):1 065-1 068.

[9]刘雁雨,李建伟,刘晓刚.部分岭估计的岭参数确定方法[J].测绘科学技术学报,2007,24(6):413-414.LIU Yanyu,LI Jianwei,LIU Xiaogang.Determination of the partial ridge parameters[J].Journal of Zhengzhou Institute of Surveying and Mapping,2007,24(6):413-414.