浅析如何在高等数学教学中渗透数学建模思想

廖玉怀

【摘要】数学建模是将现实问题转化为数学问题的过程，是解决实际问题常用的方法。将数学建模融入高等数学中，关键是渗透数学建模思想。本文结合高等数学的教学谈谈数学建模思想的渗透。

【关键词】数学建模 应用 渗透

当今的数学已经不仅仅是超脱于一切客观事物的抽象的理论，它渗透到了社会生活的方方面面，成为一种普遍的可以实行的技术。科学技术的发展大大拉近了数学和现实生活的距离。

在高等数学教学中渗透数学建模思想不仅能激发学生学习数学的兴趣，培养学生应用数学知识解决实际问题的能力，还能帮助学生更好地理解和掌握数学中的定义、定理，从而起到事半功倍的效果。本文结合高等数学的教学谈谈数学建模思想的渗透。

一、高等数学中的数学建模思想

把应用数学语言所得到的能反映实际对象的那些数学关系式、图表、数学结构或有效算法的过程称为数学建模。简单地说，所谓数学建模就是用数学的观点去解决实际生活中的问题。数学建模通常很难直接套用现成的结论或模式，但是有一种不变的东西始终在起作用，那就是数学建模思想。完成数学建模过程，学生需要具备良好的数学建模思想。将数学建模融入高等数学，而不是用“数学模型”或“数学实验”课的内容抢占各个高等数学的阵地，关键是渗透数学建模思想。在高等数学教学过程中，应该培养学生用数学建模的观点和思考方式解决复杂的实际问题的能力。

二、把握数学建模嵌入的时机

数学建模在什么时机嵌入是最合适的?当所学的内容与已有的经验联系起来时，这样的学习才是最有效、最有意义、最有价值的，才能最大限度地调动学生的积极性。引进教学的模型时应借助已知的概念、定理，在解决模型的过程中，引出新的定义、定理方法，这个时候，嵌入数学建模的时机是最合适的，效果是最理想的。

例如，在导出定积分的概念时，设计如下教学过程：

实际问题：(1)如何求曲边梯形的面积?(2)如何求变力沿直线所做的功?(3)如何求变速直线运动的路程?

问题提出后引导学生建立模型：

先看问题(1)，如果曲边梯形是梯形(规则的)，那么其面积=1/2(上底+下底)×高。

问题是这里的梯形是曲边梯形(不规则的)，所以上述公式不能用。我们可以这样考虑：把曲边梯形放在直角坐标系中，第三条直线是x轴，曲线是区间[a，b]上的连续非负函数y=f(x)。在区间[a，b]内插入n-1个点，把区间[a，b]分成n个小区间，当所插入的点足够多时，小曲边梯形就可以用小矩形来近似(即小曲边梯形的面积近似等于小矩形的面积)，把所有小矩形的面积加起来就得到大曲边梯形的面积的近似值，要想得到精确的值，就要在区间[a，b]内插入无穷多个点，使每个小区间段的长度都趋于零，这时所有小矩形的面积之和的极限就是所求的曲边梯形的面积。

再看问题(2)、(3)，类似问题(1)的分析，通过分割、近似、求和、取极限转化为一个和式的极限即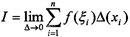，从而抽象出定积分的概念。

三、应用建模思想进行应用问题的教学

(一)灌输数学模型思想，增强学生数学建模意识

所谓数学模型，是指通过抽象和简化，使用数学语言对实际现象的一个近似的刻划，以便于人们更深刻地认识所研究的对象。在高等数学课程中引入数学建模内容的主要目的，是充分利用高等数学课程中丰富的数学建模素材，培养学生的数学模型意识。例如讲函数这一章时，如果仅仅是把它作为中学知识的复习，则单调乏味。如果是从数学模型的观点来看，对实际问题中不同变量之间的联系，建立起函数关系，事实上就是构造相应的数学模型。如，自由落体运动中路程和时间的关系为s=1/2gt²，这就是一个刻划自由落体运动的数学模型。同时指出，构造数学模型往往要忽略一些次要的因素，作一些必要的简化假设，上例中其实隐含了这样一个假设：空气阻力忽略不计。经过这样处理，即向学生灌输了数学模型的概念，又增加了他们学习数学的兴趣，何乐而不为。

(二)运用建模思想分析解决实际应用问题

在课堂教学中，通过对应用题的分析及对教材上已有模型的讲解，介绍数学建模的思想方法，学会从实际问题中筛选有用的信息和数据，建立数学模型，进而提高学生的理解能力、计算能力以及使学生养成精益求精的科学精神，让学生切实感受到数学知识在实际中的应用。

如，根据国家计划生育委员会估计，中国总人口的峰值是2044年，峰值人口数达到15.6亿或15.7亿。如何建立数学模型，合理的论证计生委的估计及如何准确定位、保持人口合理增长?

1.模型基本假设

(1)人口总数的变化是离散型的按整数变化，当总数非常大时，可近似认为人口总数是随时间连续可微地变化；

(2)单位时间内人口增长量与当时的人口成正比例；

(3)设y(t)表示时刻t的人口总数，r为比例系数(即为常数)，且y(t₀)=y₀。

2.建立数学模型

建立数学模型要善于捕捉有效的信息将普通评议转化为数学语言，把实际问题转化为数学问题，进而用数学符号表示之。

根据r为常数的基本假设，t到t+△t时间内人口的增量为：y(t+△t)-y(t)=r·y(t) y(t+△)t

于是，利用微分方程建立起最简单的数学模型：。

3.模型求解

利用分离变量法解此微分方程可得：y=y₀e^r(t-t₀)，这便是著名的马尔萨斯指数增长模型。

4.模型的分析与检验

(1)查相关资料，对照我国计生委、联合国关于地球人口的统计数字与模型计算结果的人口数字作比较，从而检验模型的正确性。

(2)利用模型去考察一下遥远的未来。据统计，地球上的人口按每年2%的速率长着，由此可推算出世界人口总数在2515年将是200万亿，在2625年将是1800万亿，到2660年将是3600万亿。

若按人均地球表面积计算，2625年仅为0.09平方米/人，也就是说必须人挨着人站着才能挤得下；而35年后的2660年，人口又翻了一番，那就是人的肩上再站着人了。随着时间的推移，我们有表明人口将按指数规律无限增长( r>0)。说明此模型的不合理性，这对r为常数的基本假设提出了异议，需要改进。

实际上，高等数学的许多教学内容中都可以引入相应的数学模型，但尽可能选用一些与社会实际生活紧密联系的数学建模案例，使学生感到“数学就在身边”，感到数学有用。使学生不仅掌握理论知识，更重要的是知道怎样应用和自觉去应用数学知识。

四、教学中渗透数学建模思想要注意的几个问题

1.要循序渐进，由简单到复杂，逐步渗透。

2.应选择密切联系学生，易接受、且趣味性、实用的数学建模内容，不能让学生反感。

3.在教学中列举数学建模实例，仅仅是学生学习数学建模的方法和思想的初步，因此，在教学中举例宜少而精，忌大而泛冲淡高等数学理论知识的学习，因为没有扎实的理论知识，也谈不上什么应用。

4.教学中，在强调重视实际应用的同时，要使学生理解和掌握数学理论中所隐含的内在规律性。

五、结束语

在高等数学教学中贯穿数学建模思想，等于教给学生一种好的思想方法，更是给学生一把开启成功大门的钥匙，为学生架起了一座从数学知识到实际问题的桥梁，使学生能灵活地根据实际问题构建出合理的数学模型，得心应手地解决实际问题。

参考文献：

[1]姜启源.数学模型(第三版).高等教育出版社，2003.

[2]刘锋.数学建模.南京大学出版社，2005.

[3]杨桂元.数学模型应用实例.合肥工业大学出版社，2007.